Distribuzione simmetrica

Di Benjamin anderson Agosto 5, 2023 Statistiche 0 commenti

In questo articolo imparerai cosa sono le distribuzioni simmetriche, esempi di distribuzioni simmetriche e come determinare se una distribuzione è simmetrica o asimmetrica.

Cos’è una distribuzione simmetrica?

In statistica, una distribuzione simmetrica è quella che ha lo stesso numero di valori a sinistra della media e a destra della media. In altre parole, in una distribuzione simmetrica, la media è un asse di simmetria.

Ad esempio, la distribuzione normale è una distribuzione simmetrica.

In tutte le distribuzioni simmetriche la media è uguale alla mediana. Ma se anche la distribuzione è unimodale (la modalità statistica è un singolo valore), la media, la mediana e la moda sono equivalenti.

Logicamente, per comprendere appieno cos’è una distribuzione simmetrica, è necessario avere ben chiaro cosa siano media, mediana e moda. Puoi rivedere il significato di questi concetti statistici qui:

➤ Vedi: Cosa sono media, mediana e moda?

Esempi di distribuzioni simmetriche

Considerando la definizione di distribuzione simmetrica, di seguito è riportato un esempio di questo tipo di distribuzione:

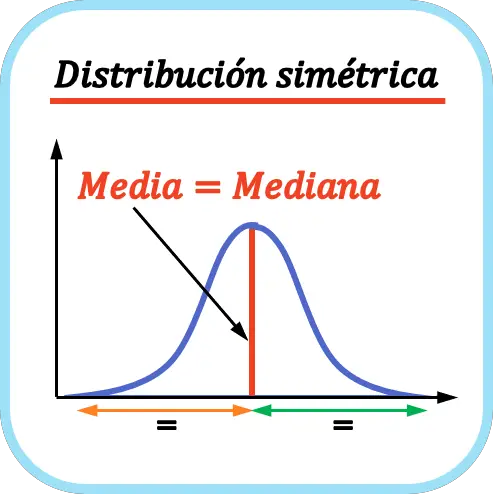
Come mostra il grafico, la distribuzione è simmetrica perché la media si trova proprio al centro di tutti i dati, ovvero la coda a sinistra della curva è uguale alla coda a destra. In questo caso media, mediana e moda coincidono perché la moda è unimodale.

Due chiari esempi di due diversi tipi di distribuzioni di probabilità simmetriche sono la distribuzione normale e la distribuzione uniforme, perché hanno lo stesso numero di valori a sinistra e a destra della media.

D’altra parte, una distribuzione può anche essere simmetrica e bimodale, cioè avere due modalità. Guarda il seguente esempio:

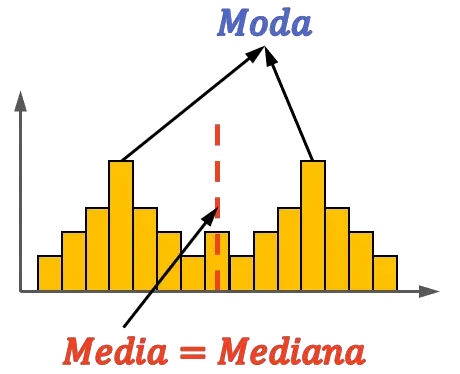
Come puoi vedere in quest’altro esempio, una distribuzione bimodale può anche essere simmetrica, perché può avere la media e la mediana al centro indipendentemente dagli altri valori. Tuttavia, in questo caso la moda non deve necessariamente essere uguale alla media e alla moda.

Altri tipi di distribuzioni in base alla loro simmetria

Oltre alle distribuzioni simmetriche, esistono altri due tipi di distribuzioni asimmetriche.

Distribuzione simmetrica : la distribuzione ha lo stesso numero di valori a sinistra e a destra della media.
Distribuzione positivamente distorta : la distribuzione ha più valori diversi a destra della media che a sinistra.
Distribuzione distorta negativamente : la distribuzione ha più valori diversi a sinistra della media che a destra.

Come capire se una distribuzione è simmetrica

Per determinare se una distribuzione è simmetrica o meno, dobbiamo calcolare il coefficiente di asimmetria di Pearson, la cui formula è:

$A_p=\cfrac{\mu-Mo}{\sigma}$

Oro

$A_p$

è il coefficiente di Pearson,

$\mu$

la media aritmetica,

$Mo$

la modalità (statistiche) e

$\sigma$

la deviazione standard.

Pertanto, a seconda del segno del coefficiente di asimmetria di Pearson, la distribuzione sarà simmetrica o asimmetrica:

Se il coefficiente di asimmetria di Pearson è positivo, significa che la distribuzione è positivamente asimmetrica.
Se il coefficiente di asimmetria di Pearson è negativo, significa che la distribuzione è asimmetrica negativamente.
Se il coefficiente di asimmetria di Pearson è zero, significa che la distribuzione è simmetrica.

Tuttavia il coefficiente di Pearson può essere calcolato solo se la distribuzione è unimodale, altrimenti è necessario utilizzare il coefficiente di asimmetria di Fisher, la cui formula è la seguente:

$\displaystyle\gamma_1=\frac{\displaystyle \sum_{i=1}^N\left(x_i-\mu\right)^3}{N\cdot \sigma ^3}$

Oro

$\mu$

la media aritmetica,

$\sigma$

la deviazione standard e

$N$

il numero totale di dati.

L’interpretazione del coefficiente di asimmetria di Fisher è identica al coefficiente di Pearson: se è positivo significa che la distribuzione è positivamente asimmetrica, se è negativo la distribuzione è negativamente asimmetrica e se è zero significa che la distribuzione è simmetrica.

Informazioni sull'autore

Benjamin anderson

Ciao, sono Benjamin, un professore di statistica in pensione diventato insegnante dedicato di Statorials. Con una vasta esperienza e competenza nel campo della statistica, sono ansioso di condividere le mie conoscenze per potenziare gli studenti attraverso Statorials. Scopri di più