Un'introduzione alla distribuzione uniforme

La distribuzione uniforme è una distribuzione di probabilità in cui ciascun valore compreso in un intervallo da a a b ha la stessa probabilità di verificarsi.

Se una variabile casuale X segue una distribuzione uniforme, allora la probabilità che X assuma un valore compreso tra x ₁ e x ₂ può essere trovata dalla seguente formula:

P(x ₁ < X < x ₂ ) = (x ₂ – x ₁ ) / (b – a)

Oro:

• x ₁ : il valore dell’interesse inferiore
• x ₂ : il valore superiore di interesse
• a: il valore minimo possibile
• b: il valore massimo possibile

Ad esempio, supponiamo che il peso dei delfini sia equamente distribuito tra 100 e 150 libbre.

Se selezioniamo un delfino a caso, possiamo usare la formula sopra per determinare la probabilità che il delfino scelto pesi tra 120 e 130 libbre:

• P(120 < X < 130) = (130 – 120) / (150 – 100)
• P(120 < X < 130) = 10/50
• P(120 < X < 130) = 0,2

La probabilità che il delfino scelto pesi tra 120 e 130 libbre è 0,2 .

Visualizza la distribuzione uniforme

Se creiamo un grafico della densità per visualizzare la distribuzione uniforme, sarebbe simile al grafico seguente:

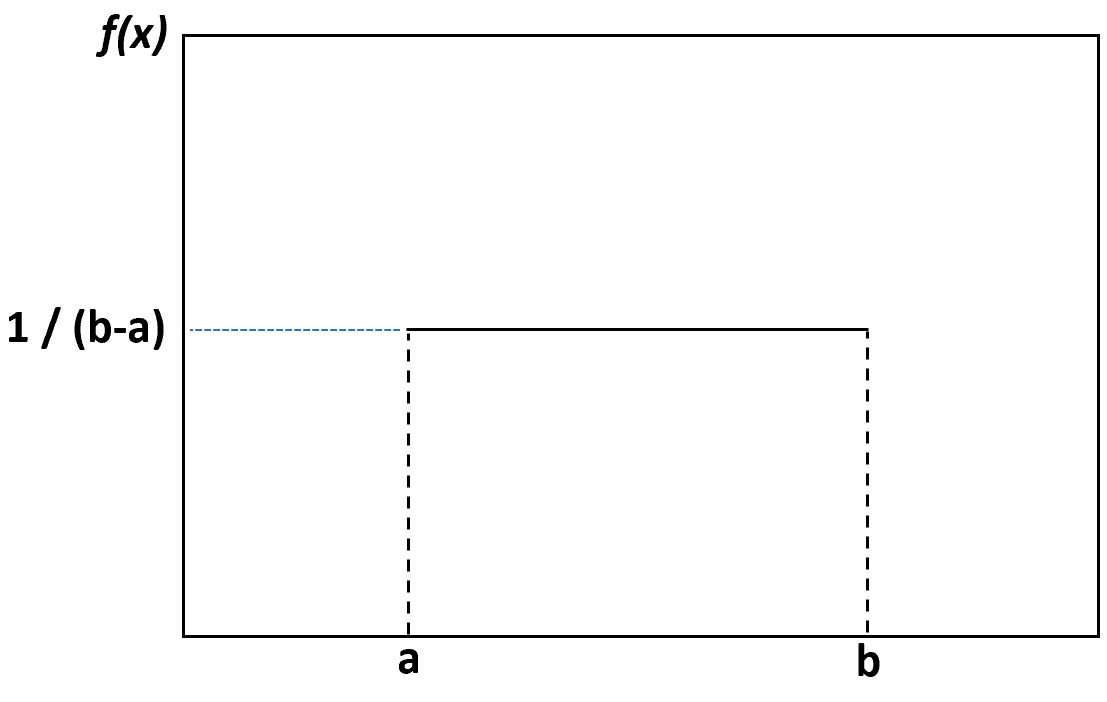
Ogni valore compreso tra il limite inferiore a e il limite superiore b ha la stessa probabilità di verificarsi e qualsiasi valore al di fuori di questi limiti ha una probabilità pari a zero.

Ad esempio, nel nostro esempio precedente, abbiamo detto che il peso dei delfini è equamente distribuito tra 100 e 150 libbre. Ecco come visualizzare questa distribuzione:

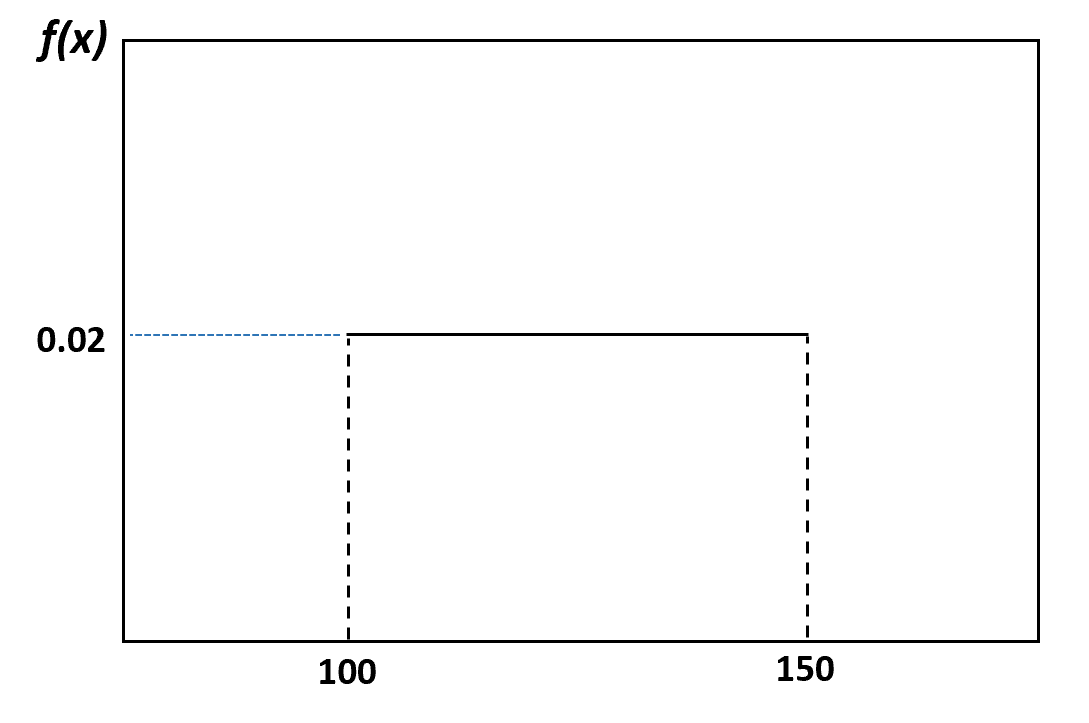
E la probabilità che un delfino selezionato casualmente pesi tra 120 e 130 libbre può essere visualizzata come segue:

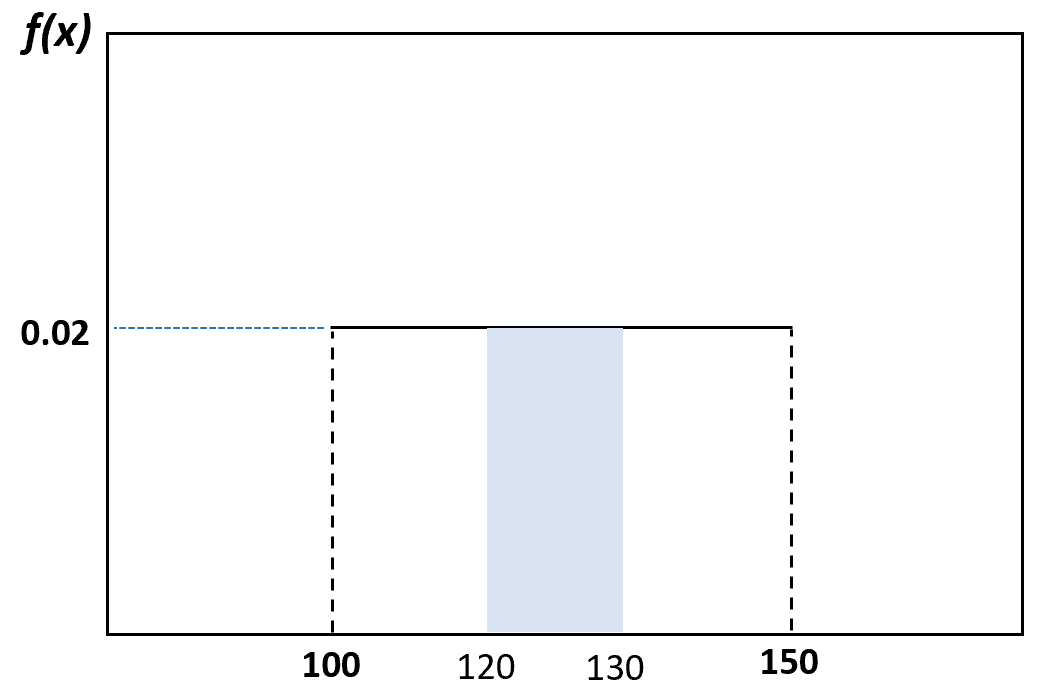
Proprietà della distribuzione uniforme

La distribuzione uniforme ha le seguenti proprietà:

• Media: (a + b) / 2
• Mediana: (a + b) / 2
• Deviazione standard: √ (b – a) ² / 12
• Differenza: (b – a) ² / 12

Ad esempio, supponiamo che il peso dei delfini sia equamente distribuito tra 100 e 150 libbre.

Potremmo calcolare le seguenti proprietà per questa distribuzione:

• Peso medio: (a + b) / 2 = (150 + 100) / 2 = 125
• Peso medio: (a + b) / 2 = (150 + 100) / 2 = 125
• Deviazione standard del peso: √ (150 – 100) ² / 12 = 14,43
• Variazione di peso: (150 – 100) ² / 12 = 208,33

Problemi con le pratiche di distribuzione uniforme

Utilizza i seguenti problemi pratici per verificare la tua conoscenza della distribuzione uniforme.

Domanda 1: Un autobus arriva alla fermata ogni 20 minuti. Se arrivi alla fermata dell’autobus, qual è la probabilità che l’autobus arrivi in 8 minuti o meno?

Soluzione 1: il tempo di attesa minimo è 0 minuti e il tempo di attesa massimo è 20 minuti. Il valore di interesse inferiore è 0 minuti e il valore di interesse superiore è 8 minuti.

Quindi, calcoleremo la probabilità come segue:

P(0 < X < 8) = (8-0) / (20-0) = 8/20 = 0,4 .

Domanda 2: La durata di una partita NBA è equamente distribuita tra 120 e 170 minuti. Qual è la probabilità che una partita NBA selezionata casualmente duri più di 155 minuti?

Soluzione 2: la durata minima è 120 minuti e la durata massima è 170 minuti. Il valore di interesse inferiore è di 155 minuti e il valore di interesse superiore è di 170 minuti.

Quindi, calcoleremo la probabilità come segue:

P(155 < X < 170) = (170-155) / (170-120) = 15/50 = 0,3 .

Domanda 3: Il peso di una certa specie di rana è equamente distribuito tra 15 e 25 grammi. Se scegli una rana a caso, qual è la probabilità che pesi tra 17 e 19 grammi?

Soluzione 3: il peso minimo è di 15 grammi e il peso massimo è di 25 grammi. Il valore di interesse inferiore è di 17 grammi e il valore di interesse superiore è di 19 grammi.

Quindi, calcoleremo la probabilità come segue:

P(17 < X < 19) = (19-17) / (25-15) = 2/10 = 0,2 .

Nota: possiamo utilizzare il calcolatore della distribuzione uniforme per verificare le nostre risposte a ciascuno di questi problemi.