Cos'è una distribuzione unimodale? (definizione & #038; esempio)

Una distribuzione unimodale è una distribuzione di probabilità con un picco evidente.

Ciò contrasta con una distribuzione bimodale , che presenta due picchi netti:

Ciò contrasta anche con una distribuzione multimodale , che presenta due o più picchi:

Nota: una distribuzione bimodale è solo un tipo specifico di distribuzione multimodale.

Esempi di distribuzioni unimodali

Ecco alcuni esempi di distribuzioni unimodali nella pratica.

Esempio 1: peso alla nascita dei bambini

È noto che la distribuzione del peso dei neonati segue una distribuzione unimodale con una media intorno ai 7,5 chili. Se creiamo un istogramma del peso dei bambini, vedremo un “picco” a 7,5 libbre, con alcuni bambini che pesano di più e altri che pesano di meno.

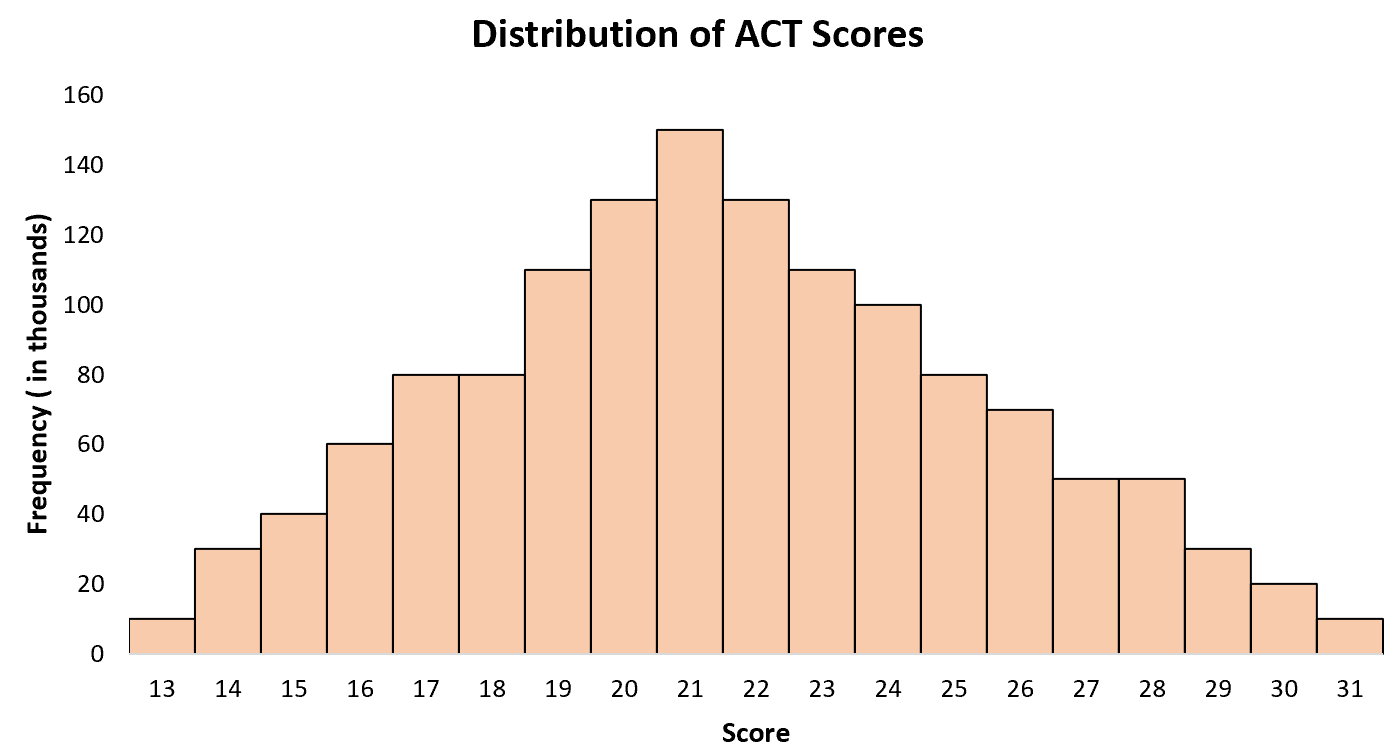
Esempio 2: punteggi ACT

Il punteggio ACT medio per gli studenti delle scuole superiori negli Stati Uniti è di circa 21, con alcuni studenti che ottengono punteggi più bassi e altri che ottengono punteggi più alti. Se creiamo un istogramma dei punteggi ACT per tutti gli studenti negli Stati Uniti, vedremo un unico “picco” all’età di 21 anni, con punteggi più alti per alcuni studenti e punteggi più bassi per altri.

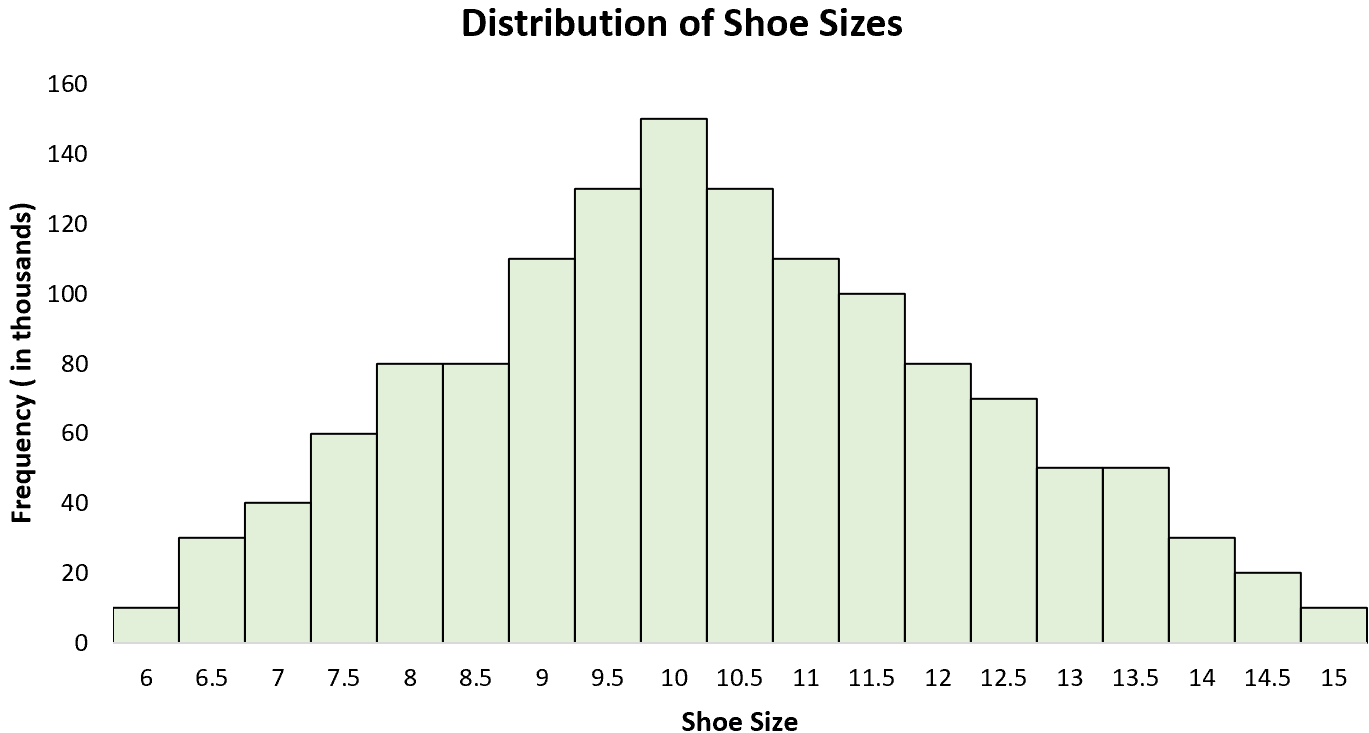
Esempio 3: taglie di scarpe

La distribuzione delle misure delle scarpe da uomo è una distribuzione unimodale con un “picco” intorno a 10. Se creiamo un istogramma di tutte le misure delle scarpe da uomo, vedremo un unico picco a 10 con alcuni uomini che indossano una misura di scarpe più grande e altri che indossano una misura più grande. misurare. taglia più piccola.

Distribuzioni unimodali in statistica

Le seguenti distribuzioni di probabilità nelle statistiche sono tutte distribuzioni unimodali:

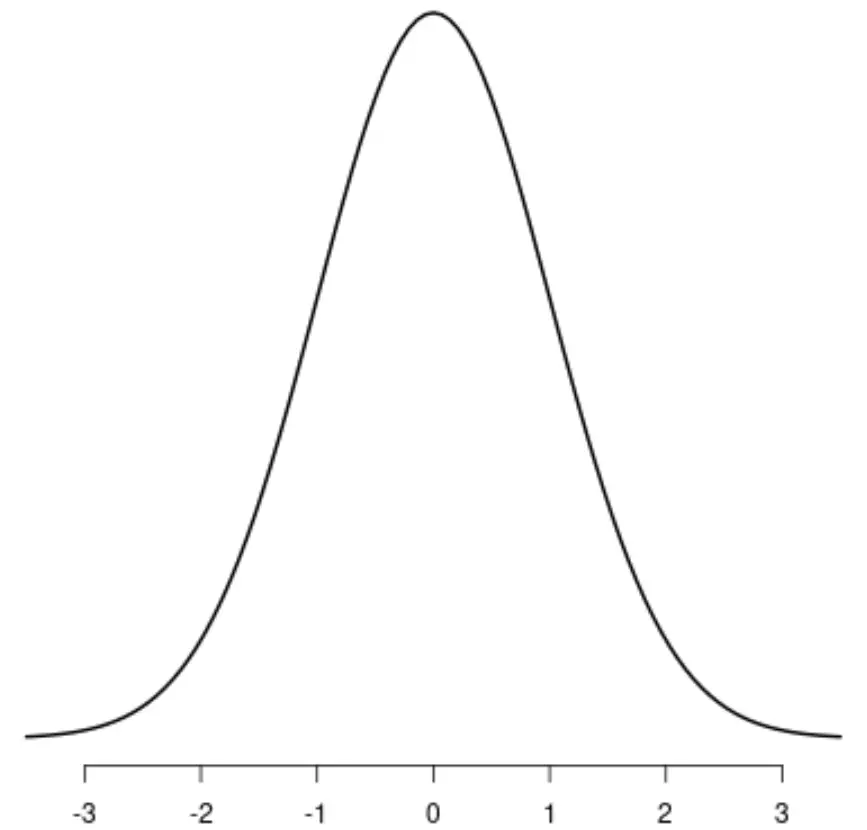
La distribuzione normale

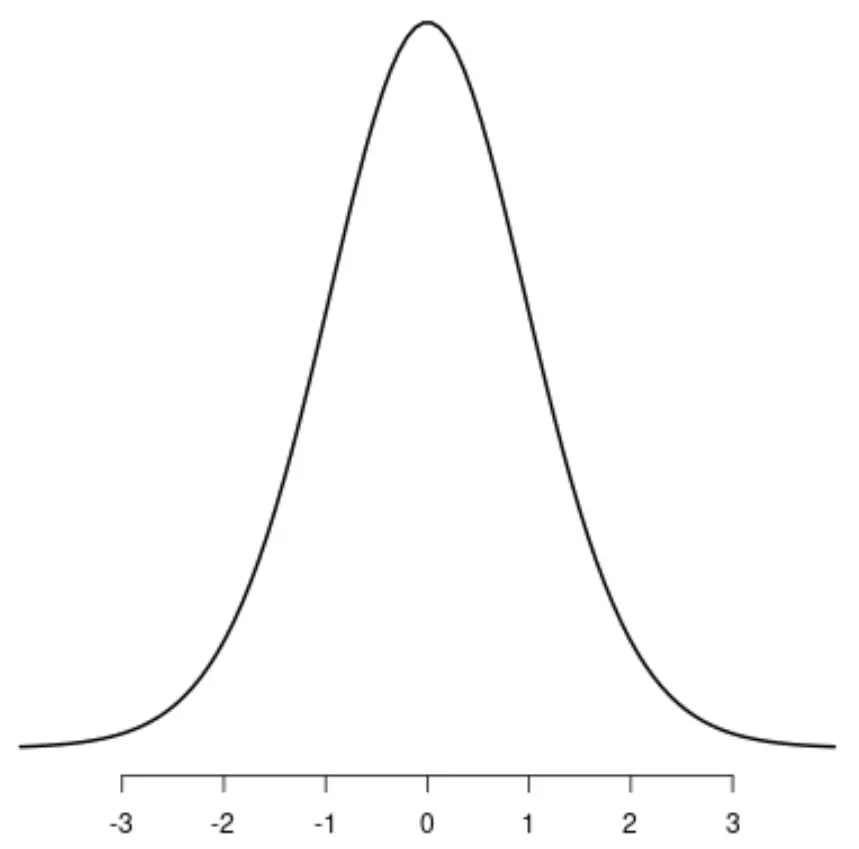
La distribuzione t

Distribuzione uniforme

La distribuzione di Cauchy

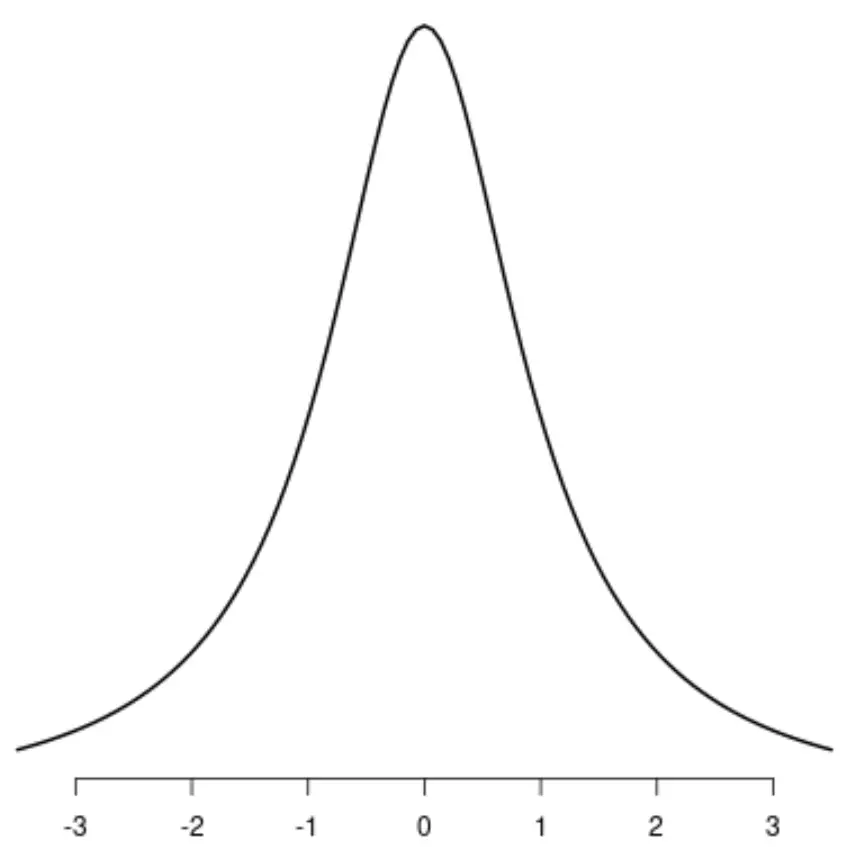
Si noti che ciascuna di queste distribuzioni ha un unico picco distinto.

Come analizzare le distribuzioni unimodali

Spesso descriviamo le distribuzioni unimodali utilizzando tre diverse misure di tendenza centrale :

• Media : il valore medio
• Mediana : il valore mediano
• Moda : il valore che appare più spesso

A seconda dell’asimmetria della distribuzione, queste tre misurazioni possono essere trovate in luoghi diversi.

Distribuzione distorta a sinistra: media <mediana <modalità

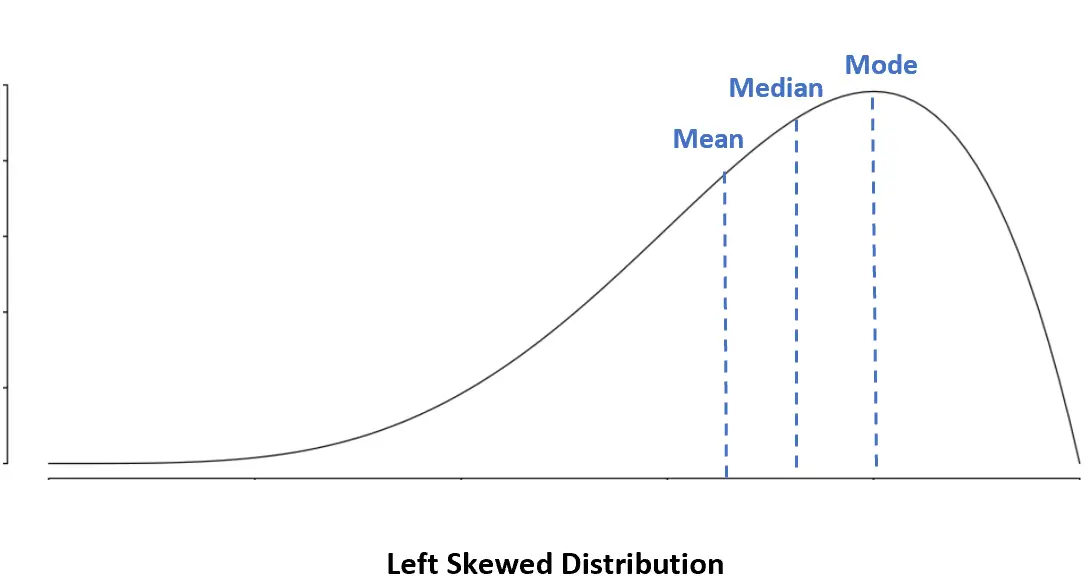
In una distribuzione distorta a sinistra, la media è inferiore alla mediana.

Distribuzione distorta a destra: Modalità < Mediana < Media

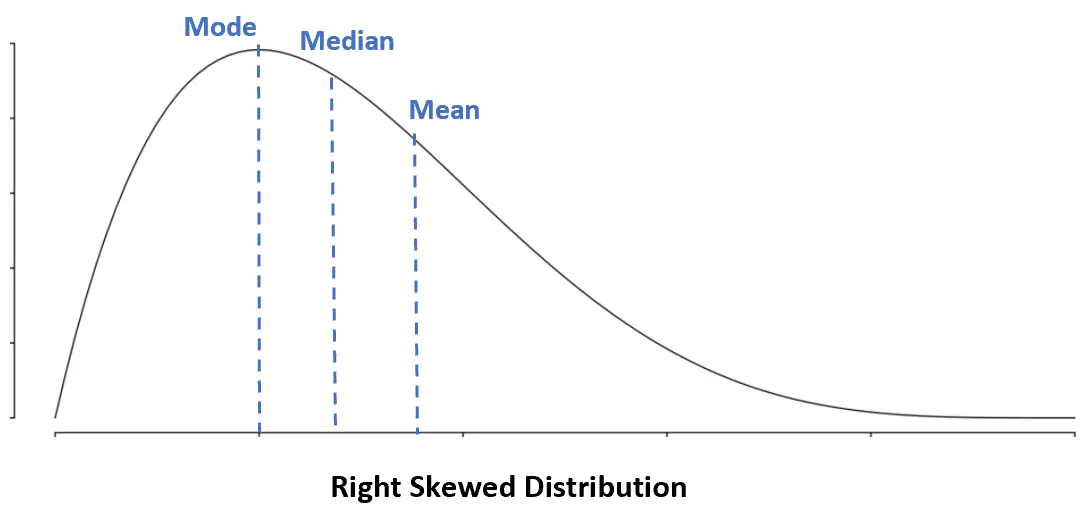
In una distribuzione distorta a destra, la media è maggiore della mediana.

Nessuna distorsione: media = mediana = moda

In una distribuzione simmetrica media, mediana e moda sono tutte uguali.

Risorse addizionali

Distribuzioni distorte a sinistra o a destra
Distribuzioni simmetriche: definizione + esempi