Come eseguire un test t a due campioni in excel
Un t-test a due campioni viene utilizzato per verificare se le medie di due popolazioni sono uguali o meno.
Questo tutorial spiega come eseguire un test t a due campioni in Excel.
Come eseguire un test t a due campioni in Excel
Supponiamo che i ricercatori vogliano sapere se due diverse specie di piante in un dato paese hanno la stessa altezza media. Poiché sarebbe stato troppo lungo andare in giro e misurare ogni pianta, hanno deciso di prelevare un campione di 20 piante di ciascuna specie.
L’immagine seguente mostra l’altezza (in pollici) di ciascuna pianta in ciascun campione:
Possiamo eseguire un t-test a due campioni per determinare se le due specie hanno la stessa altezza media seguendo questi passaggi:
Passaggio 1: determinare se le varianze della popolazione sono uguali .
Quando eseguiamo un t-test su due campioni, dobbiamo prima decidere se assumeremo che le due popolazioni abbiano varianze uguali o disuguali. In generale, possiamo assumere che le popolazioni abbiano varianze uguali se il rapporto tra la varianza campionaria più grande e quella più piccola è inferiore a 4:1.
Possiamo trovare la varianza per ciascun campione utilizzando la funzione Excel =VAR.S(Cell range) , come mostrato nell’immagine seguente:
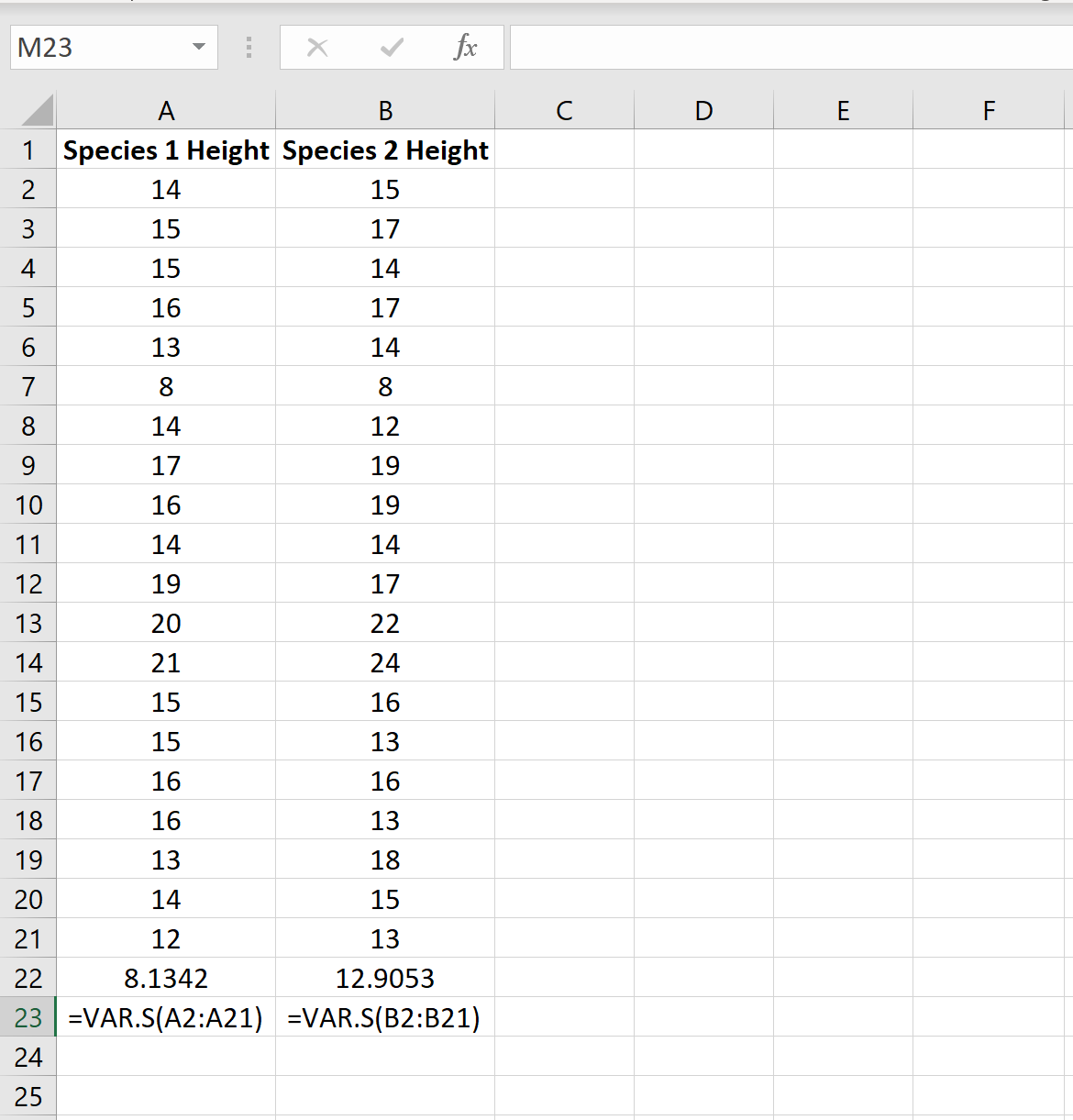
Il rapporto tra la varianza campionaria più grande e la varianza campionaria più piccola è 12.9053/8.1342 = 1.586 , che è inferiore a 4. Ciò significa che possiamo supporre che le varianze della popolazione siano uguali.
Passaggio 2: aprire il ToolPak di analisi .
Nella scheda Dati della barra multifunzione in alto, fai clic su “Analisi dei dati”.
Se non vedi questa opzione da cliccare, devi prima scaricare Analysis ToolPak , che è completamente gratuito.
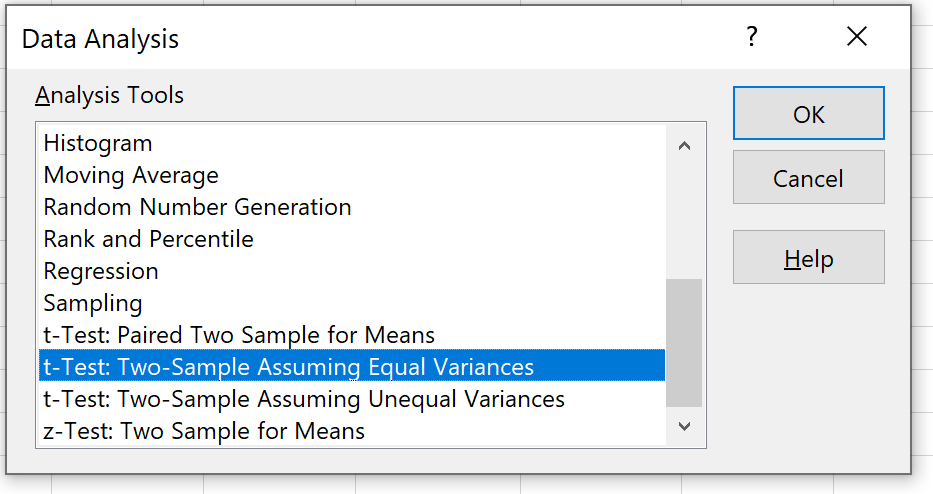
Passaggio 3: selezionare il test appropriato da utilizzare.
Selezionare l’opzione che dice t-test: due campioni assumendo varianze uguali , quindi fare clic su OK.
Passaggio 4: inserisci le informazioni necessarie .
Inserisci l’intervallo di valori per la variabile 1 (il nostro primo campione), variabile 2 (il nostro secondo campione), ipotetica differenza media (in questo caso mettiamo “0” perché vogliamo sapere se la vera differenza media della popolazione è 0) e l’intervallo di output in cui vorremmo vedere visualizzati i risultati del t-test. Quindi fare clic su OK.
Passaggio 5: interpretare i risultati .
Dopo aver fatto clic su OK nel passaggio precedente, verranno visualizzati i risultati del t-test.
Ecco come interpretare i risultati:
Media: questa è la media di ciascun campione. Il campione 1 ha un’altezza media di 15,15 e il campione 2 ha un’altezza media di 15,8 .
Varianza: questa è la varianza per ciascun campione. Il campione 1 ha una varianza di 8,13 e il campione 2 ha una varianza di 12,90 .
Osservazioni: questo è il numero di osservazioni in ciascun campione. Entrambi i campioni contengono 20 osservazioni (ad esempio 20 piante individuali in ciascun campione).
Varianza aggregata: numero calcolato “raggruppando” le varianze di ciascun campione utilizzando la formula s 2 p = [ (n 1 -1)s 2 1 + (n 2 -1)s 2 2 ] / (n 1 +n 2 – 2), che risulta essere 10.51974 . Questo numero viene quindi utilizzato per calcolare la statistica t -test.
Differenza media ipotetica: il numero su cui “ipotizziamo” è la differenza tra le medie delle due popolazioni. In questo caso abbiamo scelto 0 perché vogliamo verificare se la differenza tra le medie delle due popolazioni è uguale o meno a 0, ad esempio se non c’è differenza.
df: i gradi di libertà per il test t, calcolati come n 1 + n 2 -2 = 20 + 20 – 2 = 38 .
t Stat: la statistica del test t , calcolata come t = [ x 1 – x 2 ] / √ [s 2 p (1/n 1 + 1/n 2 )]
In questo caso, t = [15,15-15,8] / √ [10,51974(1/20+1/20)] = -0,63374 .
P(T<=t) a due code: il valore p per un test t a due code. In questo caso, p = 0,530047 . Questo è molto più grande di alfa = 0,05, quindi non riusciamo a rifiutare l’ipotesi nulla. Non abbiamo prove sufficienti per affermare che i mezzi delle due popolazioni siano diversi.
t Critico a due code: questo è il valore critico del test, trovato identificando il valore nella tabella di distribuzione t che corrisponde a un test a due code con alfa = 0,05 e df = 38. Questo risulta essere 2, 024394 . Poiché la nostra statistica del test t è inferiore a questo valore, non riusciamo a rifiutare l’ipotesi nulla. Non abbiamo prove sufficienti per affermare che i mezzi delle due popolazioni siano diversi.
Si noti che l’approccio del valore p e del valore critico porteranno entrambi alla stessa conclusione.
Risorse addizionali
I seguenti tutorial spiegano come eseguire altri tipi di test t in Excel:
Come eseguire un test t per un campione in Excel
Come eseguire un test t per campioni accoppiati in Excel
Informazioni sull'autore
Benjamin anderson
Ciao, sono Benjamin, un professore di statistica in pensione diventato insegnante dedicato di Statorials. Con una vasta esperienza e competenza nel campo della statistica, sono ansioso di condividere le mie conoscenze per potenziare gli studenti attraverso Statorials. Scopri di più