Come risolvere: errore in xy.coords(x, y, xlabel, ylabel, log): le lunghezze "x" e "y" differiscono

Un errore comune che potresti riscontrare in R è:

 Error in xy.coords(x, y, xlabel, ylabel, log): 
  'x' and 'y' lengths differ 

Questo errore si verifica quando si tenta di creare un grafico di due variabili ma le variabili non hanno la stessa lunghezza.

Questo tutorial spiega esattamente come correggere questo errore.

Come riprodurre l’errore

Supponiamo di provare a creare un grafico a dispersione delle seguenti due variabili in R:

 #define x and y variables
x <- c(2, 5, 5, 8)
y <- c(22, 28, 32, 35, 40, 41)

#attempt to create scatterplot of x vs. y
plot(x, y)

Error in xy.coords(x, y, xlabel, ylabel, log): 
  'x' and 'y' lengths differ

Riceviamo un errore perché le lunghezze di xey non sono uguali.

Possiamo confermarlo stampando la lunghezza di ciascuna variabile:

 #print length of x
length(x)

[1] 4

#print length of y
length(y)

[1] 6

#check if length of x and y are equal
length(x) == length(y)

[1] FALSE

Come correggere l’errore

Il modo più semplice per correggere questo errore è semplicemente assicurarsi che i due vettori abbiano la stessa lunghezza:

 #define x and y variables to have same length
x <- c(2, 5, 5, 8, 9, 12)
y <- c(22, 28, 32, 35, 40, 41)

#confirm that x and y are the same length
length(x) == length(y)

[1] TRUE

create scatterplot of x vs. y
plot(x, y)

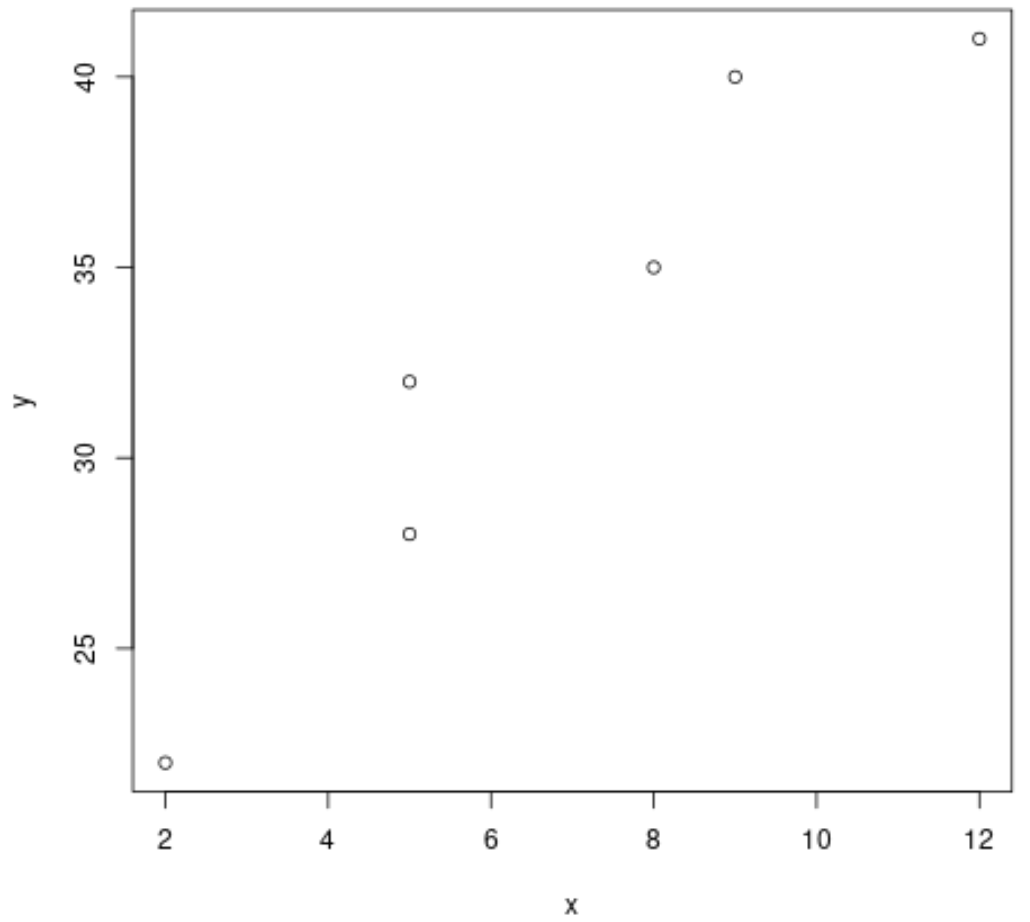
Se un vettore risulta essere più corto dell’altro, puoi scegliere di tracciare solo i valori fino alla lunghezza del vettore più corto.

Ad esempio, se il vettore xa ha 4 valori e il vettore y ha 6 valori, potremmo creare un grafico a dispersione utilizzando solo i primi 4 valori di ciascun vettore:

 #define x and y variables
x <- c(2, 5, 5, 8)
y <- c(22, 28, 32, 35, 40, 41)

#create scatterplot of first 4 pairwise values of x vs. y
plot(x, y[1: length (x)])

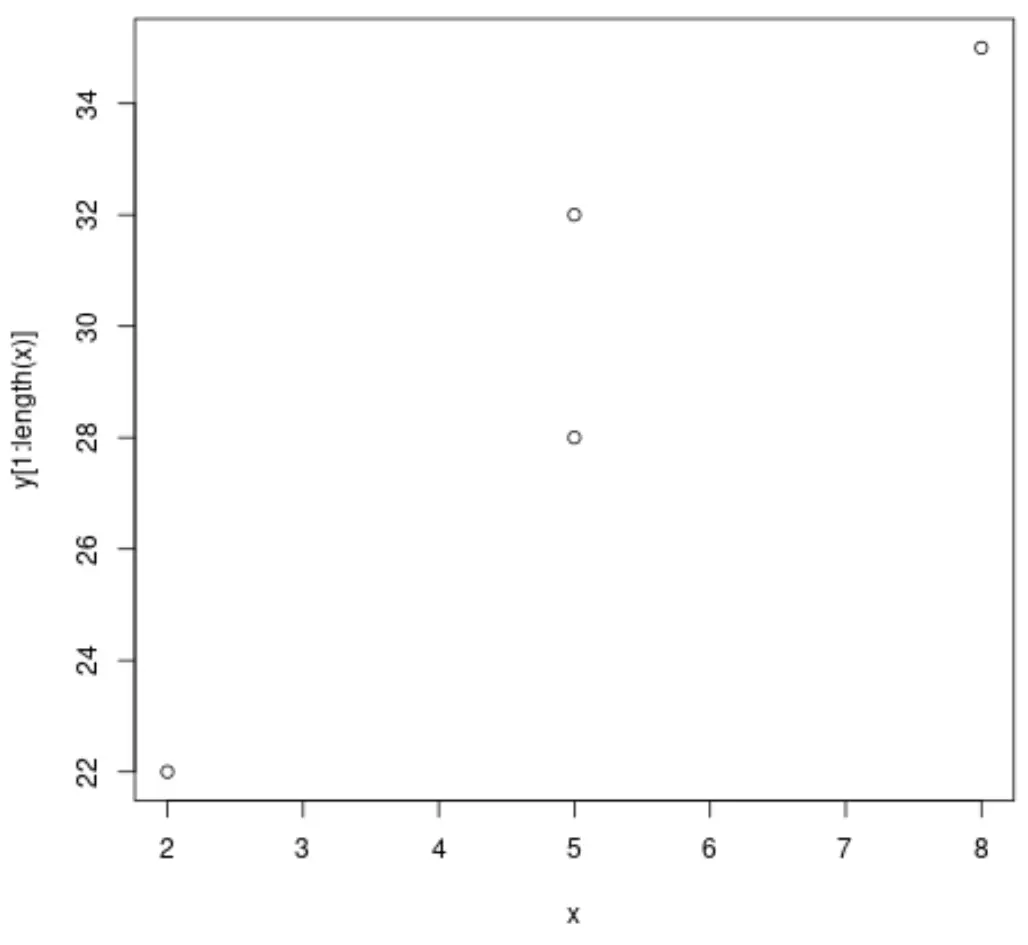
Si noti che solo i primi quattro valori di ciascun vettore vengono utilizzati per creare la nuvola di punti.

Risorse addizionali

Come risolvere in R: NA introdotte dalla coercizione
Come riparare in R: suggerimento fuori limite
Come risolvere il problema: la lunghezza dell’oggetto maggiore non è un multiplo della lunghezza dell’oggetto minore