Come calcolare l'errore quadratico medio (rmse) in excel

In statistica, l’analisi di regressione è una tecnica che utilizziamo per comprendere la relazione tra una variabile predittrice, x, e una variabile di risposta, y.

Quando eseguiamo l’analisi di regressione, otteniamo un modello che ci indica il valore previsto della variabile di risposta in base al valore della variabile predittore.

Un modo per valutare quanto bene il nostro modello si adatta a un determinato set di dati è calcolare l’ errore quadratico medio , che è una metrica che ci dice quanto distano in media i nostri valori previsti dai valori osservati.

La formula per trovare l’errore quadratico medio, più comunemente nota come RMSE , è:

RMSE = √[ Σ(P _i – O _i ) ² / n ]

Oro:

• Σ è un simbolo di fantasia che significa “somma”
• _Pi è il valore previsto per l’ ^iesima osservazione nel set di dati
• O _i è il valore osservato per l’ ^iesima osservazione nel set di dati
• n è la dimensione del campione

Note tecniche :

• L’errore quadratico medio può essere calcolato per qualsiasi tipo di modello che produca valori previsti, che possono poi essere confrontati con i valori osservati di un set di dati.
• L’errore quadratico medio è talvolta chiamato anche deviazione quadratica media, che è spesso abbreviato in RMSD.

Successivamente, esaminiamo un esempio di come calcolare l’errore quadratico medio in Excel.

Come calcolare l’errore quadratico medio in Excel

Non esiste una funzione integrata per calcolare l’RMSE in Excel, ma possiamo calcolarlo abbastanza facilmente con un’unica formula. Mostreremo come calcolare l’RMSE per due diversi scenari.

scenario 1

In uno scenario, puoi avere una colonna contenente i valori previsti dal tuo modello e un’altra colonna contenente i valori osservati. L’immagine seguente mostra un esempio di questo scenario:

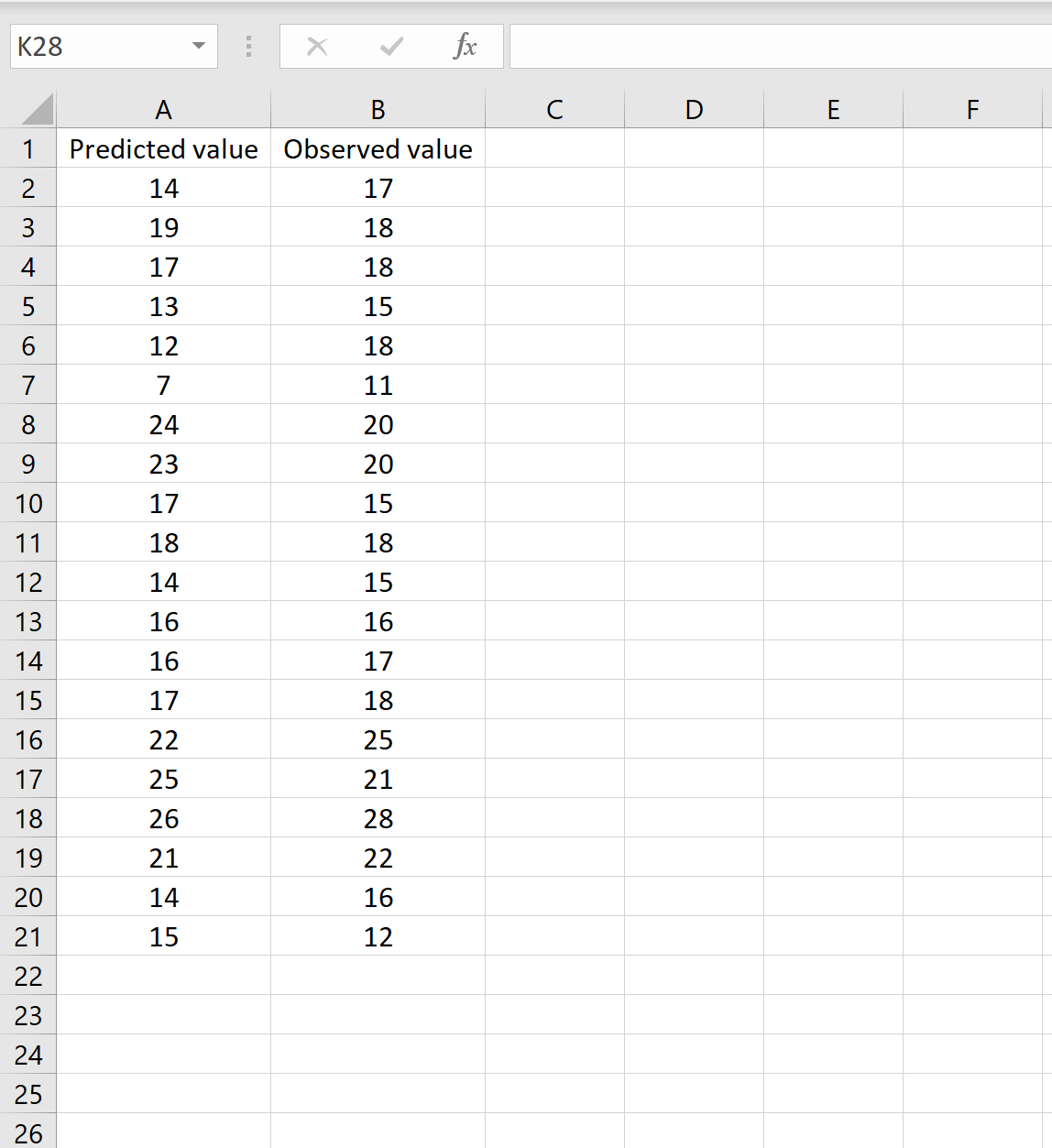
In tal caso, puoi calcolare l’RMSE digitando la seguente formula in qualsiasi cella e quindi facendo clic su CTRL+MAIUSC+INVIO:

=SQRT(SOMMAQ(A2:A21-B2:B21) / CONTEGGIO(A2:A21))

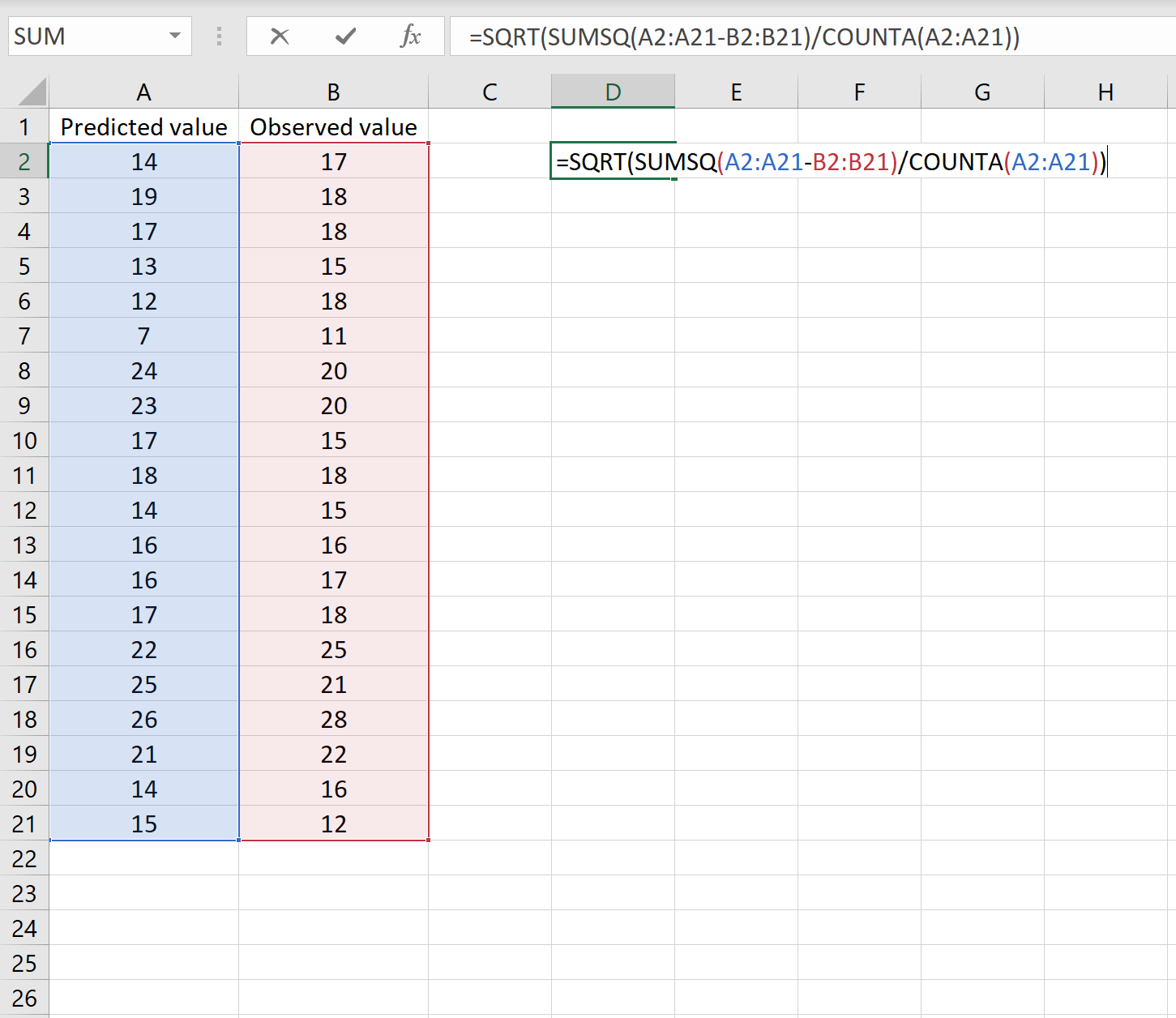
Questo ci dice che l’errore quadratico medio è 2.6646 .

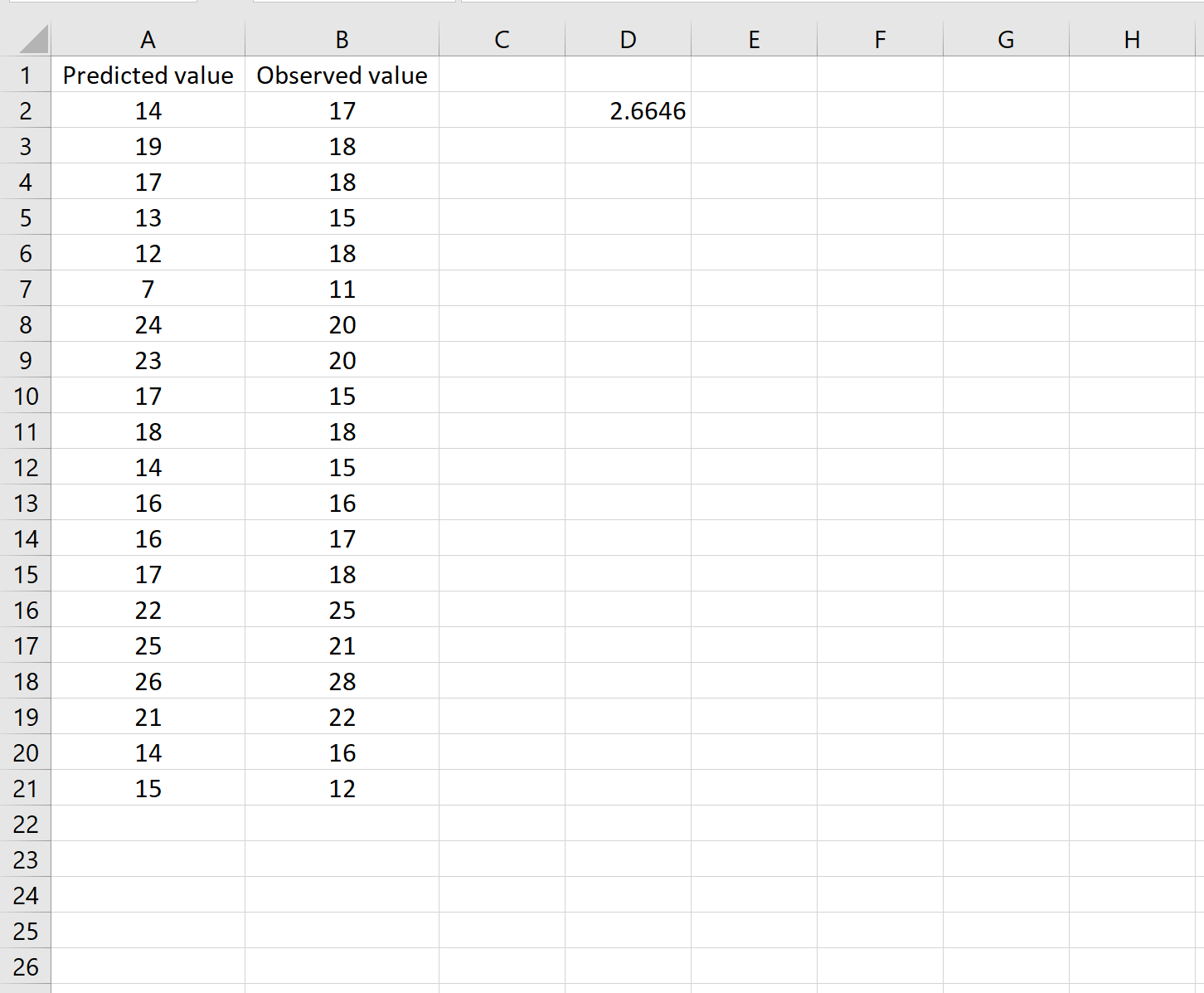
La formula può sembrare un po’ complicata, ma ha senso una volta scomposta:

= TQ.Q( SOMMAQ(A2:A21-B2:B21) / CONTEGGIO(A2:A21) )

• Per prima cosa calcoliamo la somma dei quadrati delle differenze tra i valori previsti e quelli osservati utilizzando la funzione SUMSQ() .
• Successivamente, dividiamo per la dimensione del campione del set di dati utilizzando COUNTA() , che conta il numero di celle in un intervallo che non sono vuote.
• Infine, prendiamo la radice quadrata dell’intero calcolo utilizzando la funzione SQRT() .

Scenario 2

In un altro scenario, potresti aver già calcolato le differenze tra i valori previsti e quelli osservati. In questo caso avrai solo una colonna che mostra le differenze.

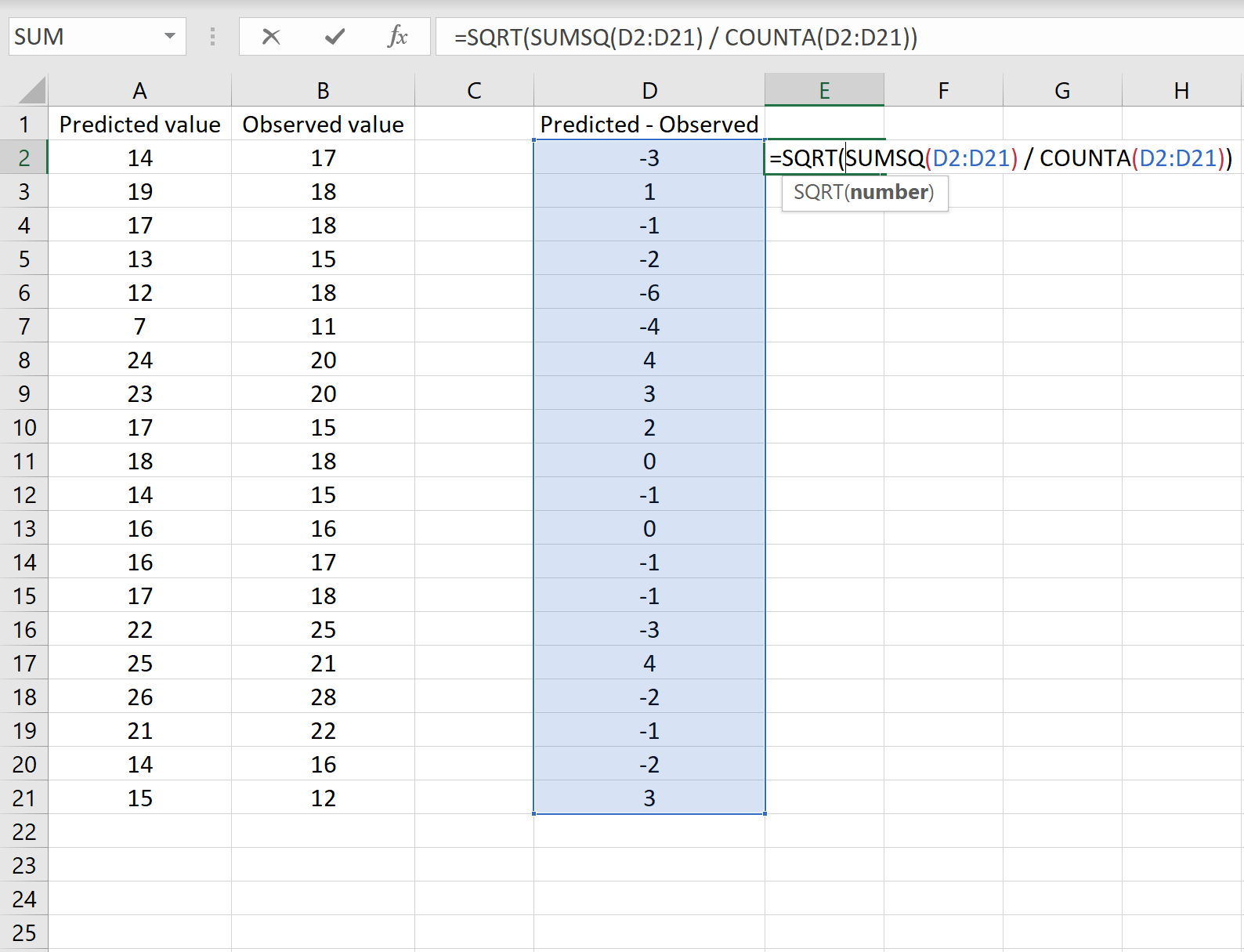
L’immagine seguente mostra un esempio di questo scenario. I valori previsti sono mostrati nella colonna A, i valori osservati nella colonna B e la differenza tra i valori previsti e quelli osservati nella colonna D:

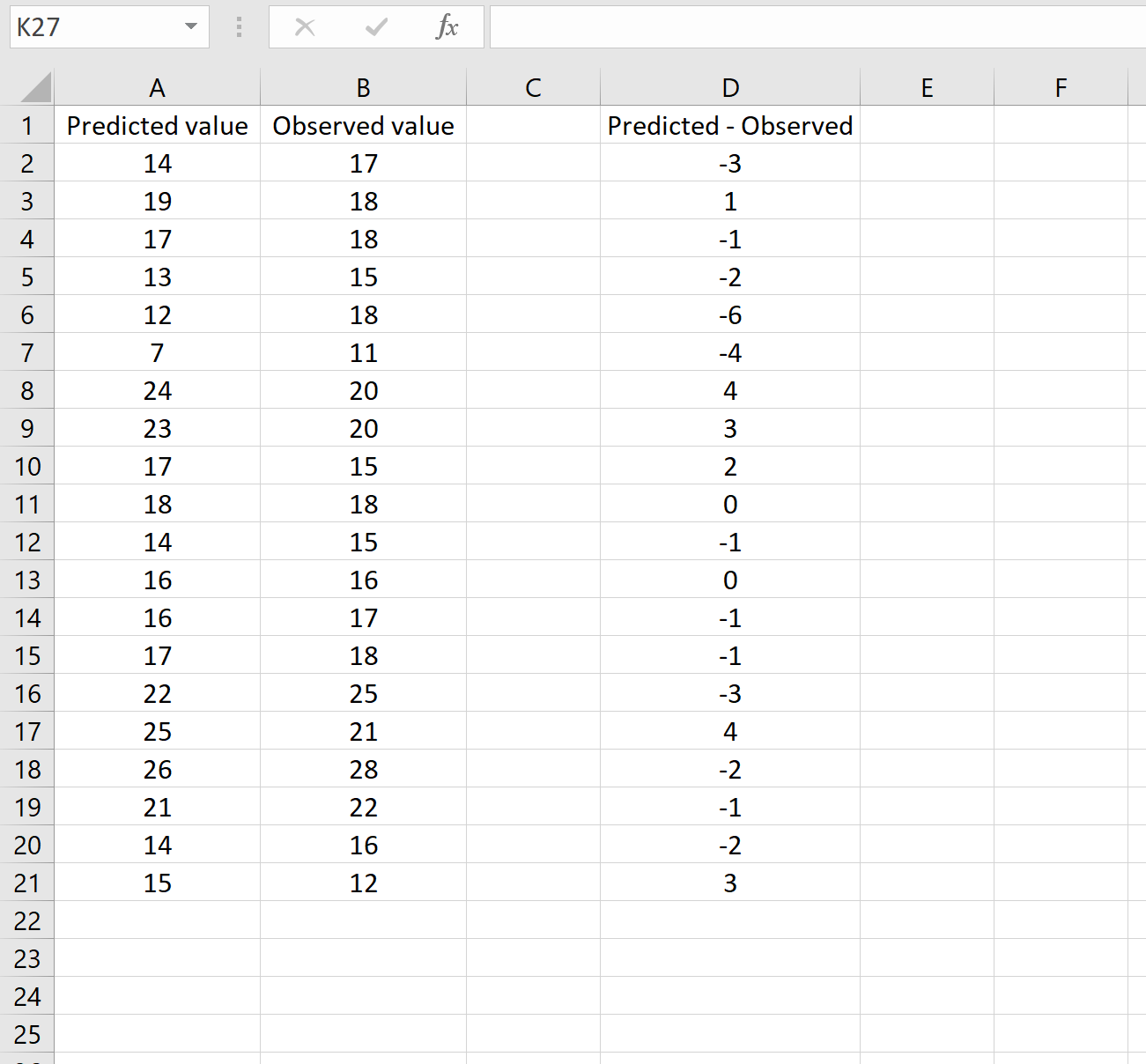
In tal caso, puoi calcolare l’RMSE digitando la seguente formula in qualsiasi cella e quindi facendo clic su CTRL+MAIUSC+INVIO:

=QRT(SOMMAQ(D2:D21) / CONTEGGIO(D2:D21))

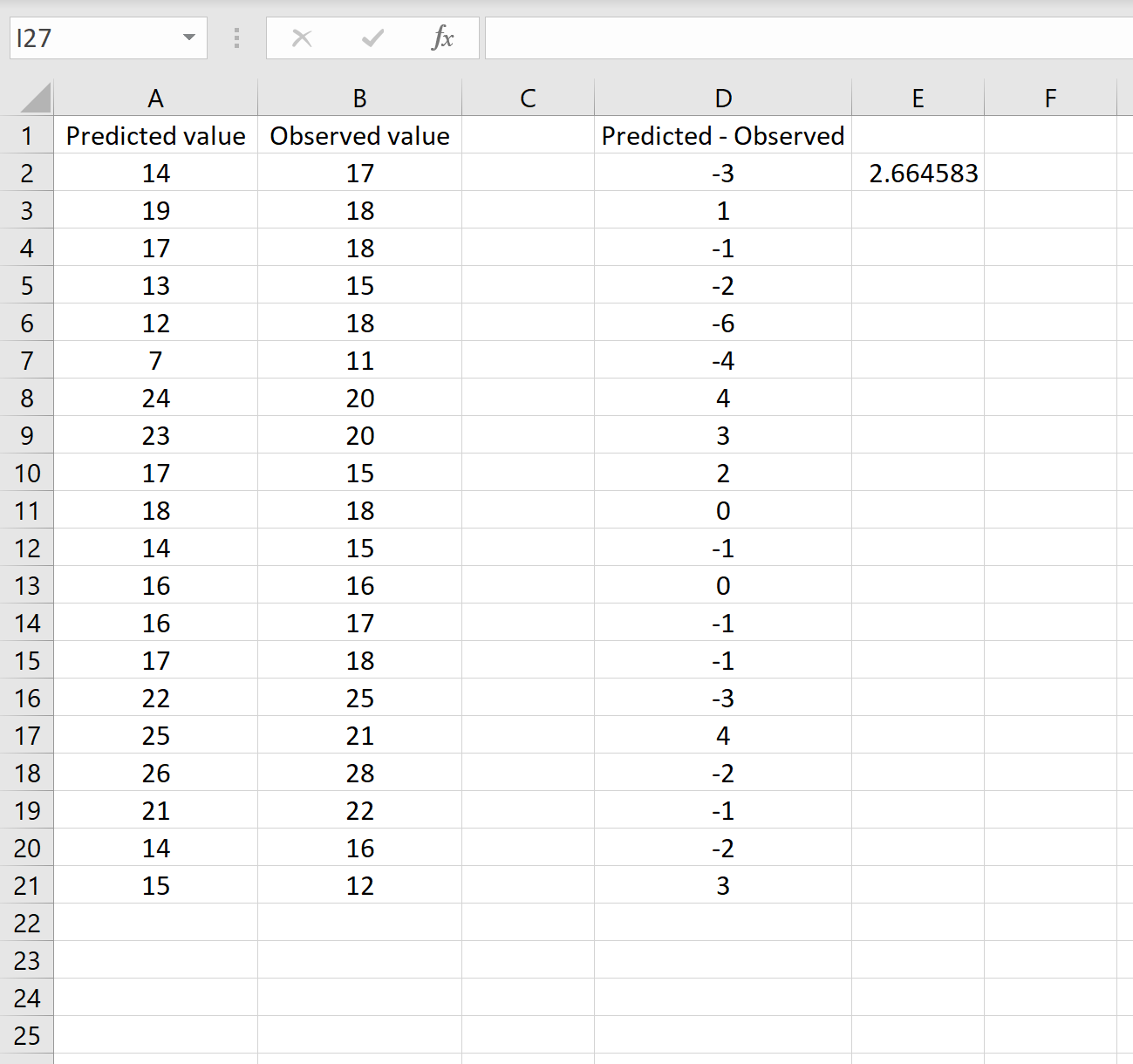
Questo ci dice che l’errore quadratico medio è 2.6646 , che corrisponde al risultato ottenuto nel primo scenario. Ciò conferma che questi due approcci al calcolo dell’RMSE sono equivalenti.

La formula che abbiamo utilizzato in questo scenario è solo leggermente diversa da quella utilizzata nello scenario precedente:

= TQ.Q( SOMMAQ(D2:D21) / CONTEGGIO(D2:D21) )

• Poiché abbiamo già calcolato le differenze tra i valori previsti e quelli osservati nella colonna D, possiamo calcolare la somma dei quadrati delle differenze utilizzando la funzione SUMSQ().   funzione con solo i valori della colonna D.
• Successivamente, dividiamo per la dimensione del campione del set di dati utilizzando COUNTA() , che conta il numero di celle in un intervallo che non sono vuote.
• Infine, prendiamo la radice quadrata dell’intero calcolo utilizzando la funzione SQRT() .

Come interpretare l’RMSE

Come accennato in precedenza, RMSE è un modo utile per vedere quanto bene un modello di regressione (o qualsiasi modello che produce valori previsti) sia in grado di “adattarsi” a un set di dati.

Maggiore è l’RMSE, maggiore è la differenza tra i valori previsti e quelli osservati, il che significa che peggiore è l’adattamento del modello di regressione ai dati. Al contrario, più piccolo è l’RMSE, migliore è la capacità del modello di adattare i dati.

Può essere particolarmente utile confrontare l’RMSE di due diversi modelli per vedere quale modello si adatta meglio ai dati.

Per ulteriori tutorial su Excel, assicurati di consultare la nostra pagina Guide di Excel , che elenca tutti i tutorial di Excel sulle statistiche.