Comprendere l'errore standard di una pendenza di regressione

L’ errore standard della pendenza di regressione è un modo per misurare l'”incertezza” nella stima della pendenza di regressione.

Viene calcolato come segue:

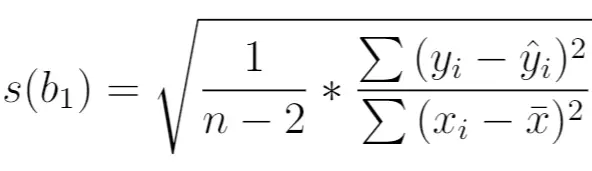
Oro:

• n : dimensione totale del campione
• y _i : valore reale della variabile di risposta
• ŷ _i : valore previsto della variabile di risposta
• x _i : valore reale della variabile predittiva
• x̄ : valore medio della variabile predittiva

Minore è l’errore standard, minore è la variabilità attorno alla stima del coefficiente per la pendenza di regressione.

L’errore standard della pendenza della regressione verrà visualizzato in una colonna “errore standard” nell’output della regressione della maggior parte dei software statistici:

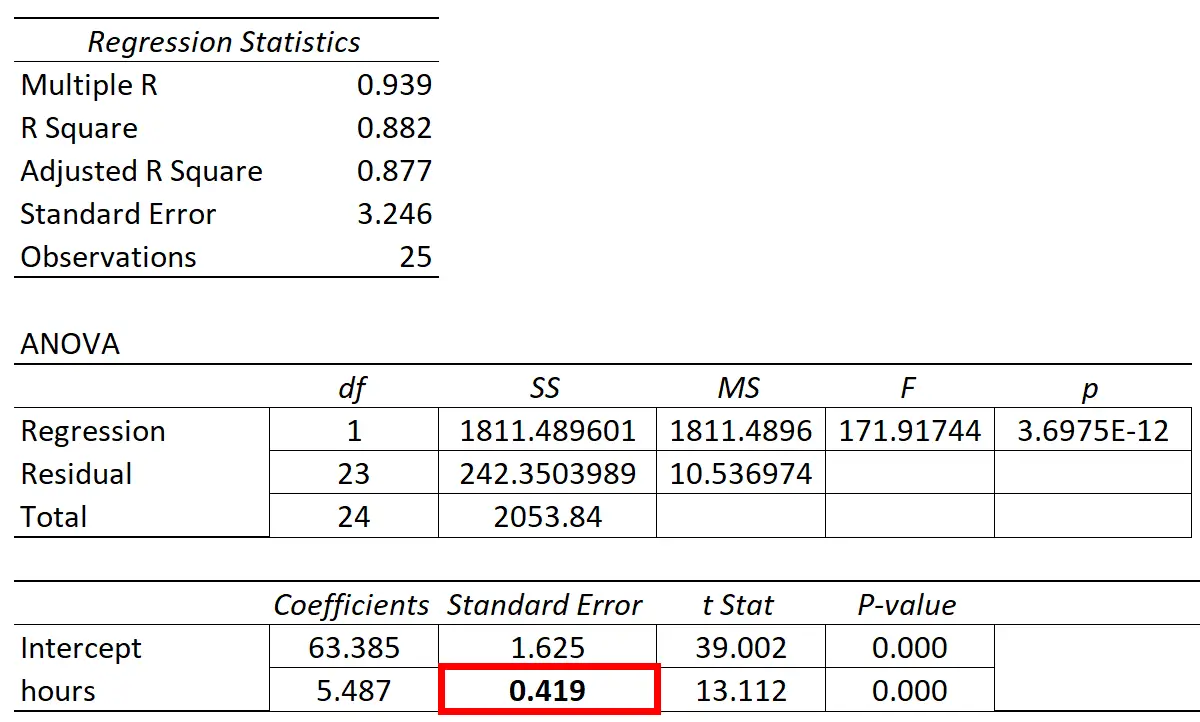
Gli esempi seguenti mostrano come interpretare l’errore standard di una pendenza di regressione in due scenari diversi.

Esempio 1: interpretazione di un piccolo errore standard di una pendenza di regressione

Supponiamo che un professore voglia capire la relazione tra il numero di ore studiate e il voto dell’esame finale degli studenti della sua classe.

Raccoglie dati per 25 studenti e crea il seguente diagramma a dispersione:

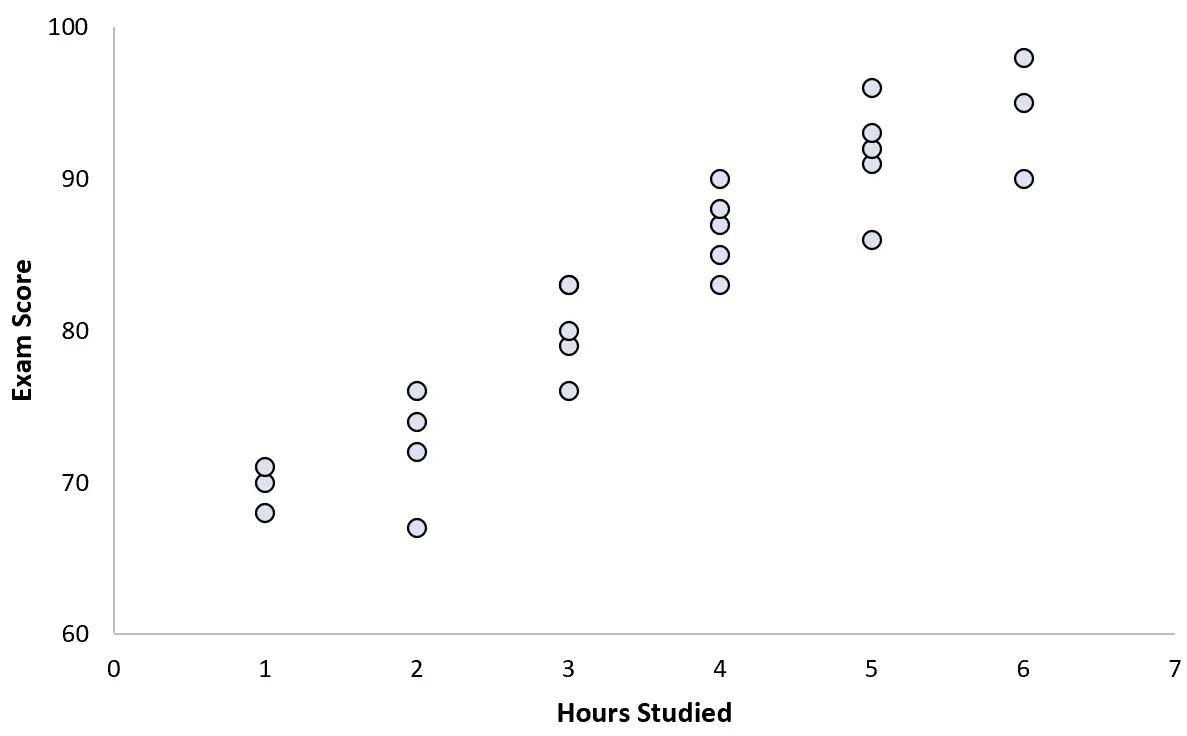
Esiste un’associazione chiaramente positiva tra le due variabili. All’aumentare del numero di ore studiate, il punteggio dell’esame aumenta a un ritmo abbastanza prevedibile.

Ha quindi adattato un semplice modello di regressione lineare utilizzando le ore studiate come variabile predittiva e il voto dell’esame finale come variabile di risposta.

La tabella seguente mostra i risultati della regressione:

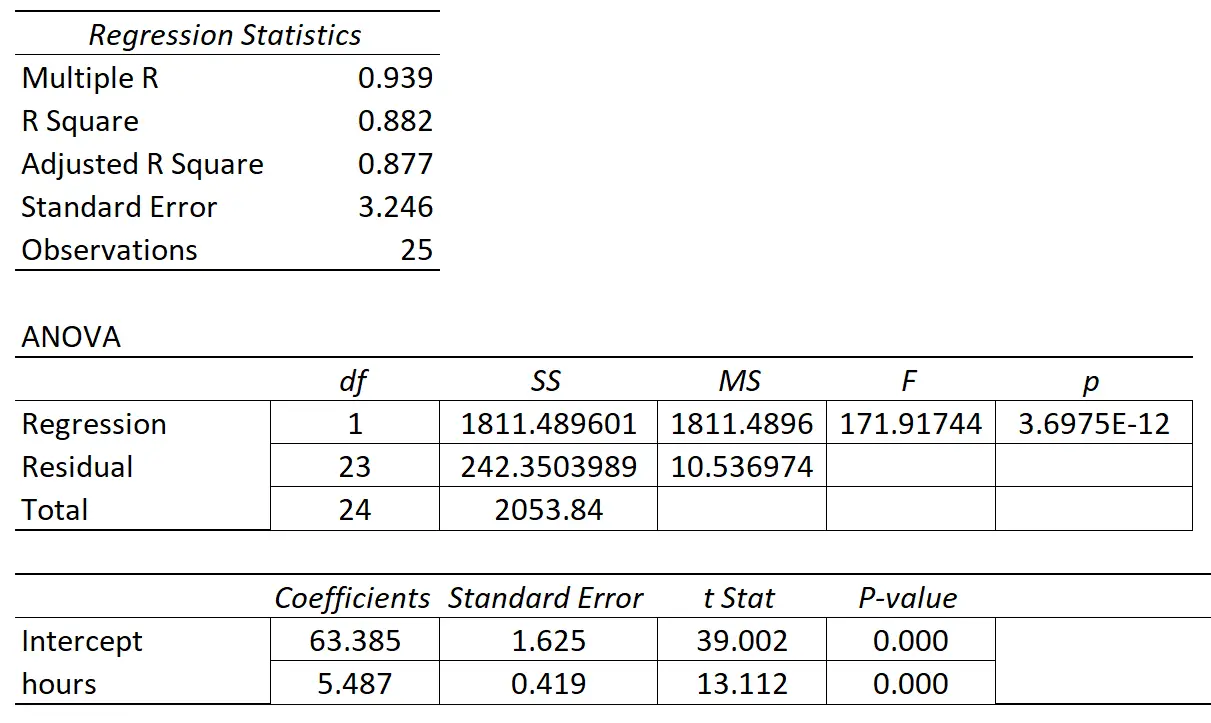
Il coefficiente della variabile predittiva “ore di studio” è 5.487. Questo ci dice che ogni ora aggiuntiva studiata è associata a un aumento medio di 5.487 nel punteggio dell’esame.

L’errore standard è 0,419 , che rappresenta una misura della variabilità attorno a questa stima per la pendenza della regressione.

Possiamo utilizzare questo valore per calcolare la statistica t per la variabile predittiva “ore studiate”:

• statistica t = stima del coefficiente/errore standard
• statistica t = 5,487 / 0,419
• statistica t = 13.112

Il valore p che corrisponde a questa statistica del test è 0,000, il che indica che le “ore studiate” hanno una relazione statisticamente significativa con il voto dell’esame finale.

Poiché l’errore standard della pendenza di regressione era piccolo rispetto alla stima del coefficiente della pendenza di regressione, la variabile predittrice era statisticamente significativa.

Esempio 2: interpretazione di un errore standard ampio di una pendenza di regressione

Supponiamo che un altro professore voglia capire la relazione tra il numero di ore studiate e il voto dell’esame finale degli studenti della sua classe.

Raccoglie dati per 25 studenti e crea il seguente diagramma a dispersione:

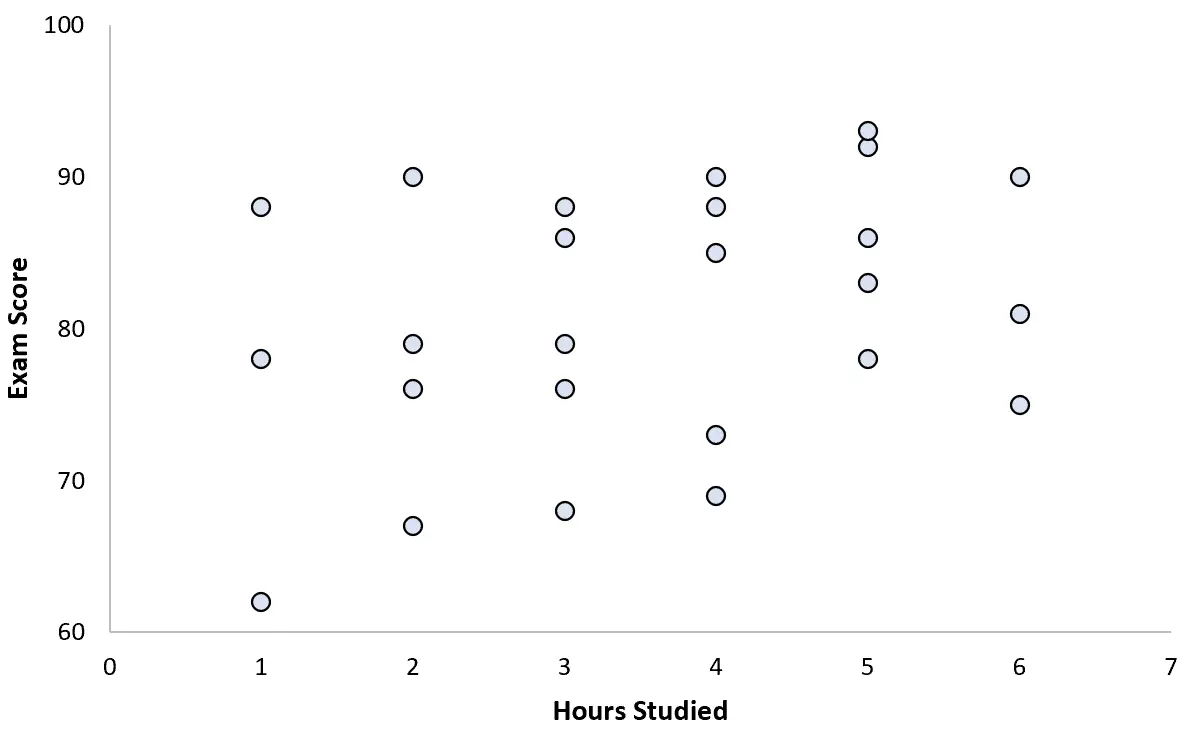
Sembra esserci una leggera associazione positiva tra le due variabili. All’aumentare del numero di ore di studio, il punteggio dell’esame generalmente aumenta, ma non ad un ritmo prevedibile.

Supponiamo che il professore adatti quindi un semplice modello di regressione lineare utilizzando le ore studiate come variabile predittiva e il voto dell’esame finale come variabile di risposta.

La tabella seguente mostra i risultati della regressione:

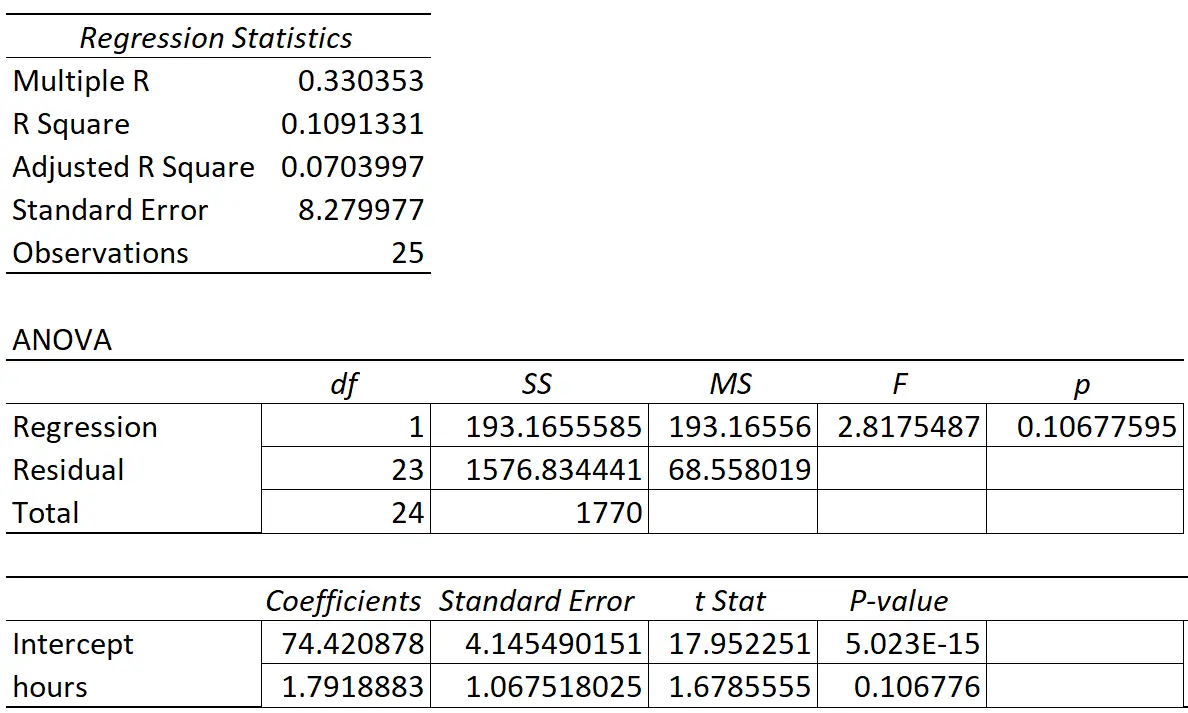
Il coefficiente della variabile predittiva “ore di studio” è 1,7919. Questo ci dice che ogni ora aggiuntiva studiata è associata a un aumento medio di 1,7919 nel punteggio dell’esame.

L’errore standard è 1.0675 , che è una misura della variabilità attorno a questa stima per la pendenza della regressione.

Possiamo utilizzare questo valore per calcolare la statistica t per la variabile predittiva “ore studiate”:

• statistica t = stima del coefficiente/errore standard
• statistica t = 1,7919 / 1,0675
• statistica t = 1.678

Il valore p che corrisponde a questa statistica del test è 0,107. Poiché questo p-value non è inferiore a 0,05, ciò indica che le “ore studiate” non hanno una relazione statisticamente significativa con il voto dell’esame finale.

Poiché l’errore standard della pendenza di regressione era elevato rispetto alla stima del coefficiente della pendenza di regressione, la variabile predittrice non era statisticamente significativa.

Risorse addizionali

Introduzione alla regressione lineare semplice
Introduzione alla regressione lineare multipla
Come leggere e interpretare una tabella di regressione