Come calcolare l'errore standard della media in excel

L’ errore standard della media è un modo per misurare la distribuzione dei valori in un set di dati. Viene calcolato come segue:

Errore standard = s / √n

Oro:

• s : deviazione standard campionaria
• n : dimensione del campione

Puoi calcolare l’errore standard della media di qualsiasi set di dati in Excel utilizzando la seguente formula:

= DEV.ST (intervallo di valori) / SQRT ( COUNT (intervallo di valori))

L’esempio seguente mostra come utilizzare questa formula.

Esempio: errore standard in Excel

Supponiamo di avere il seguente set di dati:

La schermata seguente mostra come calcolare l’errore standard della media per questo set di dati:

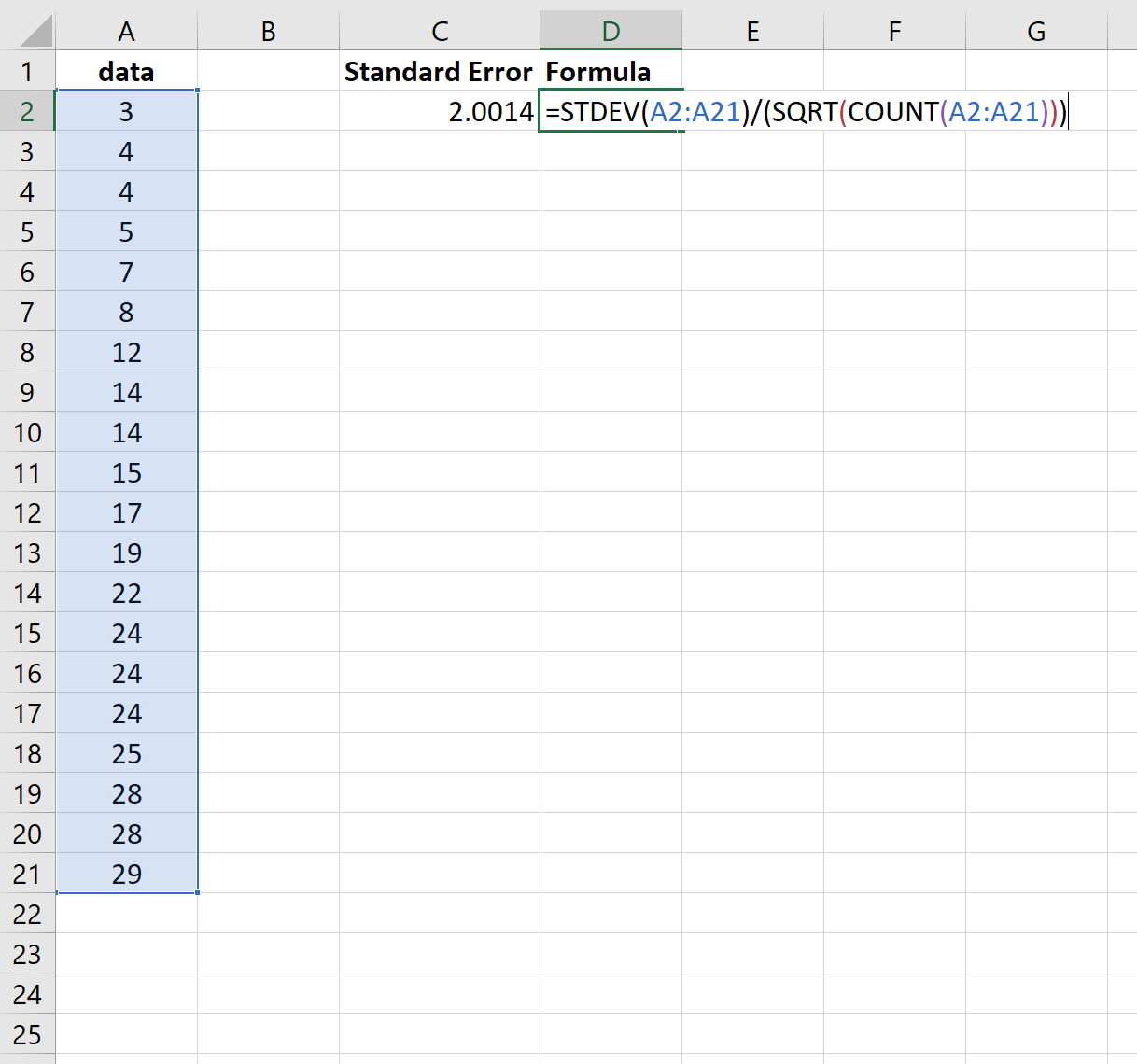
L’errore standard risulta essere 2.0014 .

Tieni presente che la funzione =STDEV() calcola la media campionaria, che è equivalente alla funzione =STDEV.S() in Excel.

Quindi, avremmo potuto utilizzare la seguente formula per ottenere gli stessi risultati:

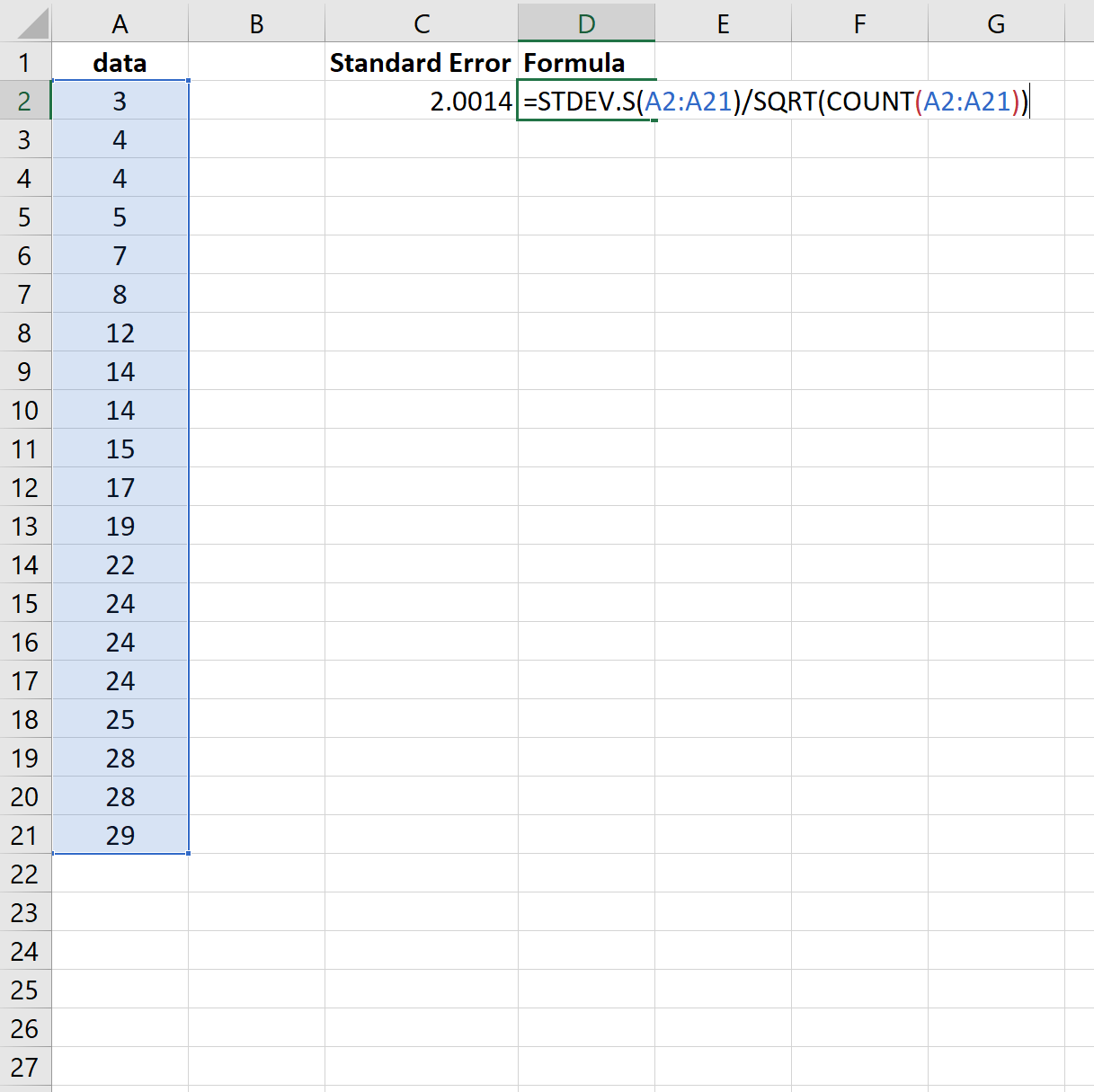
Ancora una volta, l’errore standard risulta essere 2.0014 .

Come interpretare l’errore standard della media

L’errore standard della media è semplicemente una misura della diffusione dei valori attorno alla media. Ci sono due cose da tenere a mente quando si interpreta l’errore standard della media:

1. Quanto maggiore è l’errore standard della media, tanto più sparsi sono i valori attorno alla media in un set di dati.

Per illustrare ciò, considera se modifichiamo l’ultimo valore del set di dati precedente con un numero molto maggiore:

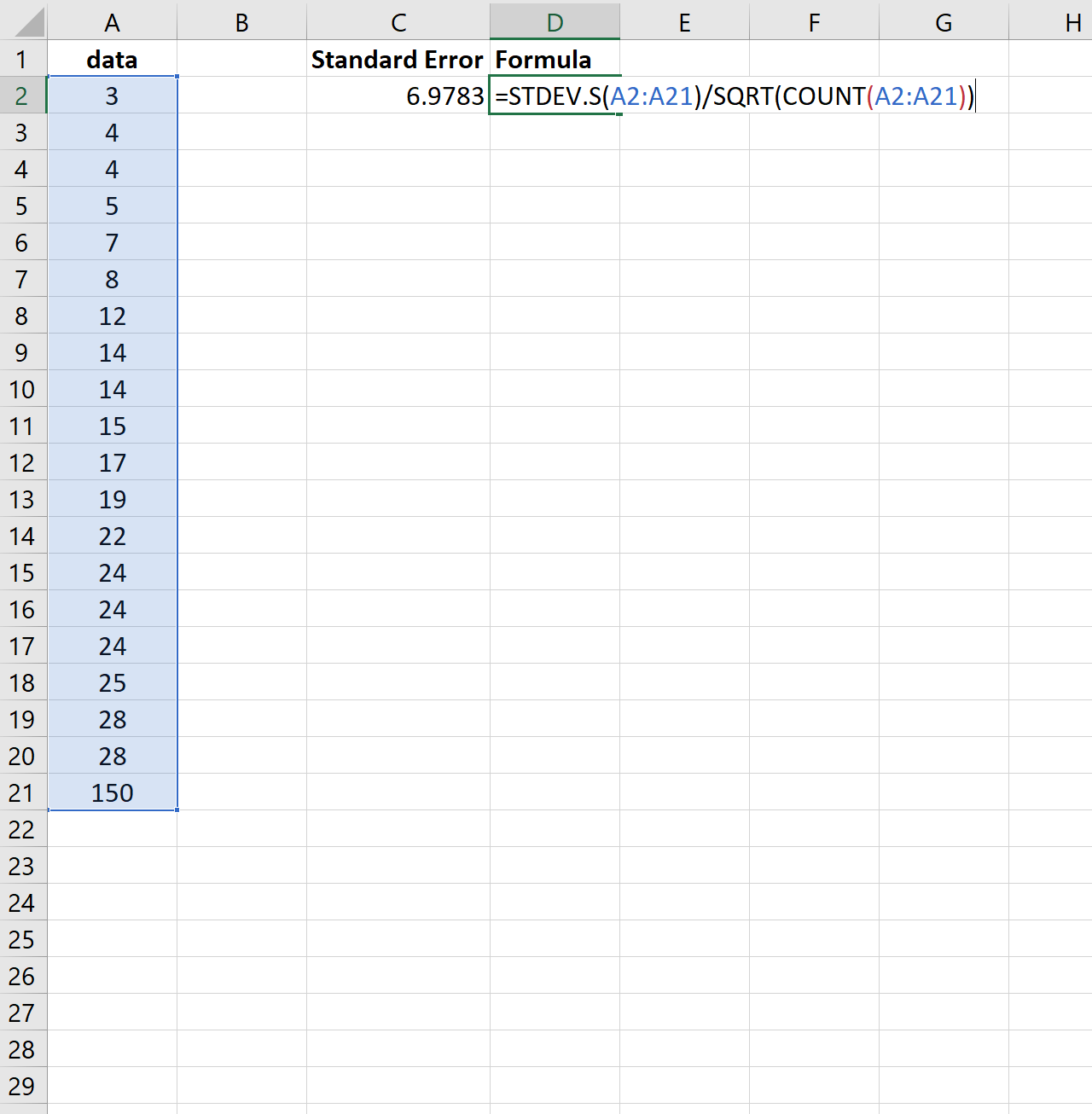
Nota come l’errore standard aumenta da 2.0014 a 6.9783 . Ciò indica che i valori in questo set di dati sono più distribuiti attorno alla media rispetto al set di dati precedente.

2. All’aumentare della dimensione del campione, l’errore standard della media tende a diminuire.

Per illustrare ciò, si consideri l’errore standard della media per i seguenti due insiemi di dati:

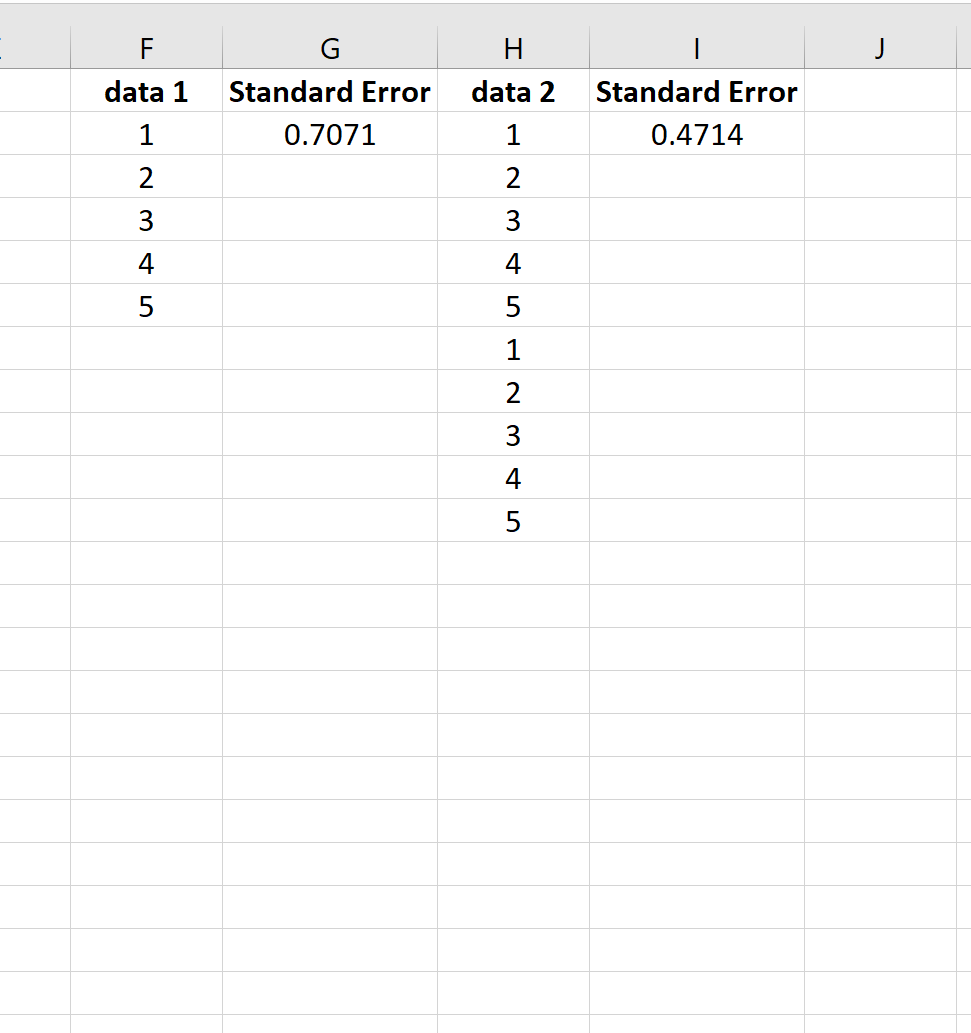
Il secondo set di dati è semplicemente il primo set di dati ripetuto due volte. Quindi entrambi i set di dati hanno la stessa media, ma il secondo set di dati ha una dimensione campionaria maggiore e quindi ha un errore standard più piccolo.