Come calcolare l'errore standard di regressione in excel

Adattiamo un modello di regressione lineare , il modello assume la seguente forma:

Y = β ₀ + β ₁ X + … + β _i

dove ϵ è un termine di errore indipendente da X.

Non importa come X possa essere utilizzato per prevedere i valori di Y, nel modello ci sarà sempre un errore casuale.

Un modo per misurare la dispersione di questo errore casuale è utilizzare l’ errore standard del modello di regressione , che è un modo per misurare la deviazione standard dei residui ϵ.

Questo tutorial fornisce un esempio passo passo di come calcolare l’errore standard di un modello di regressione in Excel.

Passaggio 1: creare i dati

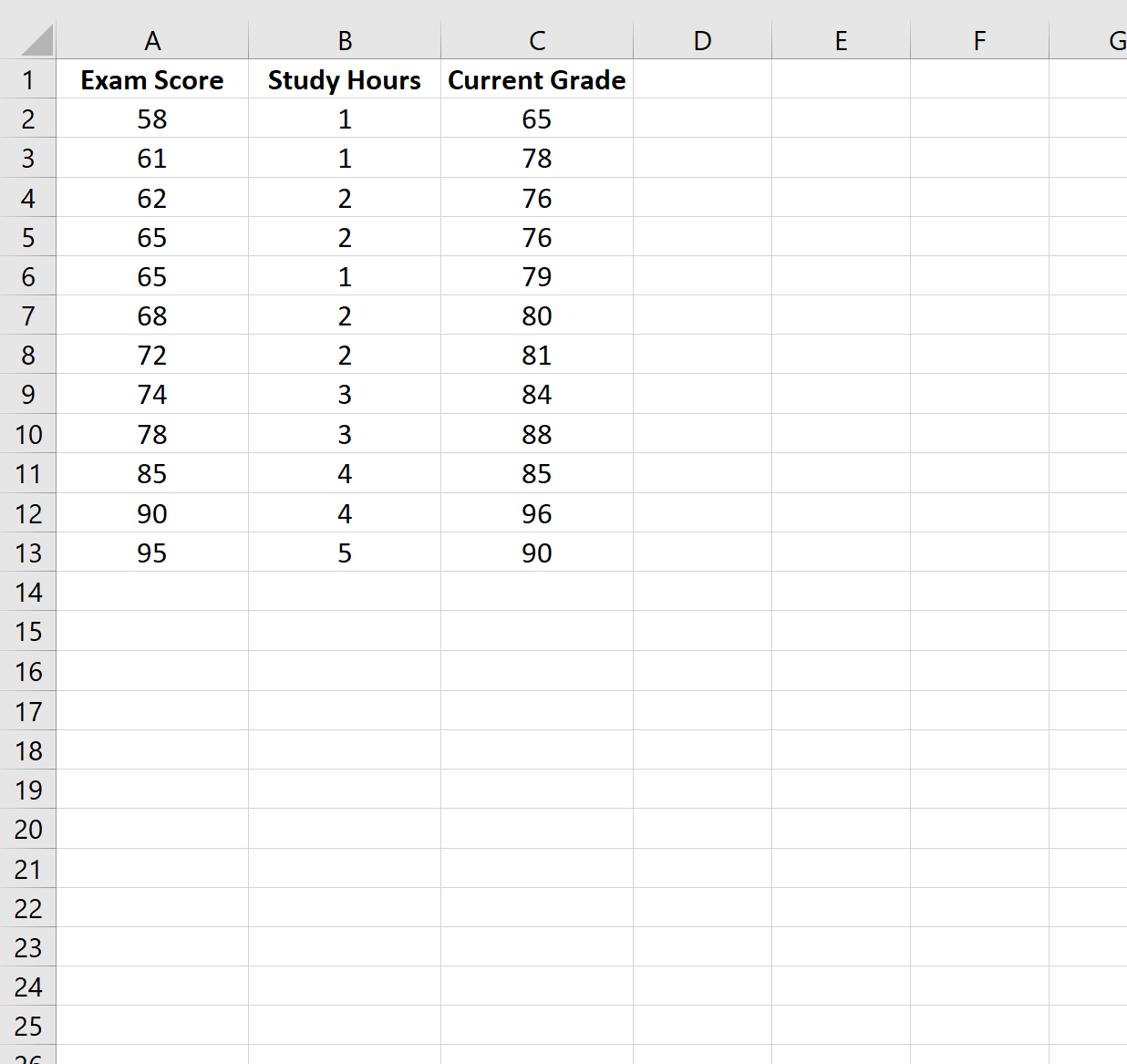
Per questo esempio, creeremo un set di dati contenente le seguenti variabili per 12 studenti diversi:

• Risultato dell’esame
• Ore passate a studiare
• Classe attuale

Passaggio 2: adattare il modello di regressione

Successivamente, adatteremo un modello di regressione lineare multipla utilizzando il punteggio dell’esame come variabile di risposta e le ore di studio e il voto attuale come variabili predittive.

Per fare ciò, fai clic sulla scheda Dati lungo la barra multifunzione superiore, quindi fai clic su Analisi dati :

Se questa opzione non è disponibile, è necessario prima caricare il Data Analysis ToolPak .

Nella finestra che appare, seleziona Regressione . Nella nuova finestra che appare, fornisci le seguenti informazioni:

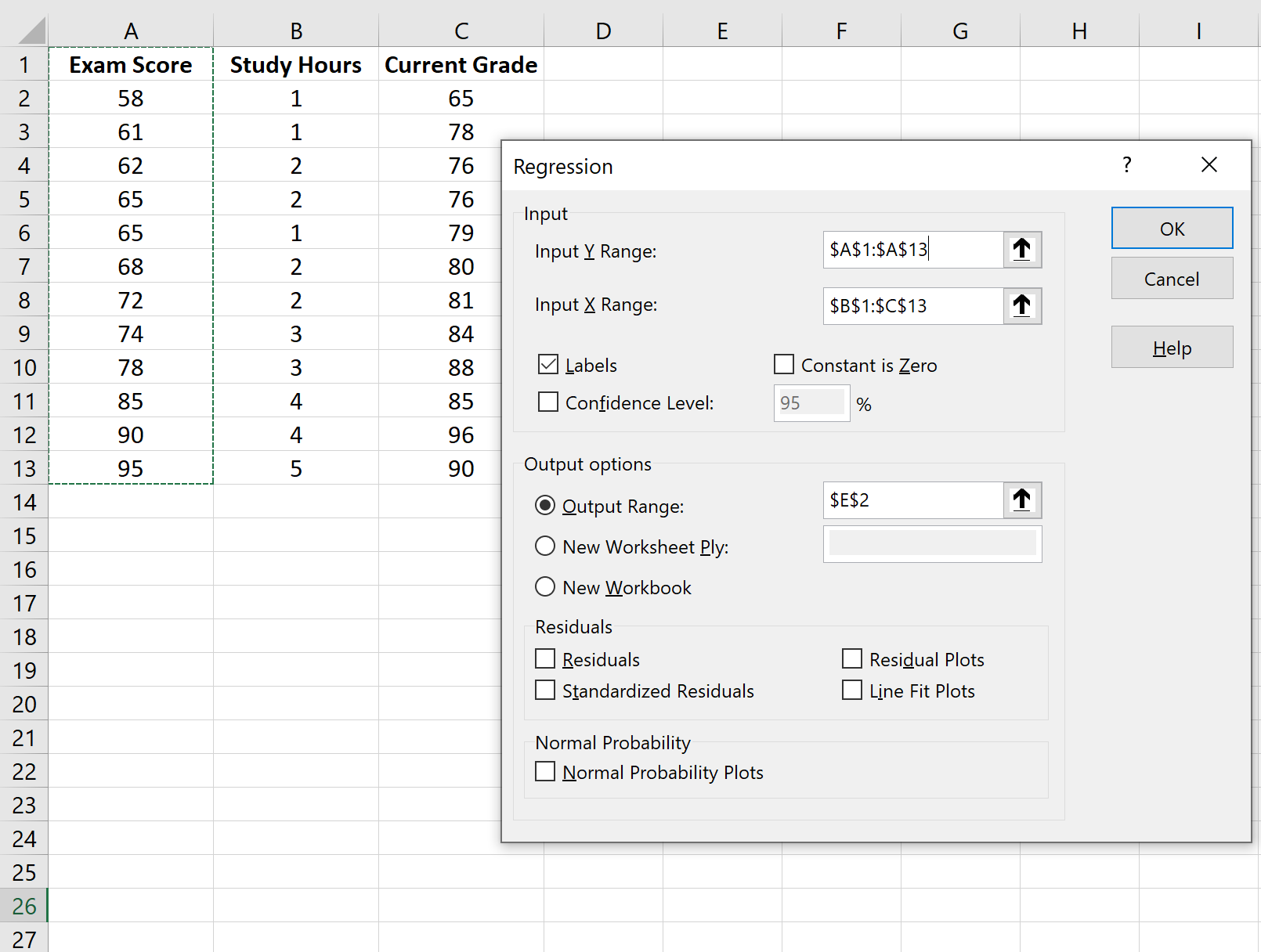
Dopo aver fatto clic su OK , verrà visualizzato l’output del modello di regressione:

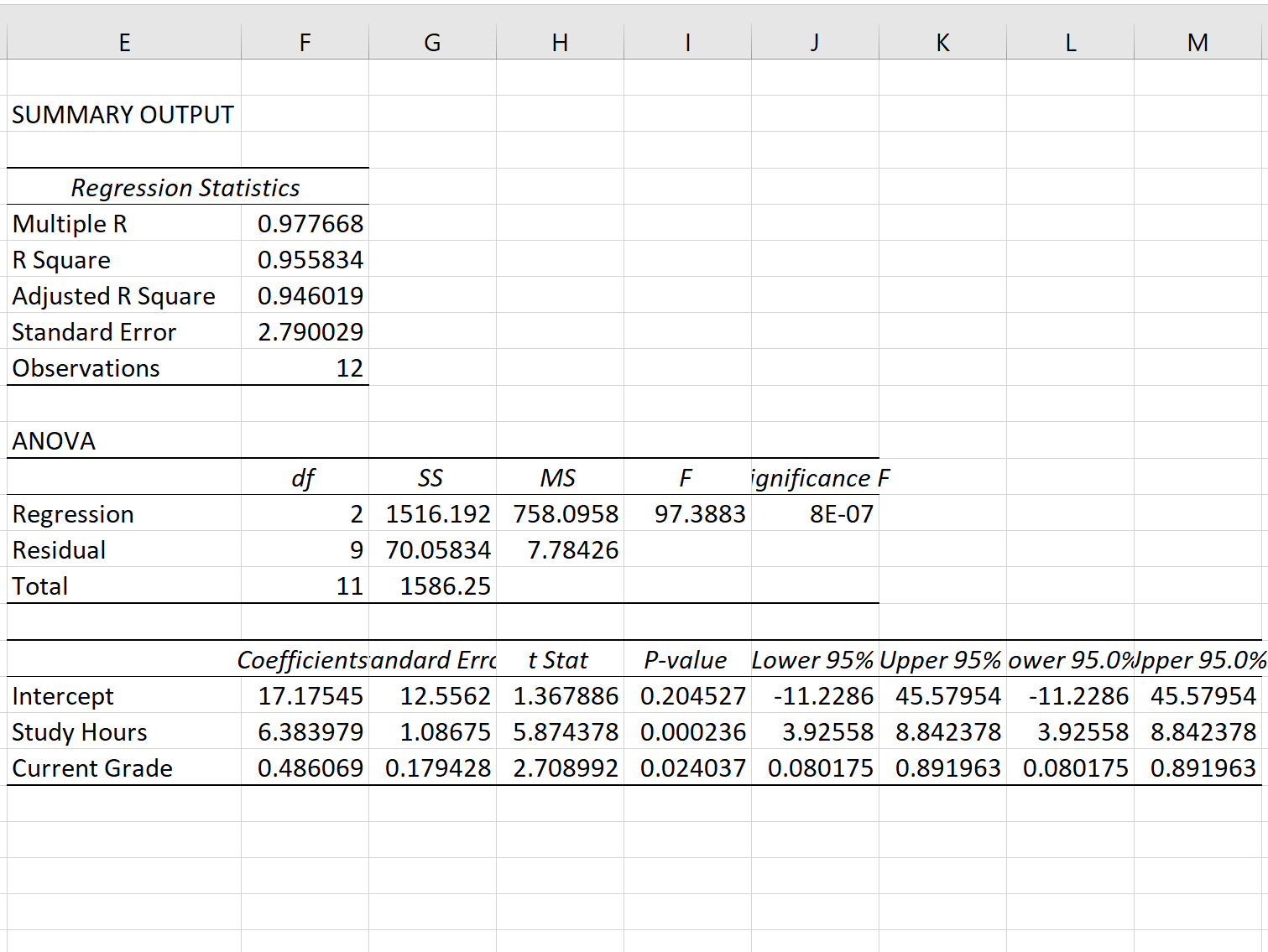
Passaggio 3: interpretare l’errore standard di regressione

L’errore standard del modello di regressione è il numero accanto all’errore standard :

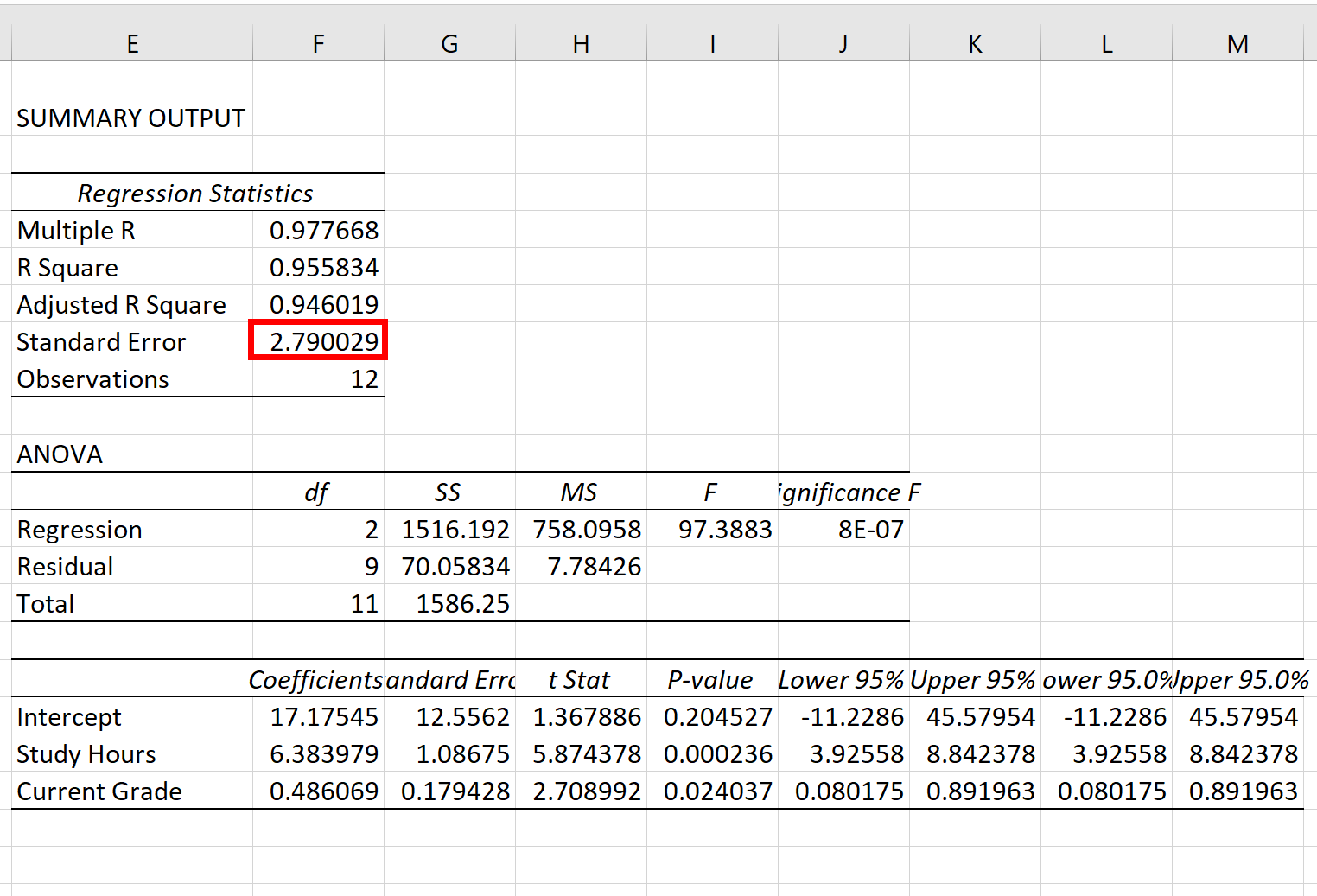
L’errore standard di questo particolare modello di regressione risulta essere 2.790029 .

Questo numero rappresenta la distanza media tra i risultati effettivi dell’esame e i risultati dell’esame previsti dal modello.

Tieni presente che alcuni risultati dell’esame saranno distanti più di 2,79 unità dal punteggio previsto, mentre altri saranno più vicini. Ma, in media, la distanza tra i risultati effettivi dell’esame e i risultati previsti è 2,790029 .

Si noti inoltre che un errore standard di regressione più piccolo indica che un modello di regressione si adatta più fedelmente a un set di dati.

Pertanto, se adattiamo un nuovo modello di regressione al set di dati e otteniamo un errore standard, diciamo, di 4,53 , questo nuovo modello sarebbe meno efficace nel prevedere i punteggi degli esami rispetto al modello precedente.

Risorse addizionali

Un altro modo comune per misurare l’accuratezza di un modello di regressione è utilizzare R-quadrato. Dai un’occhiata aquesto articolo per un’interessante spiegazione dei vantaggi derivanti dall’utilizzo dell’errore standard di regressione per misurare l’accuratezza rispetto all’R quadrato.