Qual è l'errore standard della stima? (definizione & #038; esempio)

L’ errore standard della stima è un modo per misurare l’accuratezza delle previsioni effettuate da un modello di regressione.

Spesso notato σ _est , viene calcolato come segue:

σ _è = √ Σ(y – ŷ) ² /n

Oro:

• y: il valore osservato
• ŷ: il valore previsto
• n: il numero totale di osservazioni

L’errore standard della stima ci dà un’idea di quanto bene un modello di regressione si adatta a un set di dati. Particolarmente:

• Minore è il valore, migliore è l’adattamento.
• Maggiore è il valore, peggiore è l’adattamento.

Per un modello di regressione con un errore standard piccolo della stima, i punti dati saranno strettamente raggruppati attorno alla linea di regressione stimata:

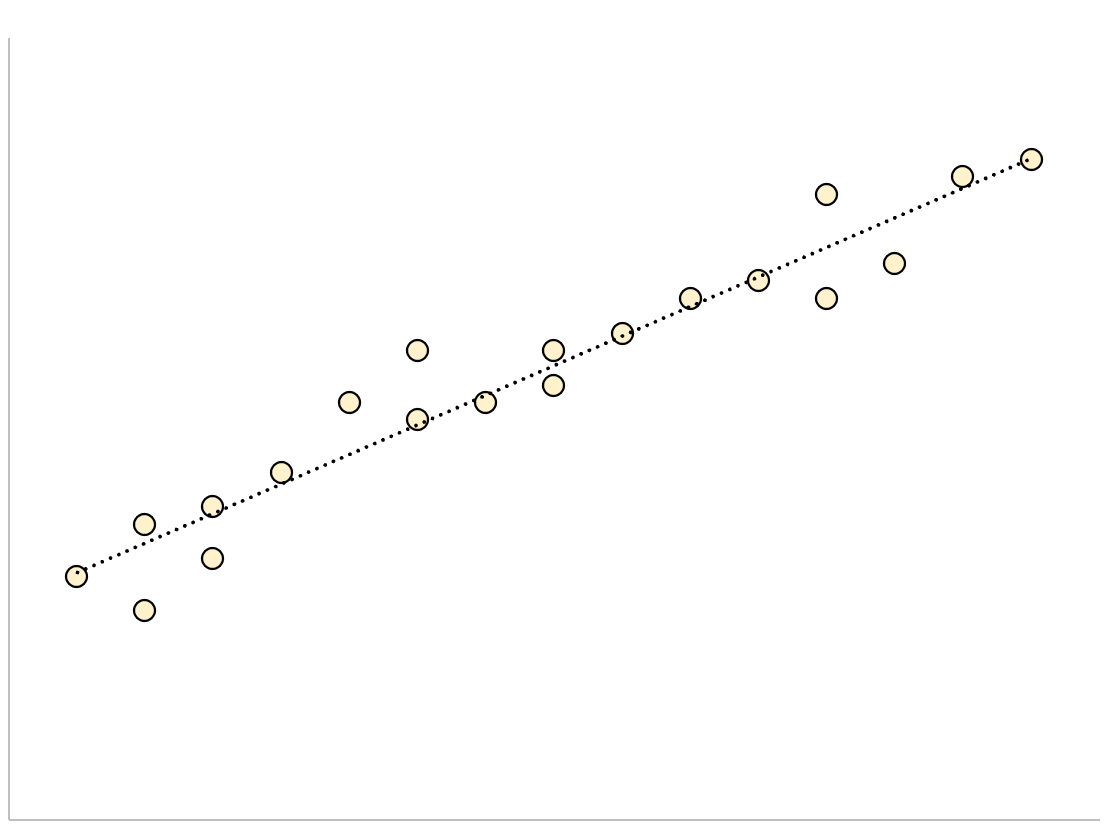
Al contrario, per un modello di regressione con un errore standard di stima ampio, i punti dati saranno sparsi in modo più approssimativo lungo la linea di regressione:

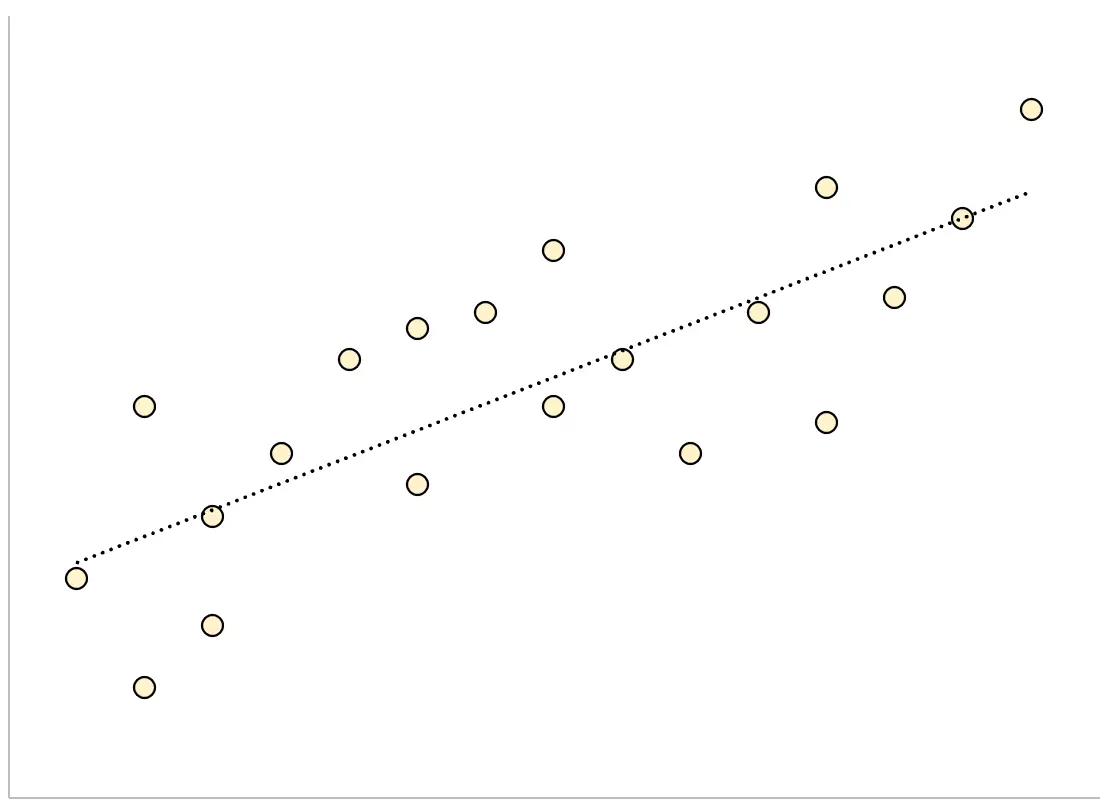
L’esempio seguente mostra come calcolare e interpretare l’errore standard della stima per un modello di regressione in Excel.

Esempio: errore standard di stima in Excel

Utilizzare i passaggi seguenti per calcolare l’errore standard della stima per un modello di regressione in Excel.

Passaggio 1: inserisci i dati

Innanzitutto, inserisci i valori del set di dati:

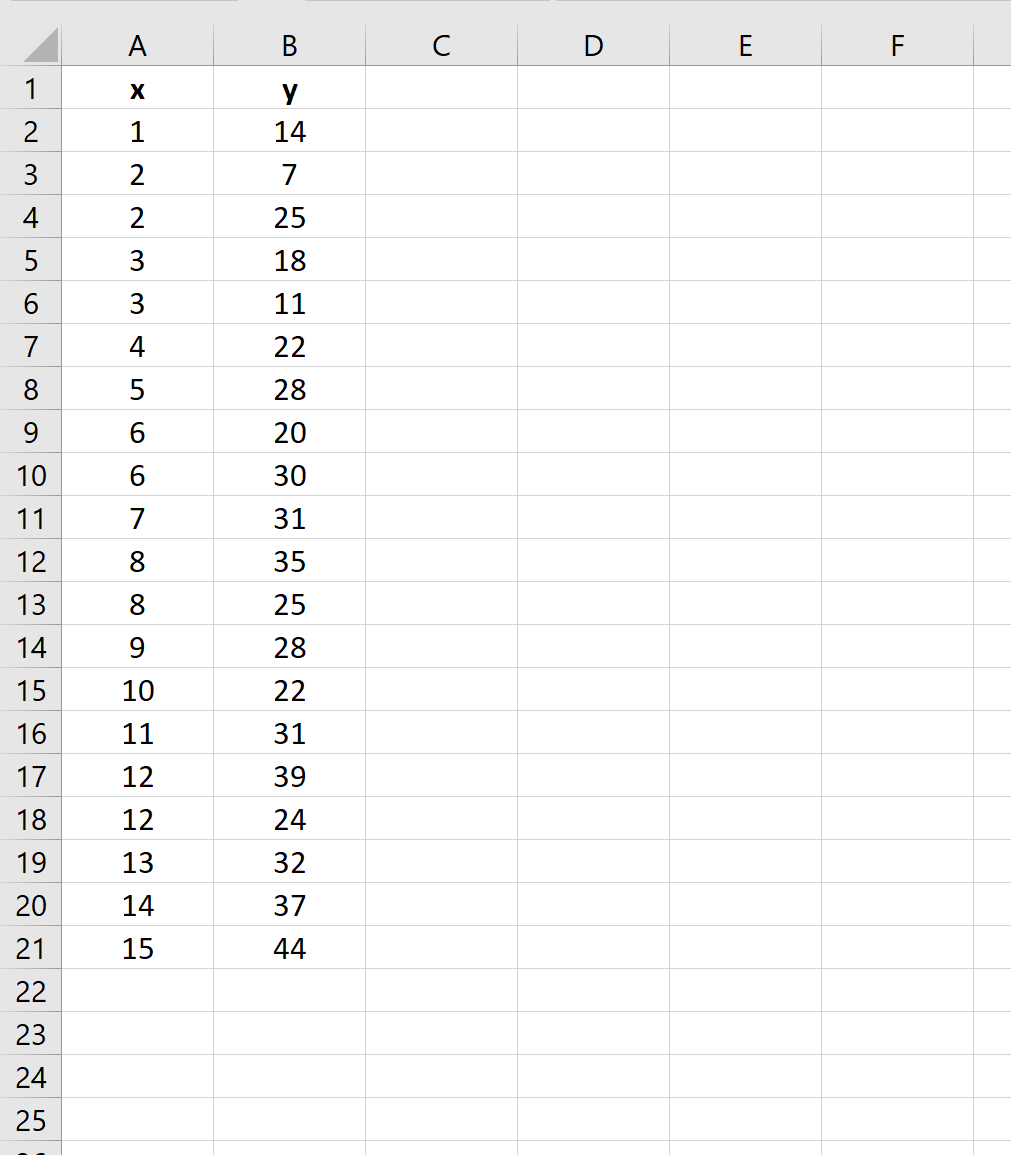
Passaggio 2: eseguire la regressione lineare

Successivamente, fai clic sulla scheda Dati lungo la barra multifunzione superiore. Quindi fare clic sull’opzione Analisi dati nel gruppo Analizza .

Se non vedi questa opzione, devi prima caricare Analysis ToolPak .

Nella nuova finestra visualizzata, fare clic su Regressione , quindi su OK .

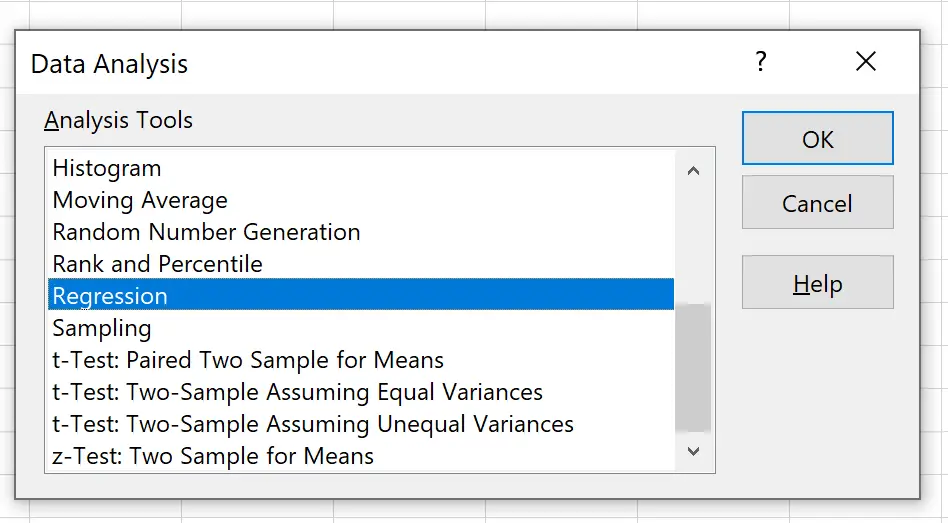
Nella nuova finestra che appare, fornisci le seguenti informazioni:

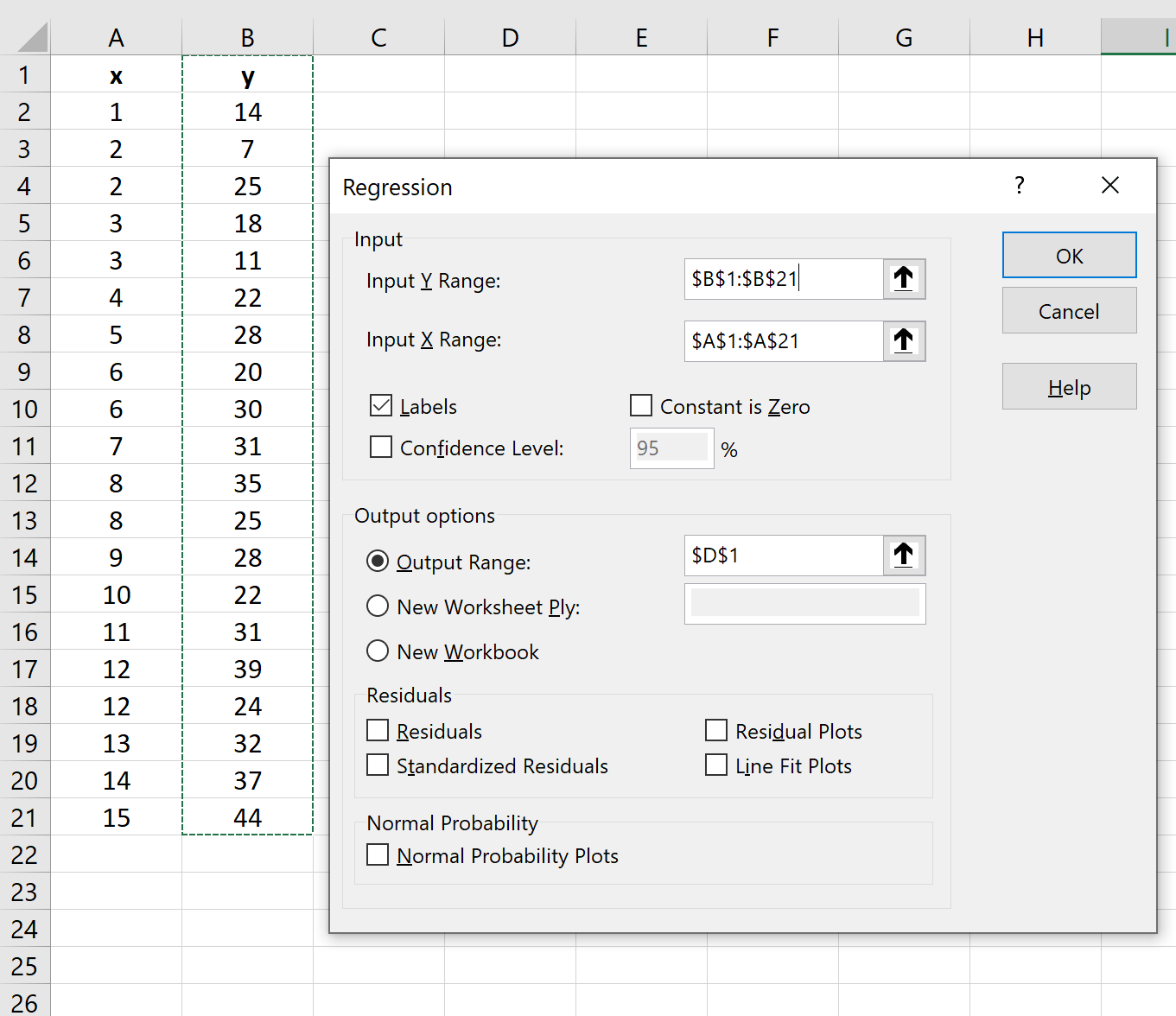
Dopo aver fatto clic su OK , verrà visualizzato il risultato della regressione:

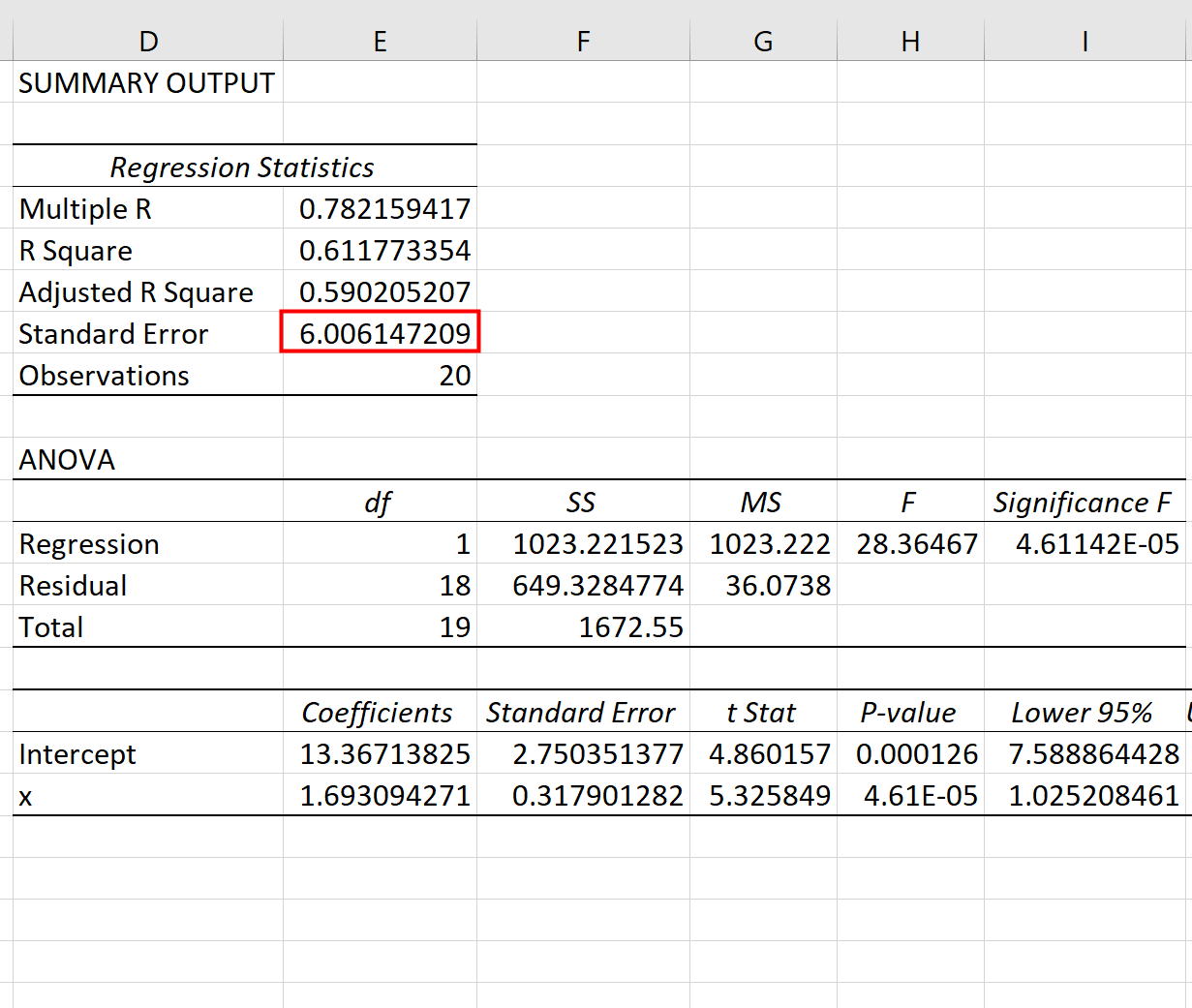
Possiamo utilizzare i coefficienti della tabella di regressione per costruire l’equazione di regressione stimata:

ŷ = 13.367 + 1.693(x)

E possiamo vedere che l’errore standard della stima per questo modello di regressione risulta essere 6.006 . In termini semplici, questo ci dice che il punto dati medio è a 6.006 unità dalla linea di regressione.

Possiamo utilizzare l’equazione di regressione stimata e l’errore standard della stima per costruire un intervallo di confidenza al 95% per il valore previsto di un determinato punto dati.

Ad esempio, supponiamo che x sia uguale a 10. Utilizzando l’equazione di regressione stimata, prevediamo che y sarebbe uguale a:

ŷ = 13.367 + 1.693*(10) = 30.297

E possiamo ottenere l’intervallo di confidenza del 95% per questa stima utilizzando la seguente formula:

• CI al 95% = [ŷ – 1,96*σ _è , ŷ + 1,96*σ _è ]

Per il nostro esempio, l’intervallo di confidenza al 95% verrebbe calcolato come:

• CI al 95% = [ŷ – 1,96*σ _è , ŷ + 1,96*σ _è ]
• IC al 95% = [30,297 – 1,96*6,006, 30,297 + 1,96*6,006]
• IC al 95% = [18.525, 42.069]

Risorse addizionali

Come eseguire una regressione lineare semplice in Excel
Come eseguire la regressione lineare multipla in Excel
Come creare un grafico residuo in Excel