4 esempi di utilizzo dei test chi-quadrato nella vita reale
In statistica, esistono due diversi tipi di test Chi-quadrato:
1. Test della bontà di adattamento del chi quadrato : utilizzato per determinare se una variabile categoriale segue o meno una distribuzione ipotetica.
2. Il test di indipendenza del Chi quadrato – Utilizzato per determinare se esiste o meno un’associazione significativa tra due variabili categoriali.
In questo articolo condividiamo diversi esempi di come ciascuno di questi tipi di test Chi-quadrato viene utilizzato in situazioni reali.
Esempio 1: test della bontà di adattamento del chi quadrato
Supponiamo che il proprietario di un negozio affermi che un numero uguale di clienti si reca nel suo negozio ogni giorno della settimana.
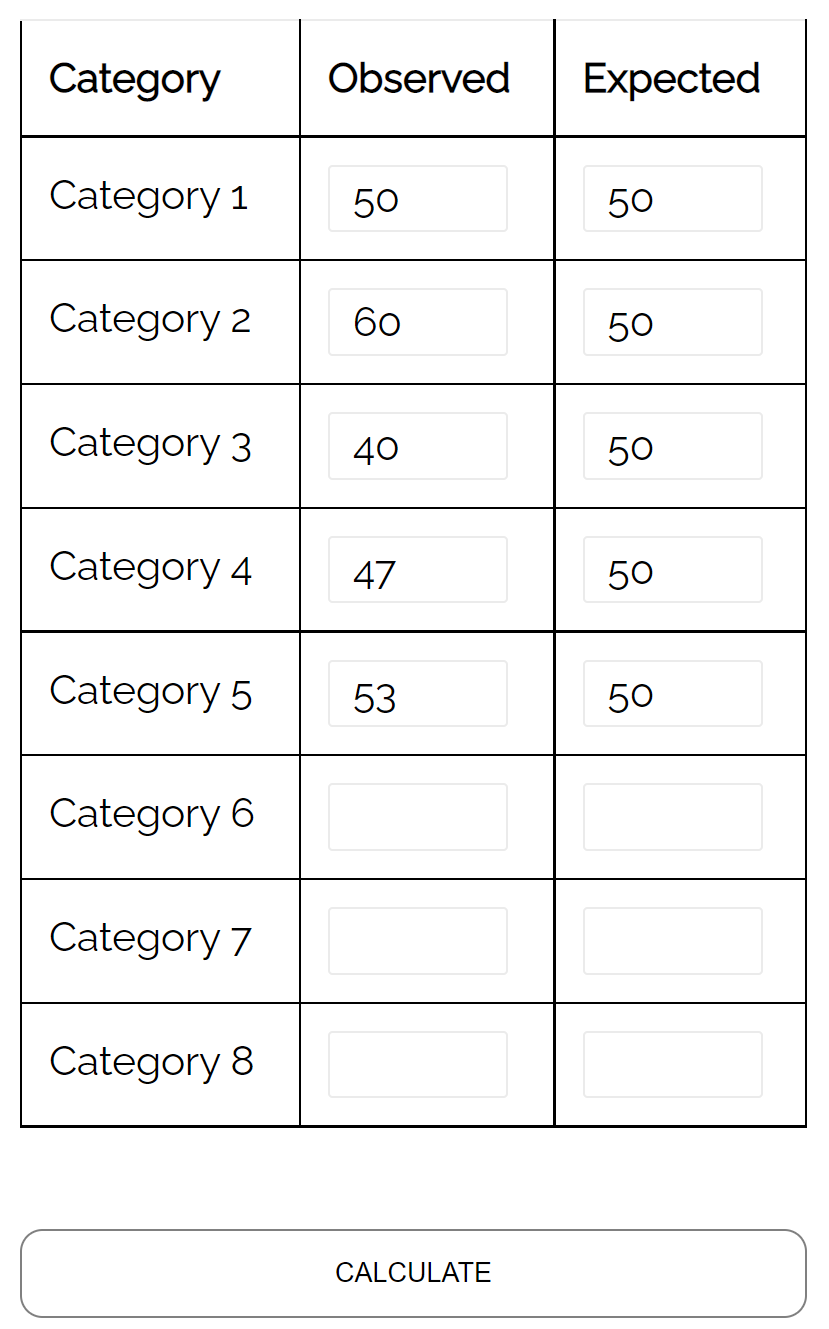
Per verificare questa ipotesi, registra il numero di clienti che entrano nel negozio in una determinata settimana e trova quanto segue:
- Lunedì: 50 clienti
- Martedì: 60 clienti
- Mercoledì: 40 clienti
- Giovedì: 47 clienti
- Venerdì: 53 clienti
Può utilizzare un test di bontà di adattamento del chi quadrato per determinare se la distribuzione dei clienti che arrivano ogni giorno è coerente con la sua ipotesi di distribuzione.
Utilizzando il calcolatore del test della bontà di adattamento del chi quadrato , può vedere che il valore p del test è 0,359 .

Poiché questo valore p non è inferiore a 0,05, non ci sono prove sufficienti per affermare che la reale distribuzione dei clienti sia diversa da quella affermata dal proprietario del negozio.
Esempio 2: test della bontà di adattamento del chi quadrato
Supponiamo che un biologo affermi che un numero uguale di quattro specie diverse di cervi entri ogni settimana in una determinata area boschiva di una foresta.
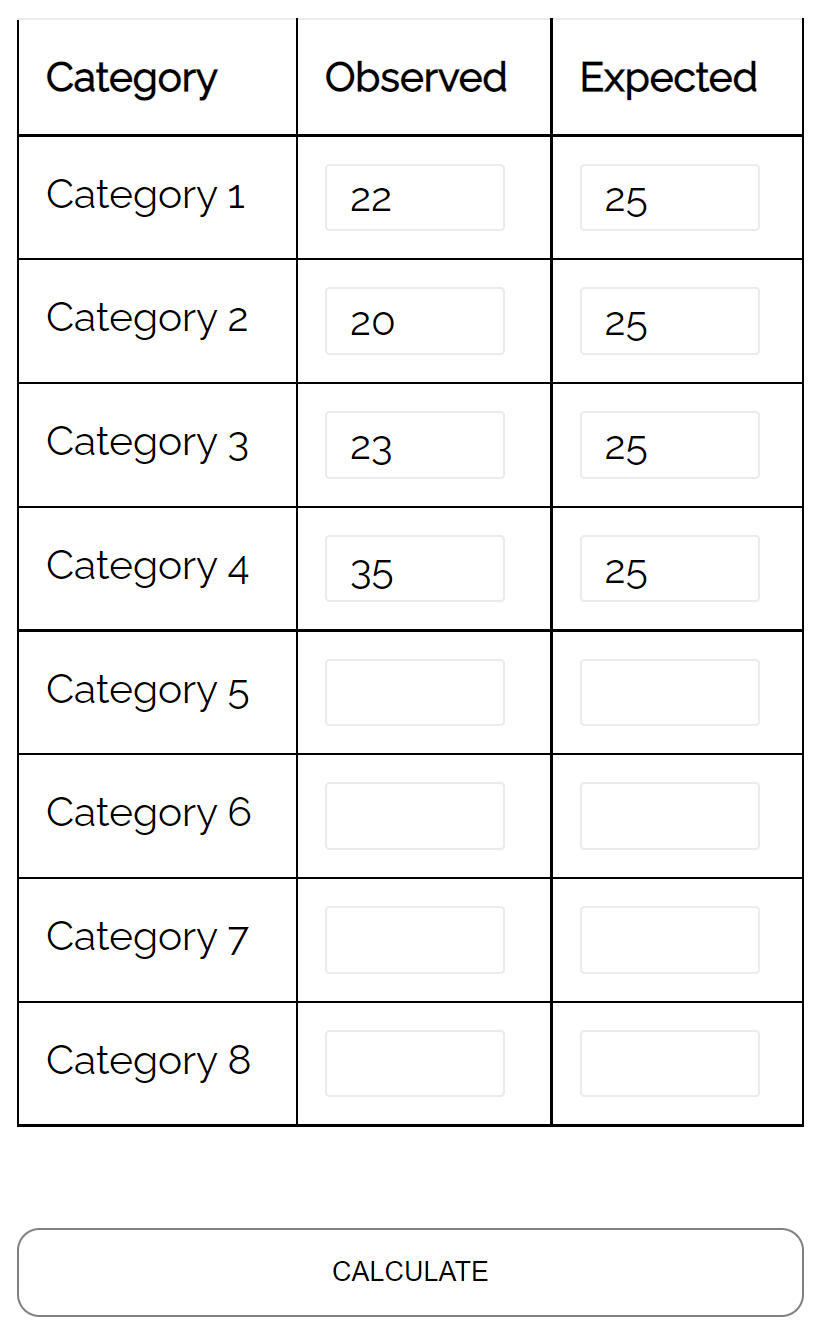
Per verificare questa ipotesi, registra il numero di ciascuna specie di cervi che entra nell’area boschiva nel corso di una settimana:
- Specie n. 1: 22
- Specie n. 2: 20
- Specie n. 3: 23
- Specie n. 4: 35
Può utilizzare un test di bontà di adattamento chi quadrato per determinare se la distribuzione delle specie di cervi che entrano nell’area boschiva della foresta ogni settimana è coerente con la sua distribuzione ipotetica.
Utilizzando il calcolatore del test della bontà di adattamento del chi quadrato , può vedere che il valore p per il test è 0,137 .
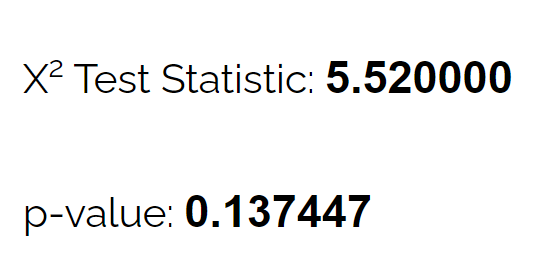
Poiché questo valore p non è inferiore a 0,05, non ci sono prove sufficienti per affermare che la vera distribuzione dei cervi sia diversa da quella affermata dal biologo.
Esempio 3: test di indipendenza del chi-quadrato
Supponiamo che un decisore politico di una certa città voglia sapere se il genere è associato o meno alle preferenze di un partito politico.
Decide di prendere un semplice campione casuale di 500 elettori e chiedere loro quale sia la loro preferenza per il partito politico. La tabella seguente presenta i risultati dell’indagine:
| Repubblicano | Democratico | Indipendente | Totale | |
| Maschio | 120 | 90 | 40 | 250 |
| Femmina | 110 | 95 | 45 | 250 |
| Totale | 230 | 185 | 85 | 500 |
Può utilizzare un test di indipendenza chi quadrato per determinare se esiste un’associazione statisticamente significativa tra le due variabili.
Utilizzando il calcolatore del test di indipendenza del chi quadrato , può vedere che il valore p del test è 0,649 .
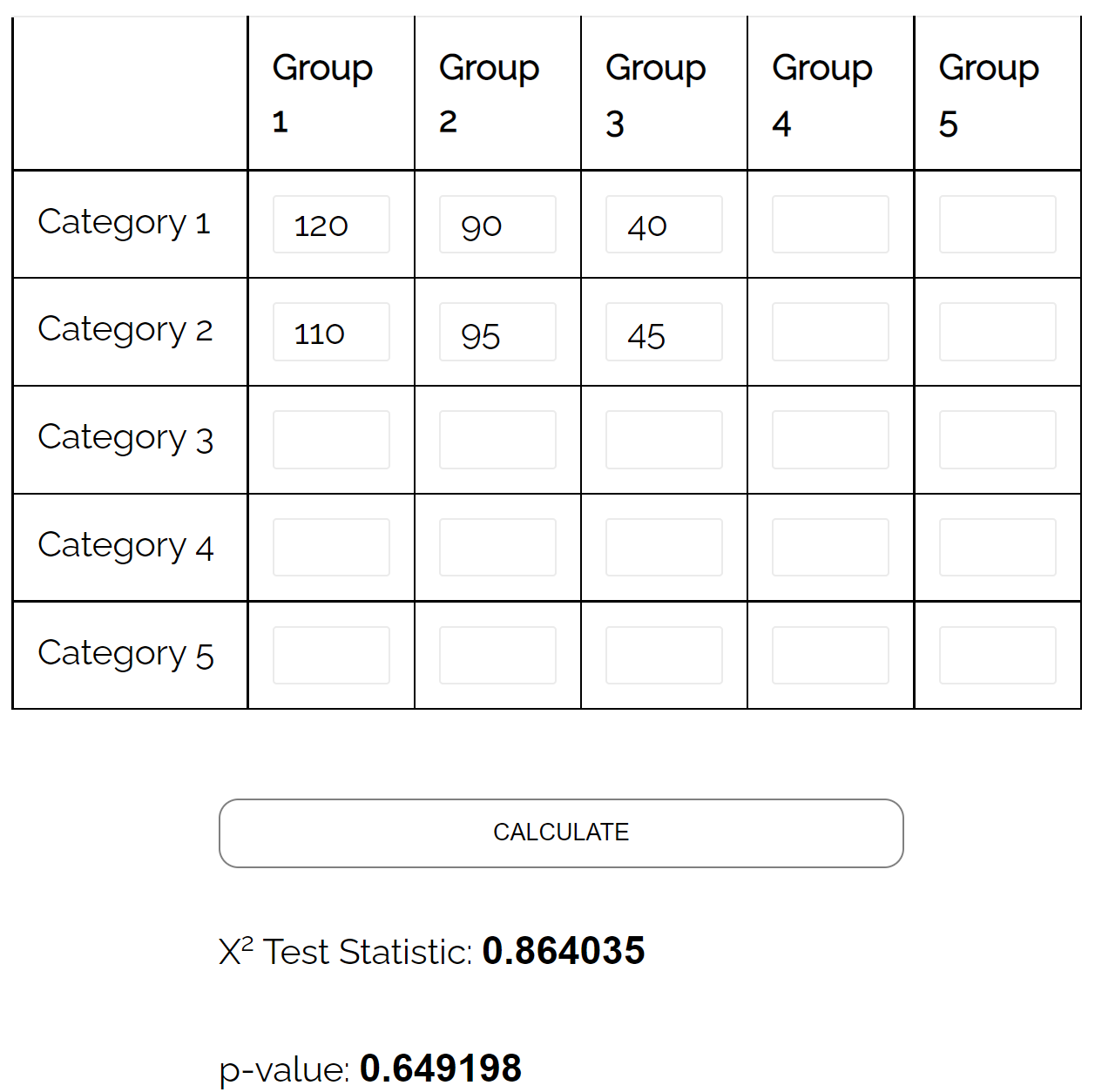
Poiché il valore p non è inferiore a 0,05, non ci sono prove sufficienti per affermare che esista un’associazione tra genere e preferenza del partito politico.
Esempio 4: test di indipendenza del chi-quadrato
Supponiamo che un ricercatore voglia sapere se lo stato civile è associato o meno al livello di istruzione.
Decide di prendere un campione casuale semplice di 300 individui e ottiene i seguenti risultati:
| Scuola superiore | Scapoli | Maestro o superiore | Totale | |
| Sposato | 20 | 100 | 35 | 155 |
| Laurea breve | 50 | 80 | 15 | 145 |
| Totale | 70 | 180 | 50 | 300 |
Può utilizzare un test di indipendenza chi quadrato per determinare se esiste un’associazione statisticamente significativa tra le due variabili.
Utilizzando il calcolatore del test di indipendenza del chi quadrato , può vedere che il valore p del test è 0,000011 .
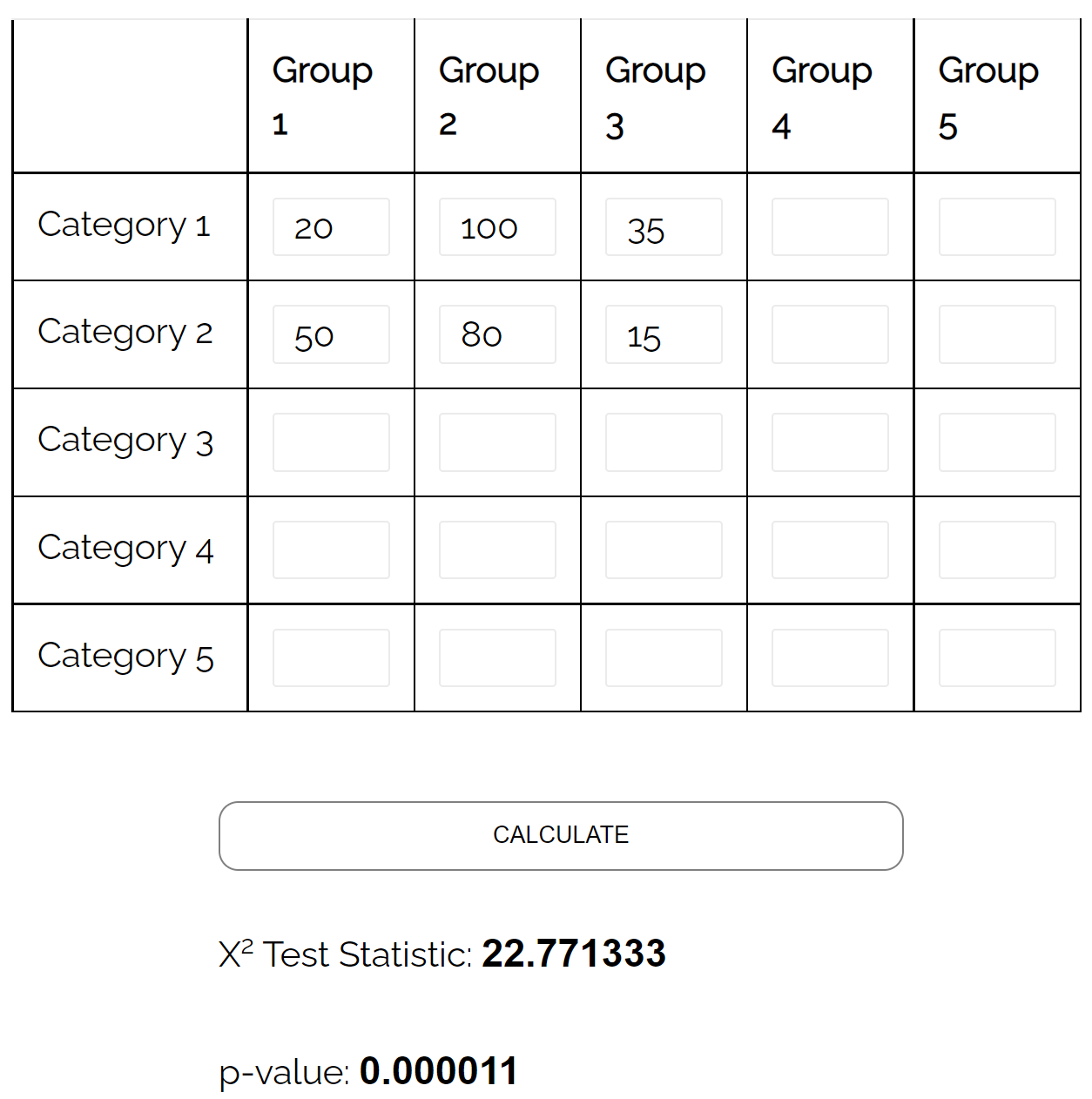
Poiché il valore p è inferiore a 0,05, ci sono prove sufficienti per affermare che esiste un’associazione tra stato civile e livello di istruzione.
Risorse addizionali
I seguenti tutorial forniscono un’introduzione ai diversi tipi di test Chi-quadrato:
I seguenti tutorial spiegano la differenza tra i test Chi-quadrato e altri test statistici: