Come creare foreste casuali in r (passo dopo passo)

Quando la relazione tra un insieme di variabili predittive e una variabile di risposta è molto complessa, spesso utilizziamo metodi non lineari per modellare la relazione tra loro.

Uno di questi metodi è costruire un albero decisionale . Tuttavia, lo svantaggio di utilizzare un unico albero decisionale è che tende a soffrire di un’elevata varianza .

Cioè, se dividiamo il set di dati in due metà e applichiamo l’albero decisionale a entrambe le metà, i risultati potrebbero essere molto diversi.

Un metodo che possiamo utilizzare per ridurre la varianza di un singolo albero decisionale è costruire un modello di foresta casuale , che funziona come segue:

1. Prendi b campioni bootstrap dal set di dati originale.

2. Creare un albero decisionale per ciascun campione di bootstrap.

• Quando si costruisce l’albero, ogni volta che viene considerata una suddivisione, solo un campione casuale di m predittori viene considerato candidato alla suddivisione dall’intero set di p predittori. Generalmente scegliamo m uguale a √p .

3. Media delle previsioni di ciascun albero per ottenere un modello finale.

Si scopre che le foreste casuali tendono a produrre modelli molto più accurati rispetto ai singoli alberi decisionali e persino ai modelli impacchettati .

Questo tutorial fornisce un esempio dettagliato di come creare un modello di foresta casuale per un set di dati in R.

Passaggio 1: caricare i pacchetti necessari

Per prima cosa caricheremo i pacchetti necessari per questo esempio. Per questo semplice esempio, abbiamo bisogno di un solo pacchetto:

 library (randomForest)

Passaggio 2: modificare il modello della foresta casuale

Per questo esempio, utilizzeremo un set di dati R integrato chiamato Air Quality che contiene misurazioni della qualità dell’aria nella città di New York nell’arco di 153 giorni individuali.

 #view structure of air quality dataset
str(airquality)

'data.frame': 153 obs. of 6 variables:
 $ Ozone: int 41 36 12 18 NA 28 23 19 8 NA ...
 $Solar.R: int 190 118 149 313 NA NA 299 99 19 194 ...
 $ Wind: num 7.4 8 12.6 11.5 14.3 14.9 8.6 13.8 20.1 8.6 ...
 $ Temp: int 67 72 74 62 56 66 65 59 61 69 ...
 $Month: int 5 5 5 5 5 5 5 5 5 5 ...
 $Day: int 1 2 3 4 5 6 7 8 9 10 ...

#find number of rows with missing values
sum(! complete . cases (airquality))

[1] 42

Questo set di dati ha 42 righe con valori mancanti. Pertanto, prima di adattare un modello di foresta casuale, inseriremo i valori mancanti in ciascuna colonna con le mediane delle colonne:

 #replace NAs with column medians
for (i in 1: ncol (air quality)) {
  airquality[,i][ is . na (airquality[, i])] <- median (airquality[, i], na . rm = TRUE )
}

Correlato: Come imputare i valori mancanti in R

Il codice seguente mostra come adattare un modello di foresta casuale in R utilizzando la funzione randomForest() del pacchetto randomForest .

 #make this example reproducible
set.seed(1)

#fit the random forest model
model <- randomForest(
  formula = Ozone ~ .,
  data = airquality
)

#display fitted model
model

Call:
 randomForest(formula = Ozone ~ ., data = airquality) 
               Type of random forest: regression
                     Number of trees: 500
No. of variables tried at each split: 1

          Mean of squared residuals: 327.0914
                    % Var explained: 61

#find number of trees that produce lowest test MSE
which.min(model$mse)

[1] 82

#find RMSE of best model
sqrt(model$mse[ which . min (model$mse)]) 

[1] 17.64392

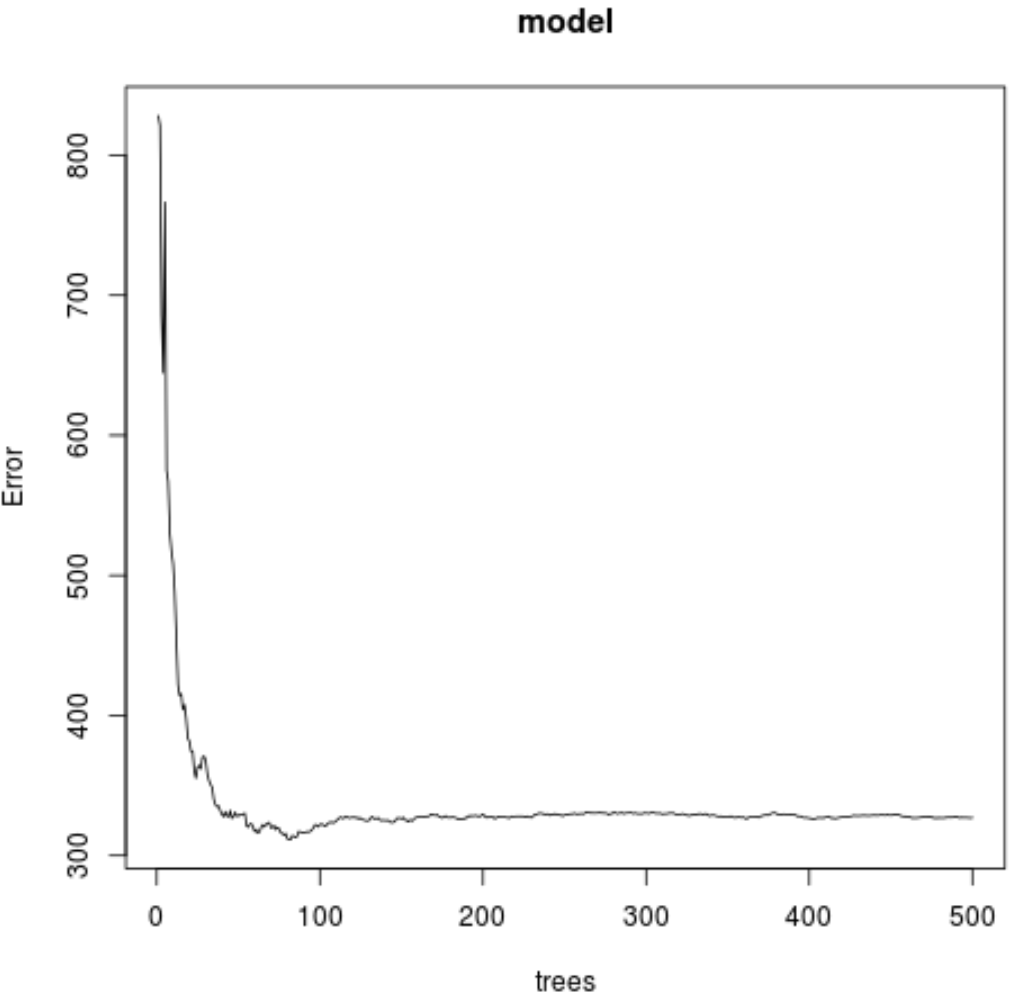
Dal risultato, possiamo vedere che il modello che ha prodotto l’errore quadratico medio (MSE) più basso del test utilizzava 82 alberi.

Possiamo anche vedere che l’errore quadratico medio di questo modello era 17.64392 . Possiamo considerarlo come la differenza media tra il valore previsto per l’ozono e il valore effettivamente osservato.

Possiamo anche utilizzare il seguente codice per produrre un grafico del test MSE in base al numero di alberi utilizzati:

 #plot the MSE test by number of trees
plot(model)

E possiamo utilizzare la funzione varImpPlot() per creare un grafico che mostri l’importanza di ciascuna variabile predittrice nel modello finale:

 #produce variable importance plot
varImpPlot(model) 

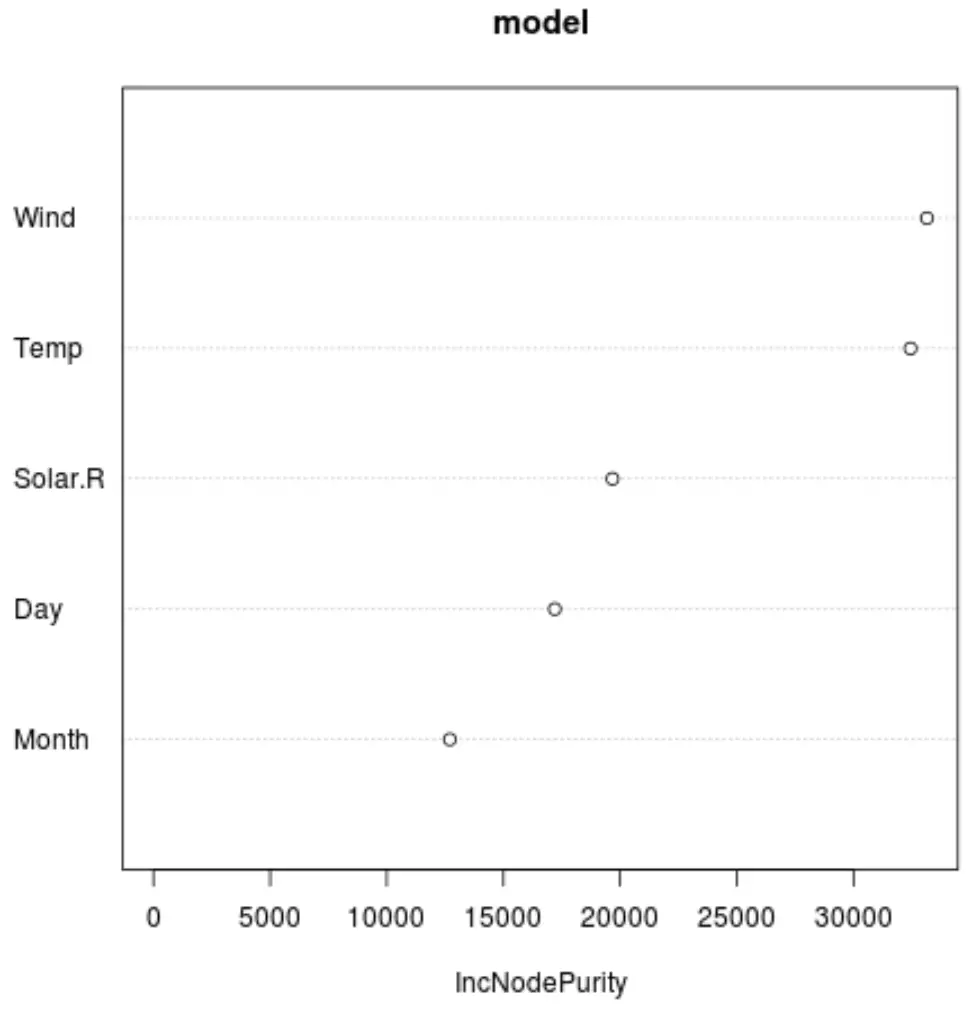
L’asse x mostra l’aumento medio della purezza dei nodi degli alberi di regressione in funzione della suddivisione tra i diversi predittori visualizzati sull’asse y.

Dal grafico, possiamo vedere che il Vento è la variabile predittiva più importante, seguita da vicino da Temp .

Passaggio 3: adattare il modello

Per impostazione predefinita, la funzione randomForest() utilizza 500 alberi e (predittori totali/3) predittori selezionati casualmente come potenziali candidati per ciascuna suddivisione. Possiamo regolare questi parametri usando la funzione tuneRF() .

Il codice seguente mostra come trovare il modello ottimale utilizzando le seguenti specifiche:

• ntreeTry: il numero di alberi da costruire.
• mtryStart: il numero iniziale di variabili predittive da prendere in considerazione ad ogni divisione.
• stepFactor: fattore da aumentare fino a quando l’errore stimato di esaurimento del sacchetto non smette di migliorare di un certo importo.
• miglioramento: la quantità di cui l’errore di uscita del sacco deve essere migliorato per continuare ad aumentare il fattore di passo.

 model_tuned <- tuneRF(
               x=airquality[,-1], #define predictor variables
               y=airquality$Ozone, #define response variable
               ntreeTry= 500 ,
               mtryStart= 4 , 
               stepFactor= 1.5 ,
               improve= 0.01 ,
               trace= FALSE #don't show real-time progress
               )

Questa funzione produce il grafico seguente, che mostra il numero di predittori utilizzati in ciascuna divisione durante la costruzione degli alberi sull’asse x e l’errore out-of-bag stimato sull’asse y:

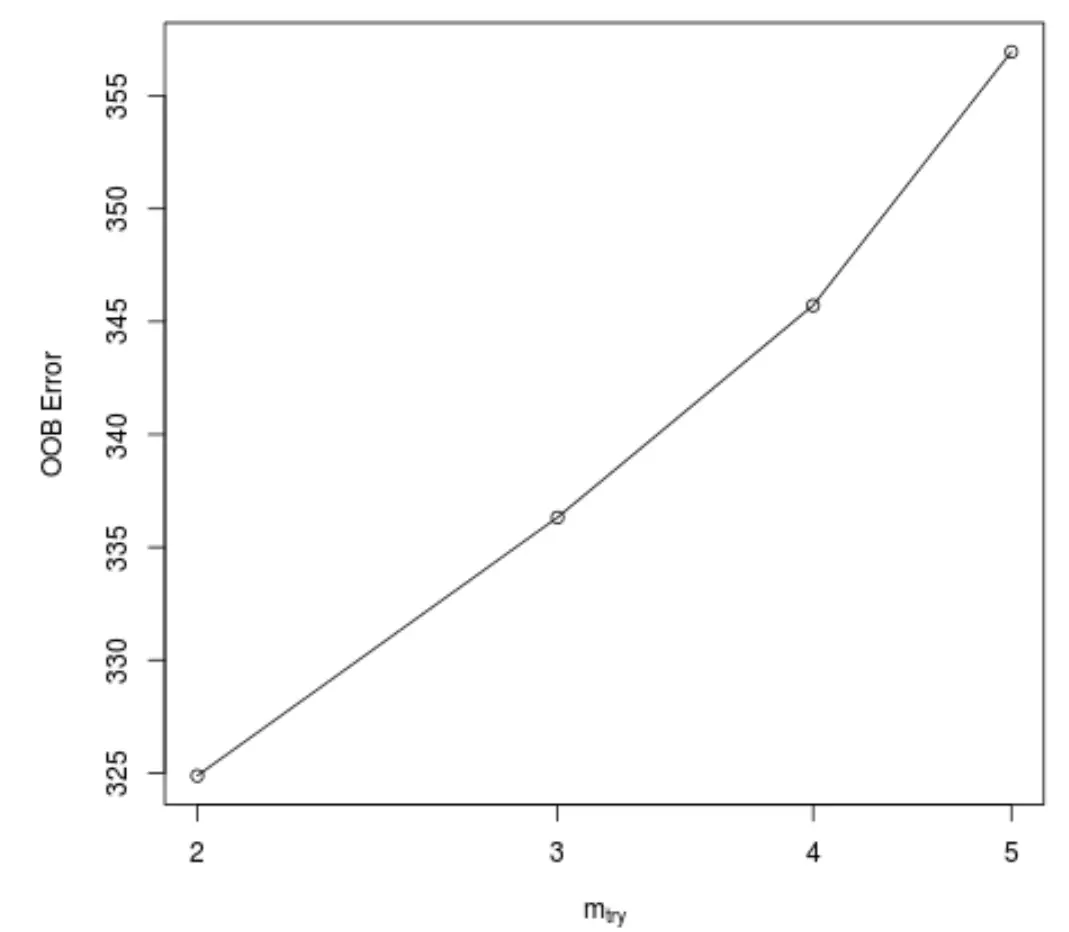
Possiamo vedere che l’errore OOB più basso si ottiene utilizzando 2 predittori scelti casualmente ad ogni divisione durante la costruzione degli alberi.

Ciò corrisponde in realtà all’impostazione predefinita (predittori totali/3 = 6/3 = 2) utilizzata dalla funzione randomForest() iniziale.

Passaggio 4: utilizzare il modello finale per fare previsioni

Infine, possiamo utilizzare il modello di foresta casuale adattato per fare previsioni su nuove osservazioni.

 #define new observation
new <- data.frame(Solar.R=150, Wind=8, Temp=70, Month=5, Day=5)

#use fitted bagged model to predict Ozone value of new observation
predict(model, newdata=new)

27.19442

Sulla base dei valori delle variabili predittive, il modello forestale casuale adattato prevede che il valore dell’ozono sarà 27,19442 in questo particolare giorno.

Il codice R completo utilizzato in questo esempio può essere trovato qui .