Come estrarre i residui dalla funzione lm() in r

È possibile utilizzare la seguente sintassi per estrarre i residui dalla funzione lm() in R:

 fit$residuals

Questo esempio presuppone che abbiamo utilizzato la funzione lm() per adattare un modello di regressione lineare e che abbiamo denominato i risultati fit .

L’esempio seguente mostra come utilizzare questa sintassi nella pratica.

Correlato:Come estrarre R-Squared dalla funzione lm() in R

Esempio: come estrarre i residui da lm() in R

Supponiamo di avere il seguente frame di dati in R che contiene informazioni sui minuti giocati, sui falli totali e sui punti totali segnati da 10 giocatori di basket:

 #create data frame
df <- data. frame (minutes=c(5, 10, 13, 14, 20, 22, 26, 34, 38, 40),
                 fouls=c(5, 5, 3, 4, 2, 1, 3, 2, 1, 1),
                 points=c(6, 8, 8, 7, 14, 10, 22, 24, 28, 30))

#view data frame
df

   minutes fouls points
1 5 5 6
2 10 5 8
3 13 3 8
4 14 4 7
5 20 2 14
6 22 1 10
7 26 3 22
8 34 2 24
9 38 1 28
10 40 1 30

Supponiamo di voler adattare il seguente modello di regressione lineare multipla:

punti = β ₀ + β ₁ (minuti) + β ₂ (falli)

Possiamo usare la funzione lm() per adattare questo modello di regressione:

 #fit multiple linear regression model
fit <- lm(points ~ minutes + fouls, data=df)

Possiamo quindi digitare fit$residuals per estrarre i residui dal modello:

 #extract residuals from model
fit$residuals

         1 2 3 4 5 6 7 
 2.0888729 -0.7982137 0.6371041 -3.5240982 1.9789676 -1.7920822 1.9306786 
         8 9 10 
-1.7048752 0.5692404 0.6144057

Poiché nel nostro database erano presenti 10 osservazioni in totale, ci sono 10 residui, uno per ciascuna osservazione.

Per esempio:

• La prima osservazione ha un residuo di 2.089 .
• La seconda osservazione ha un residuo di -0,798 .
• La terza osservazione ha un residuo di 0,637 .

E così via.

Se lo desideriamo, possiamo quindi creare un grafico dei residui rispetto ai valori adattati:

 #store residuals in variable
res <- fit$residuals

#produce residual vs. fitted plot
plot(fitted(fit), res)

#add a horizontal line at 0 
abline(0,0)

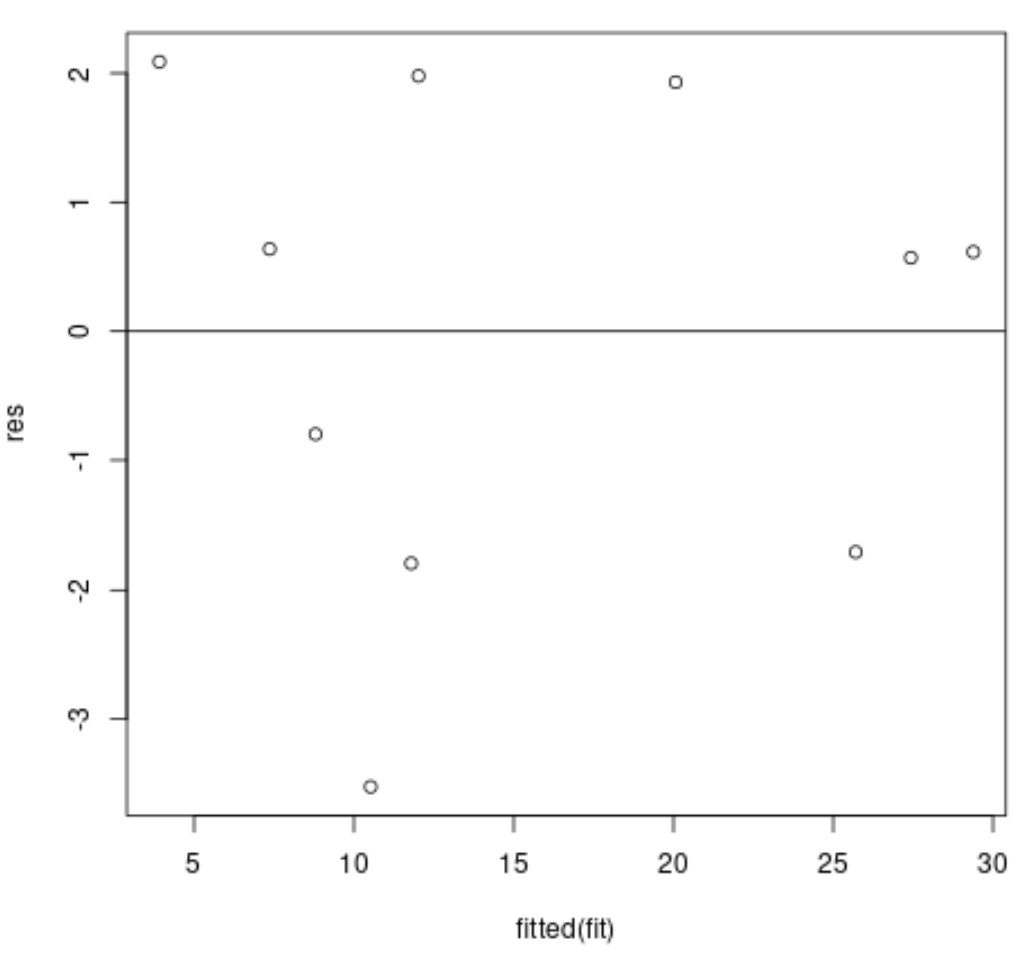
L’asse x mostra i valori adattati e l’asse y mostra i residui.

Idealmente, i residui dovrebbero essere sparsi in modo casuale attorno allo zero, senza uno schema chiaro, per garantire che il presupposto di omoschedasticità sia soddisfatto.

Nel grafico dei residui sopra, possiamo vedere che i residui sembrano essere sparsi in modo casuale attorno allo zero senza uno schema chiaro, il che significa che è probabile che l’ipotesi di omoschedasticità sia soddisfatta.

Risorse addizionali

I seguenti tutorial spiegano come eseguire altre attività comuni in R:

Come eseguire una regressione lineare semplice in R
Come eseguire la regressione lineare multipla in R
Come creare una trama residua in R