Cosa sono gli eventi disgiunti? (definizione ed esempi)

Gli eventi disgiunti sono eventi che non possono verificarsi contemporaneamente.

Scritti in notazione probabilistica, gli eventi A e B sono disgiunti se la loro intersezione è zero. Questo può essere scritto come segue:

• P(A e B) = 0
• P(A∩B) = 0

Ad esempio, supponiamo di selezionare una carta a caso da un mazzo. Sia l’evento A l’evento in cui la carta è picche o fiori e l’evento B l’evento in cui la carta è un cuore o un quadri.

Definiremo lo spazio campionario per gli eventi come segue:

• A = {Picca, Fiori}
• B = {Cuore, Diamante}

Si noti che non vi è alcuna sovrapposizione tra i due spazi campionati. Pertanto gli eventi A e B sono eventi disgiunti perché non possono verificarsi entrambi contemporaneamente.

Nota: si dice anche che gli eventi disgiunti si escludono a vicenda .

Esempi di eventi disgiunti

Ecco alcuni altri esempi di eventi disgiunti.

Esempio 1: pareggio

Supponiamo di lanciare una moneta. Sia l’evento A l’evento in cui la moneta esce testa e l’evento B l’evento in cui la moneta esce testa.

L’evento A e l’evento B sarebbero disgiunti perché non possono verificarsi entrambi contemporaneamente. La moneta non può cadere su testa o croce.

Esempio 2: lancio di dadi

Supponiamo di lanciare un dado. Sia l’evento A l’evento in cui il dado esce su un numero dispari e l’evento B l’evento in cui il dado esce su un numero pari.

L’evento A e l’evento B sarebbero disgiunti perché non possono verificarsi entrambi contemporaneamente. I dadi non possono cadere su un numero pari e su un numero dispari.

Esempio 3: posizione del Pro Bowl

Supponiamo che la NFL voglia scegliere un luogo per ospitare il Pro Bowl. Hanno ristretto le opzioni a Miami e San Diego. Mettono i due nomi in un cappello e ne scelgono uno a caso. Supponiamo che l’Evento A sia l’evento per cui selezionano Miami e l’Evento B è l’evento per cui selezionano San Diego.

L’evento A e l’evento B sarebbero disgiunti perché non possono verificarsi entrambi contemporaneamente. Sia Miami che San Diego non possono essere selezionate.

Visualizza eventi disgiunti

Un modo utile per visualizzare eventi disgiunti è creare un diagramma di Venn.

Se due eventi sono disgiunti , non si sovrapporranno affatto in un diagramma di Venn:

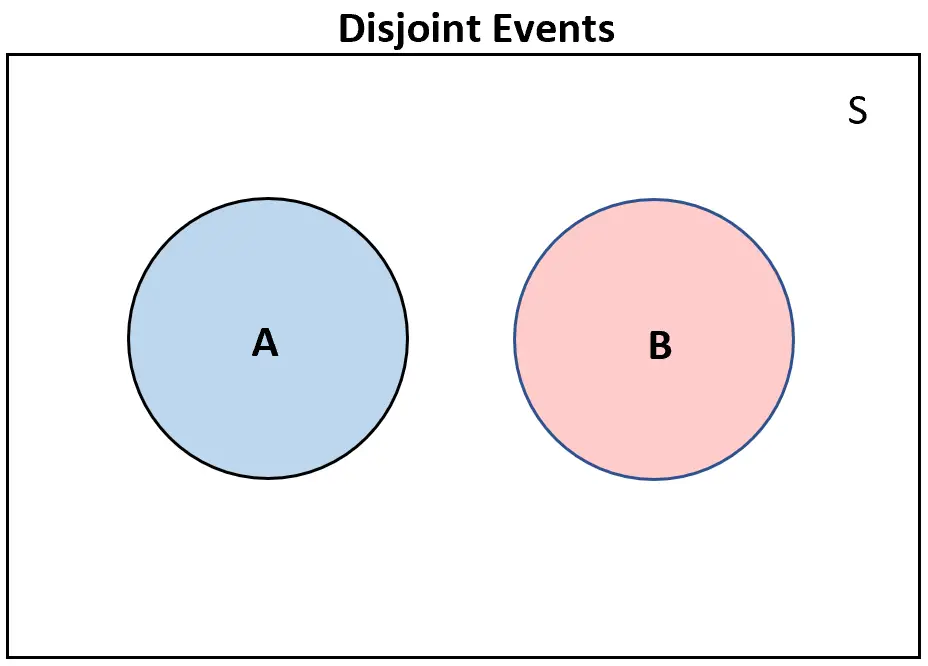
Viceversa, se due eventi non sono disgiunti , ci sarà almeno qualche sovrapposizione nel diagramma di Venn:

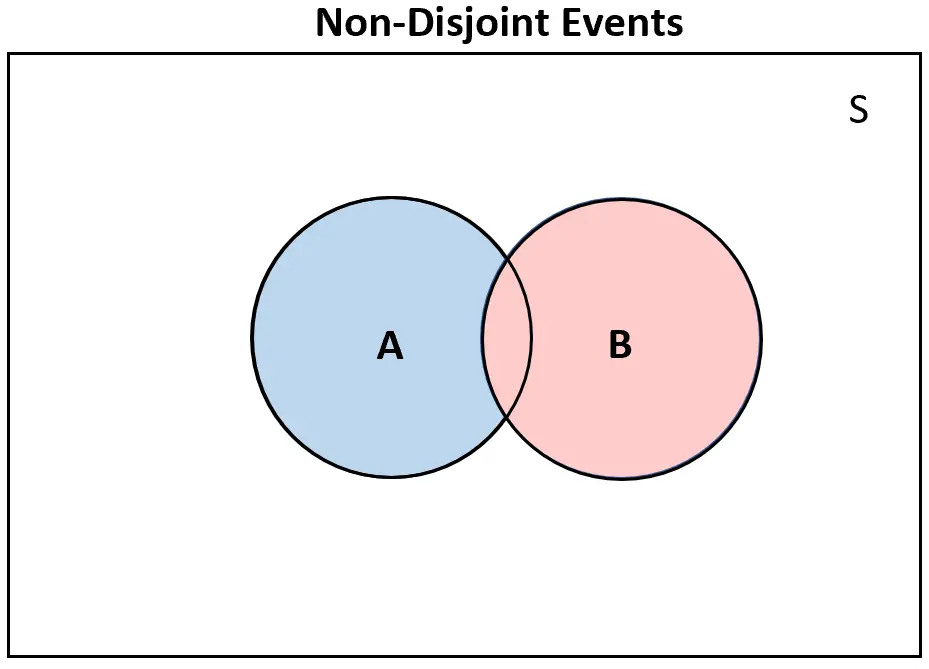
La probabilità di eventi disgiunti

Come accennato in precedenza, se due eventi sono disgiunti, la probabilità che si verifichino entrambi nello stesso momento è zero.

• P(A∩B) = 0

Allo stesso modo, la probabilità che si verifichi uno dei due eventi può essere calcolata sommando le rispettive probabilità individuali.

• P(A∪B) = P(A) + P(B)

Ad esempio, lascia che l’evento A sia l’evento in cui un dado esce su 1 o 2 e l’evento B sia l’evento in cui un dado esce su 5 o 6.

Definiremo lo spazio campionario per gli eventi come segue:

• A = {1, 2}
• B = {5, 6}

Calcoleremo la probabilità che si verifichi l’evento A o l’evento B come:

• P(A∪B) = P(A) + P(B)
• P(A∪B) = 2/6 + 2/6
• P(A∪B) = 4/6 = 2/3

La probabilità che si verifichi l’evento A o l’evento B è 2/3 .

Risorse addizionali

I seguenti tutorial forniscono spiegazioni su altri argomenti comuni relativi alla probabilità:

Come trovare la probabilità di A o B: con esempi
Come trovare la probabilità di A e B: con esempi
Legge della probabilità totale: definizione ed esempi