Excel: come utilizzare regr.lin per eseguire regressioni lineari multiple

È possibile utilizzare la funzione REGR.LIN in Excel per adattare un modello di regressione lineare multipla a un set di dati.

Questa funzione utilizza la seguente sintassi di base:

 = LINEST ( known_y's, [known_x's], [const], [stats] )

Oro:

• y_nota : un array di valori y noti
• x_conosciuti : un array di valori x noti
• const : argomento facoltativo. Se TRUE, la costante b viene elaborata normalmente. Se FALSE, la costante b è impostata su 1.
• stats : argomento facoltativo. Se TRUE, vengono restituite statistiche di regressione aggiuntive. Se FALSE, non vengono restituite statistiche di regressione aggiuntive.

Il seguente esempio passo passo mostra come utilizzare questa funzione nella pratica.

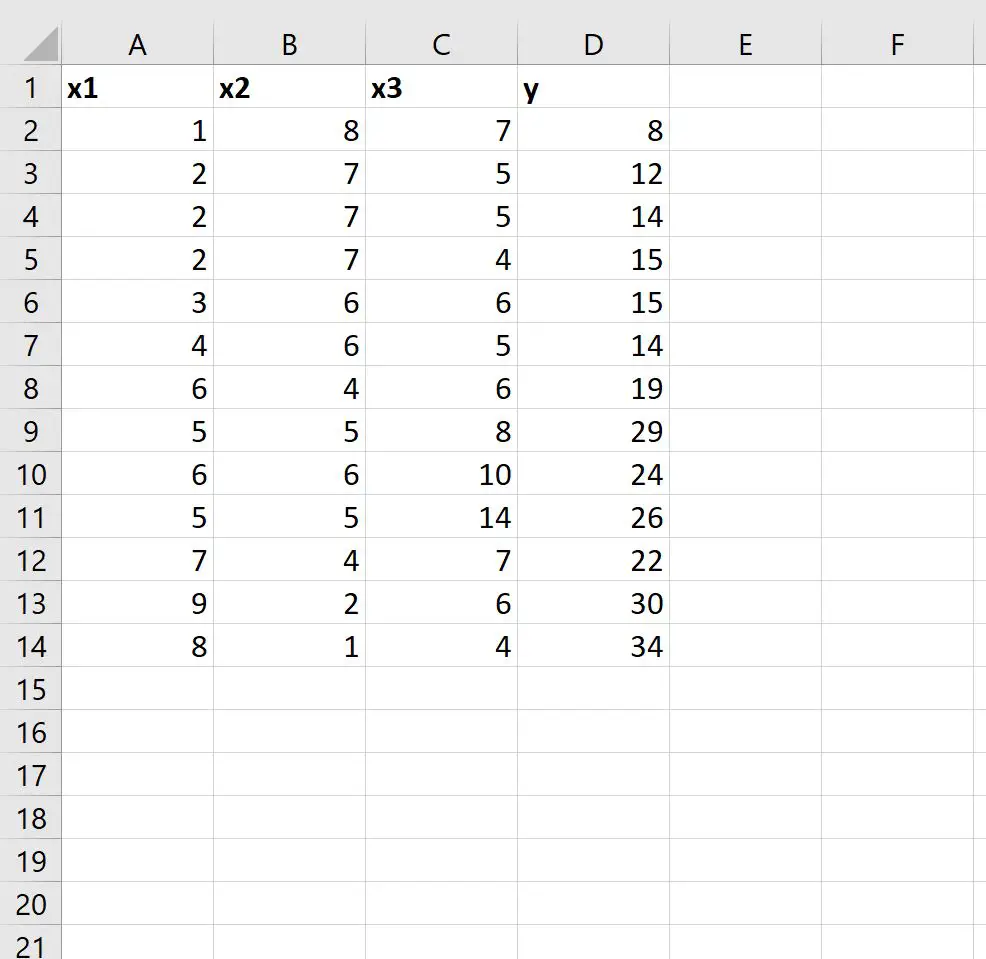
Passaggio 1: inserisci i dati

Innanzitutto, inseriamo il seguente set di dati in Excel:

Passaggio 2: utilizzare REGR.LIN per adattare un modello di regressione lineare multipla

Supponiamo di voler adattare un modello di regressione lineare multipla utilizzando x1 , x2 e x3 come variabili predittive e y come variabile di risposta.

Per fare ciò, possiamo digitare la seguente formula in qualsiasi cella per adattarla a questo modello di regressione lineare multipla

 =LINEST( D2:D14 , A2:C14 )

Lo screenshot seguente mostra come utilizzare questa formula nella pratica:

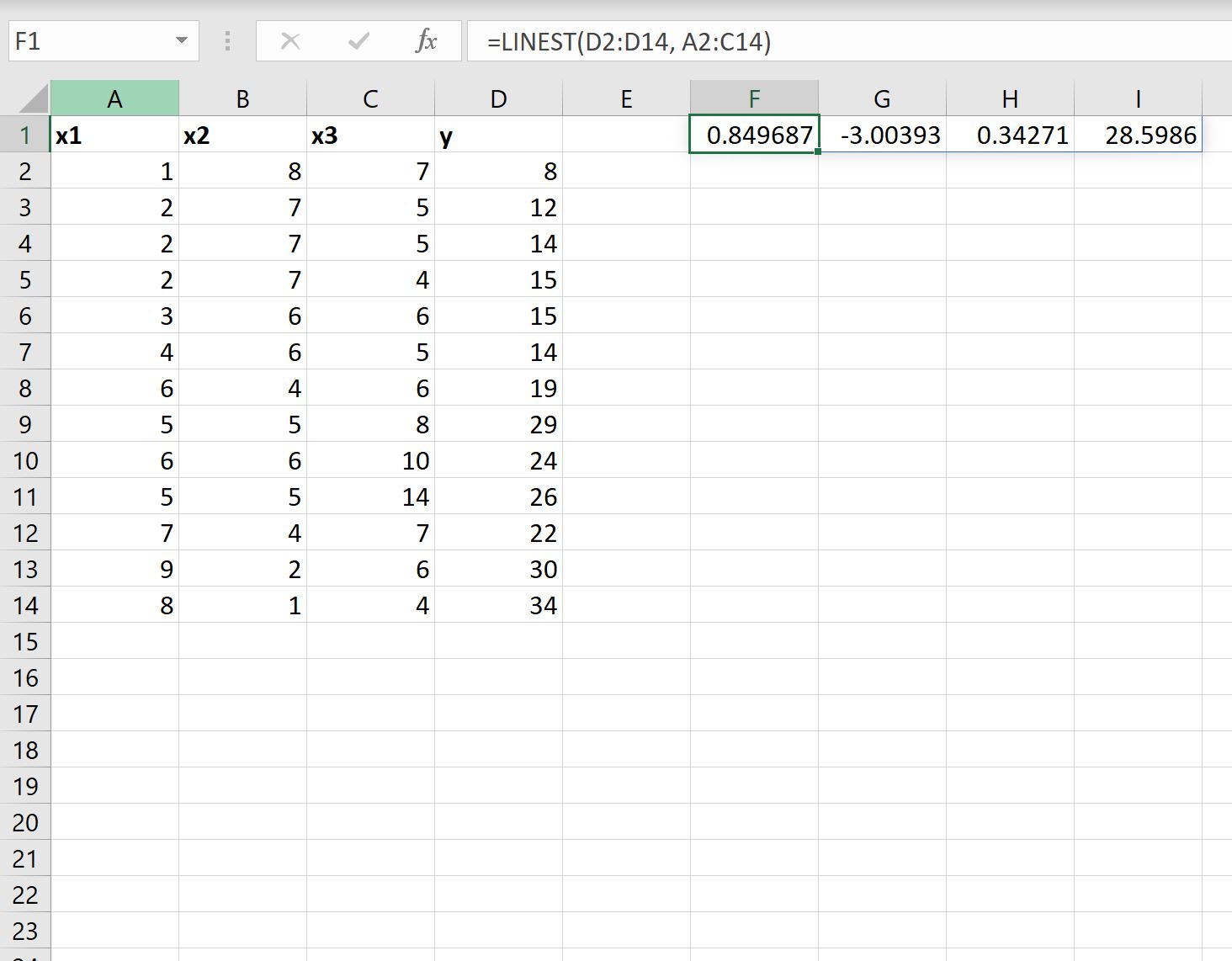
Ecco come interpretare il risultato:

• Il coefficiente dell’intercetta è 28.5986 .
• Il coefficiente per x1 è 0,34271 .
• Il coefficiente per x2 è -3.00393 .
• Il coefficiente per x3 è 0,849687 .

Utilizzando questi coefficienti, possiamo scrivere l’equazione di regressione adattata come segue:

y = 28,5986 + 0,34271(x1) – 3,00393(x2) + 0,849687(x3)

Passaggio 3 (facoltativo): visualizzare ulteriori statistiche di regressione

Possiamo anche impostare il valore dell’argomento stats nella funzione REGR.LIN uguale a VERO per visualizzare ulteriori statistiche di regressione per l’equazione di regressione adattata:

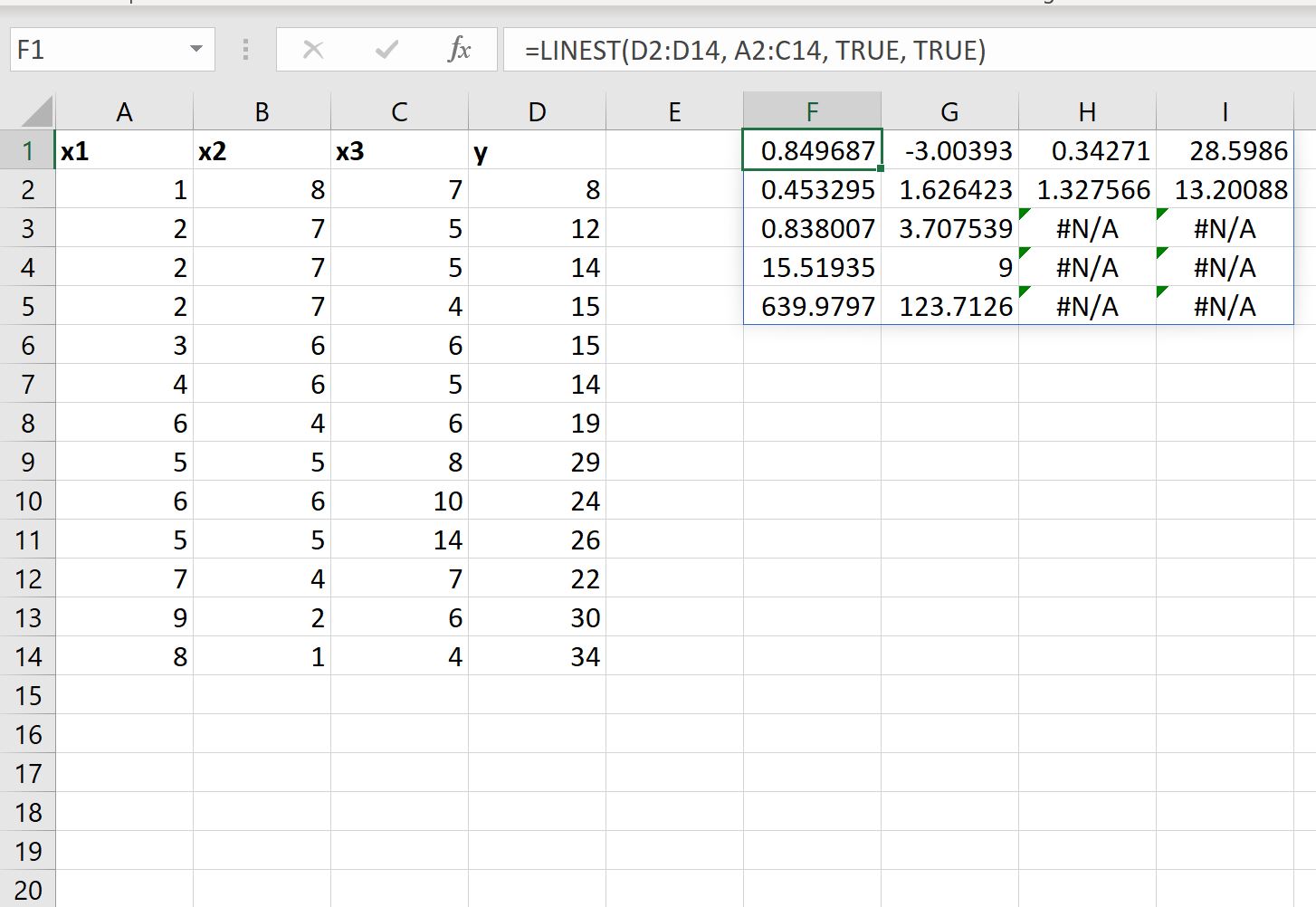
L’equazione di regressione adattata è sempre la stessa:

y = 28,5986 + 0,34271(x1) – 3,00393(x2) + 0,849687(x3)

Ecco come interpretare gli altri valori del risultato:

• L’errore standard per x3 è 0.453295 .
• L’errore standard per x2 è 1.626423 .
• L’errore standard per x1 è 1.327566 .
• L’errore standard per l’intercetta è 13.20088 .
• La R ² del modello è .838007 .
• L’errore standard residuo per y è 3,707539 .
• La statistica F complessiva è 15.51925 .
• I gradi di libertà sono 9 .
• La somma dei quadrati della regressione è 639.9797 .
• La somma residua dei quadrati è 123.7126 .

In generale, la misura di maggior interesse in queste statistiche aggiuntive è il valore ^R2 , che rappresenta la proporzione della varianza nella variabile di risposta che può essere spiegata dalla variabile predittrice.

Il valore di ^R2 può variare da 0 a 1.

Poiché l’R ² di questo particolare modello è 0,838 , ciò ci dice che le variabili predittive stanno facendo un buon lavoro nel prevedere il valore della variabile di risposta y.

Correlato: Qual è un buon valore R quadrato?

Risorse addizionali

I seguenti tutorial spiegano come eseguire altre operazioni comuni in Excel:

Come utilizzare la funzione REGR.LOG in Excel
Come eseguire la regressione non lineare in Excel
Come eseguire la regressione cubica in Excel