Come calcolare gli intervalli di confidenza in fogli google

Un intervallo di confidenza per una media è un intervallo di valori che probabilmente contiene la media della popolazione con un certo livello di confidenza.

Viene calcolato come segue:

Intervallo di confidenza = x +/- t*(s/√ n )

Oro:

• x : media campionaria
• t: valore t che corrisponde al livello di confidenza
• s: deviazione standard campionaria
• n: dimensione del campione

Questo tutorial spiega come calcolare gli intervalli di confidenza in Fogli Google.

Intervalli di confidenza utilizzando la distribuzione t

Se stiamo lavorando con un campione piccolo (n < 30), possiamo utilizzare la distribuzione t per calcolare un intervallo di confidenza per la media della popolazione.

Ad esempio, supponiamo di voler calcolare un intervallo di confidenza per l’altezza media reale della popolazione (in pollici) di una determinata specie di piante, utilizzando un campione di 15 piante:

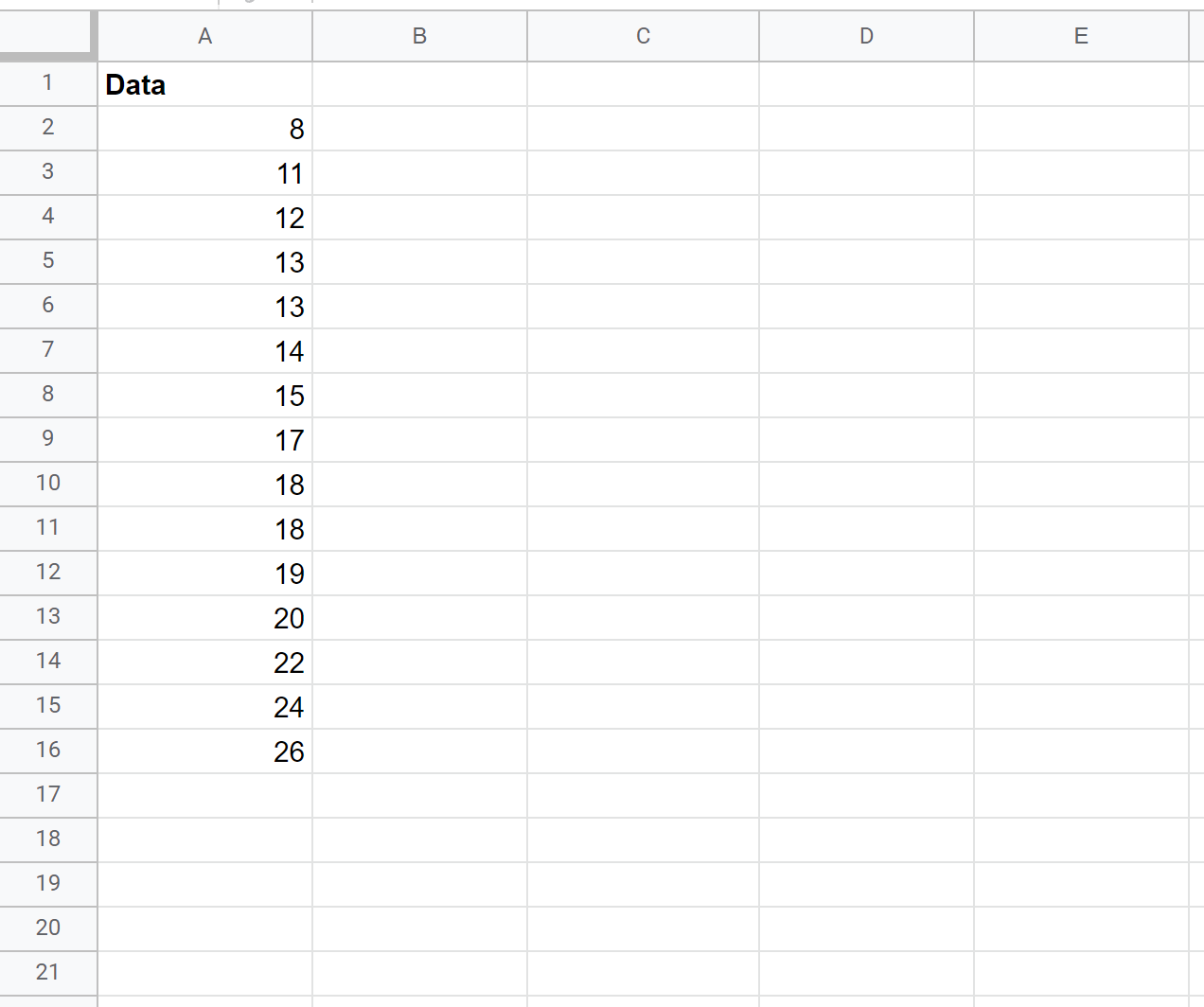
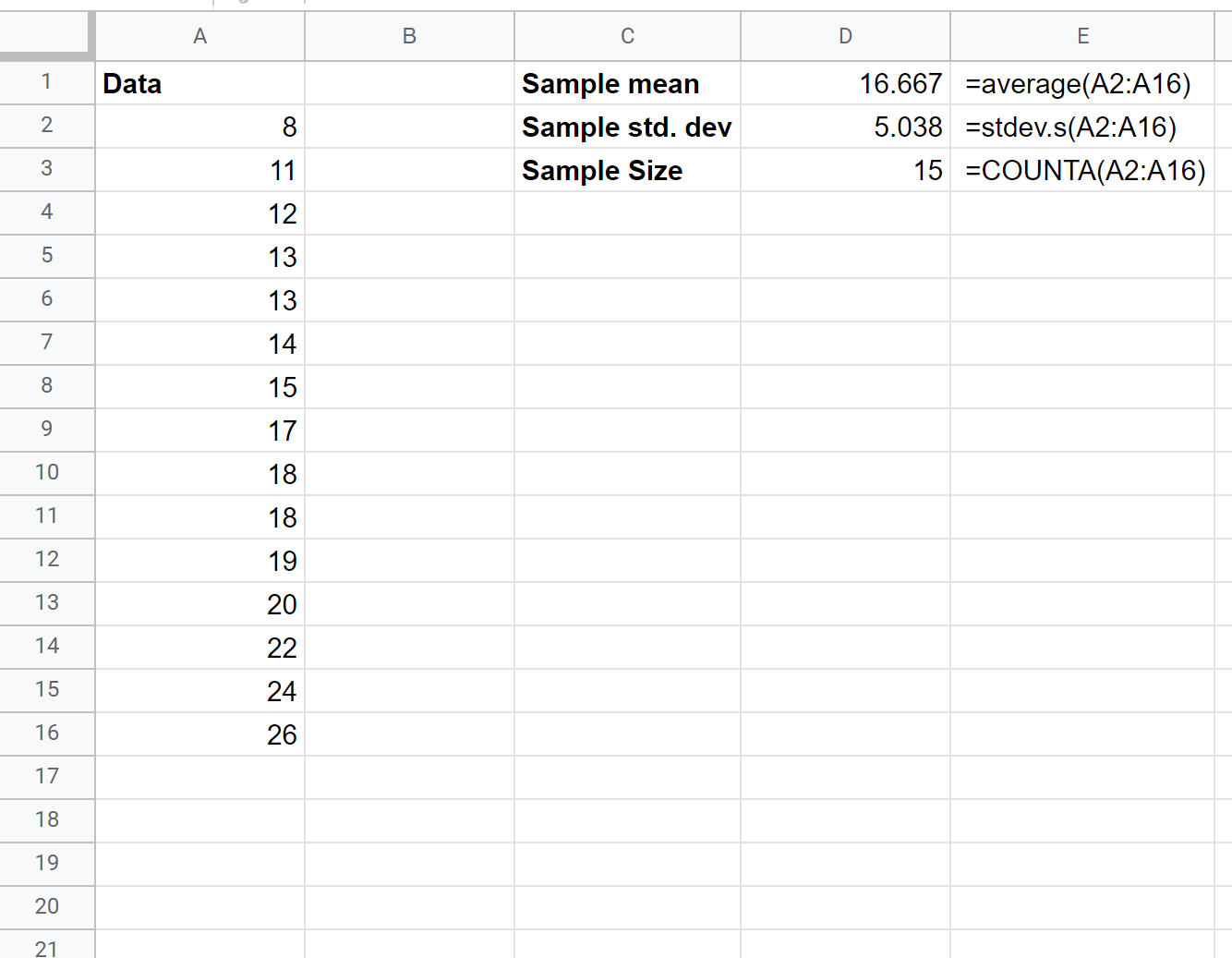
Innanzitutto, possiamo calcolare la media campionaria, la deviazione standard campionaria e la dimensione del campione:

Quindi possiamo utilizzare le seguenti formule per calcolare il limite inferiore e superiore dell’intervallo di confidenza al 95%:

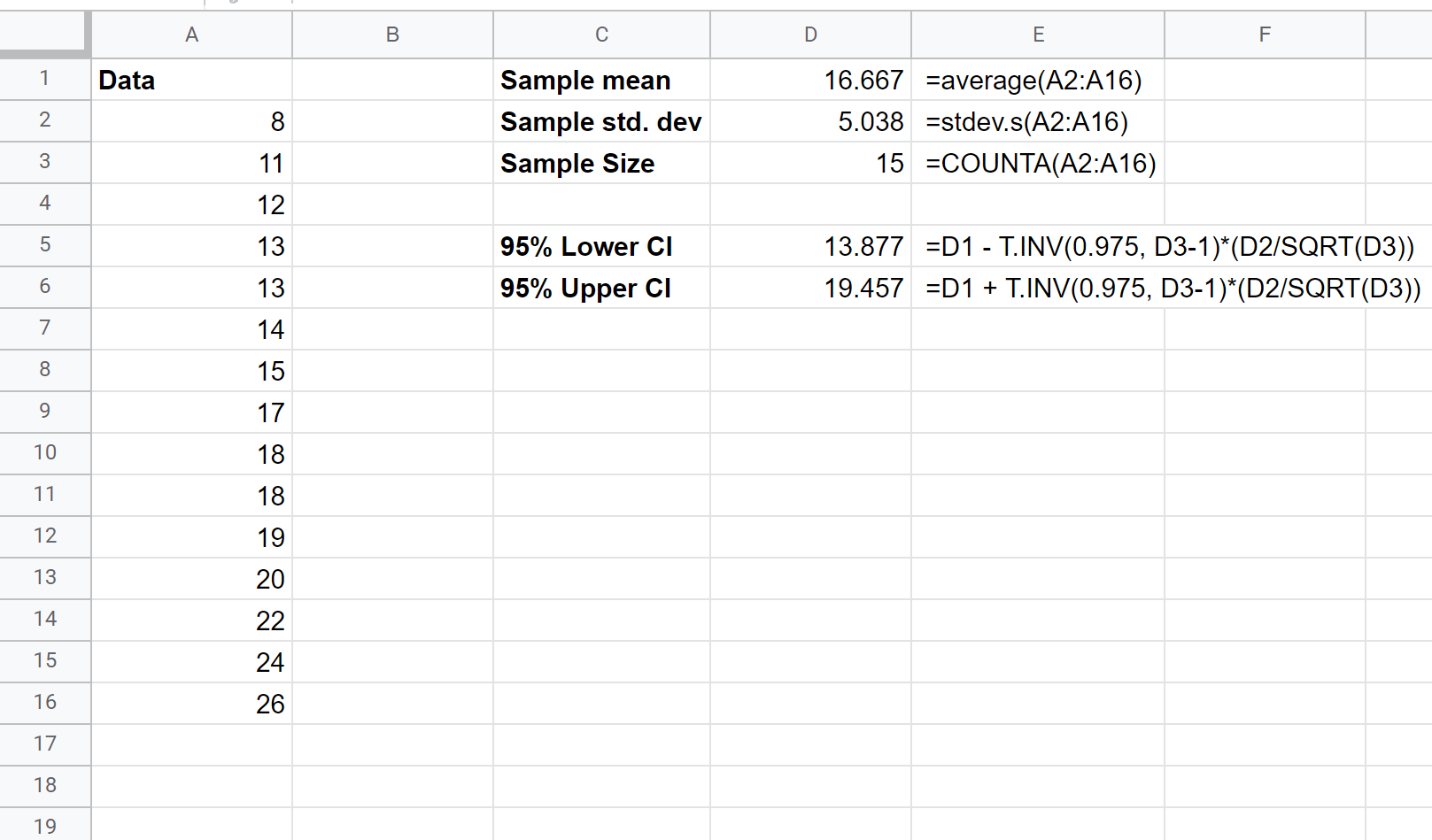
L’intervallo di confidenza al 95% per la dimensione media reale della popolazione è (13,877, 19,457) .

Intervalli di confidenza utilizzando la distribuzione normale

Se lavoriamo con campioni più grandi (n≥30), possiamo assumere che la distribuzione campionaria della media campionaria sia normalmente distribuita grazie al teorema del limite centrale .

Ciò significa che possiamo invece utilizzare la funzione NORM.S.INV() per calcolare il valore critico da utilizzare per l’intervallo di confidenza.

L’esempio seguente mostra come calcolare un intervallo di confidenza per l’altezza media reale della popolazione (in pollici) di una determinata specie di piante, utilizzando un campione di 30 piante:

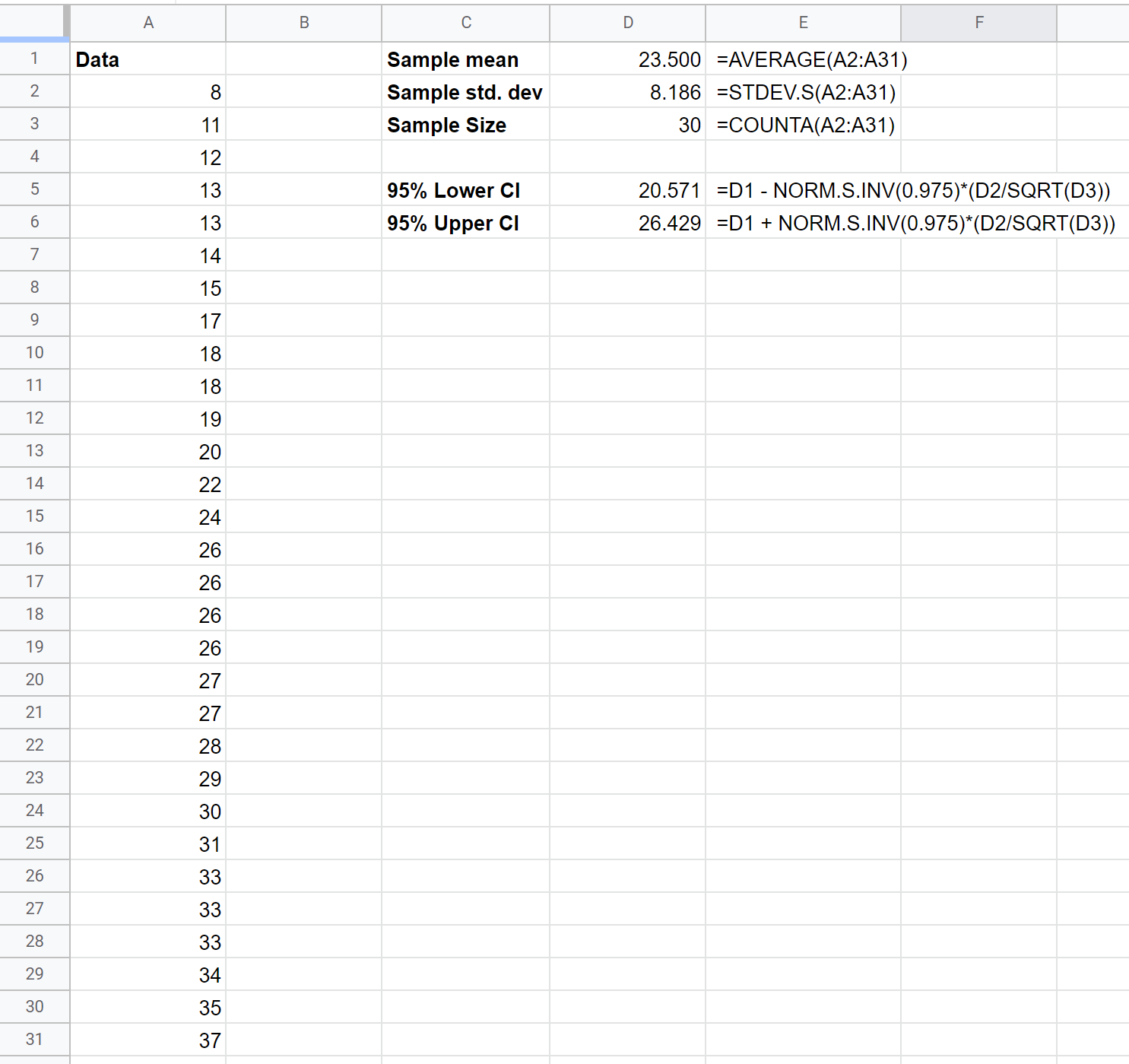
L’intervallo di confidenza al 95% per la dimensione media reale della popolazione è (20.571, 26.429) .

Si noti che livelli di confidenza più elevati portano a intervalli di confidenza più ampi. Ad esempio, ecco come calcolare un CI del 99% per gli stessi identici dati:

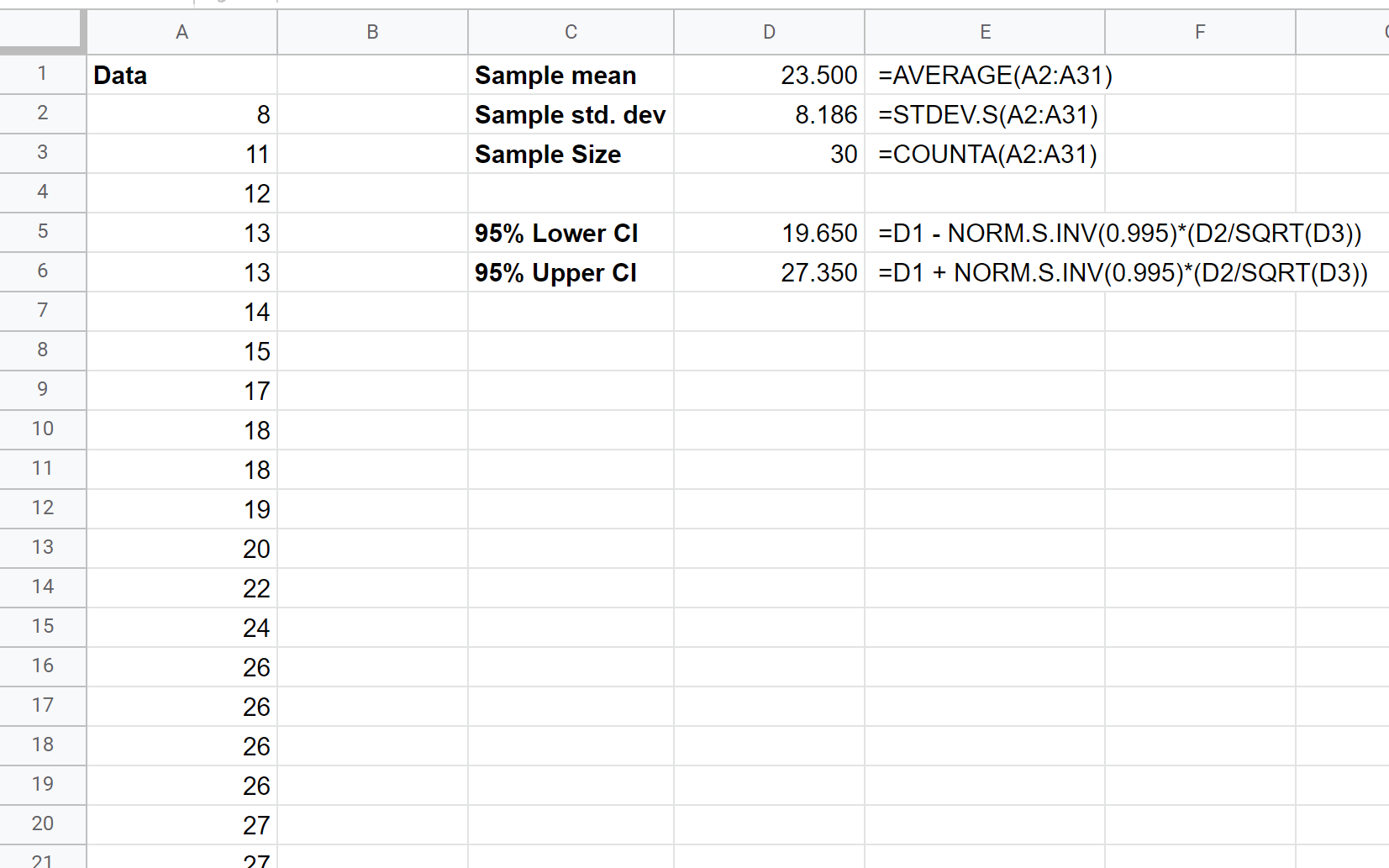
L’intervallo di confidenza al 99% per la dimensione media reale della popolazione è (19.650, 27.350) .

Si noti che questo intervallo di confidenza del 99% è più ampio dell’intervallo di confidenza del 95% calcolato in precedenza.

Correlato: Livello di confidenza vs. Intervallo di confidenza: qual è la differenza?

Risorse addizionali

I seguenti tutorial spiegano come calcolare gli intervalli di confidenza utilizzando altri software statistici:

Come calcolare gli intervalli di confidenza in Excel
Come calcolare gli intervalli di confidenza in R
Come calcolare gli intervalli di confidenza in Python