Come calcolare la correlazione del rango di spearman in fogli google

In statistica, la correlazione si riferisce alla forza e alla direzione di una relazione tra due variabili. Il valore di un coefficiente di correlazione può variare da -1 a 1, con le seguenti interpretazioni:

• -1: una perfetta relazione negativa tra due variabili
• 0: nessuna relazione tra due variabili
• 1: una perfetta relazione positiva tra due variabili

Un tipo speciale di correlazione è chiamata correlazione per rango di Spearman , che viene utilizzata per misurare la correlazione tra due variabili classificate. (ad esempio, la posizione del punteggio dell’esame di matematica di uno studente rispetto alla posizione del punteggio dell’esame di scienze in una classe).

Questo tutorial spiega come calcolare la correlazione del rango di Spearman tra due variabili in Fogli Google.

Esempio: correlazione del rango di Spearman in Fogli Google

Eseguire i passaggi seguenti per calcolare la correlazione del rango di Spearman tra il punteggio dell’esame di matematica e il punteggio dell’esame di scienze di 10 studenti in una classe particolare.

Passaggio 1: inserisci i dati.

Inserisci i risultati dell’esame di ogni studente in due colonne separate:

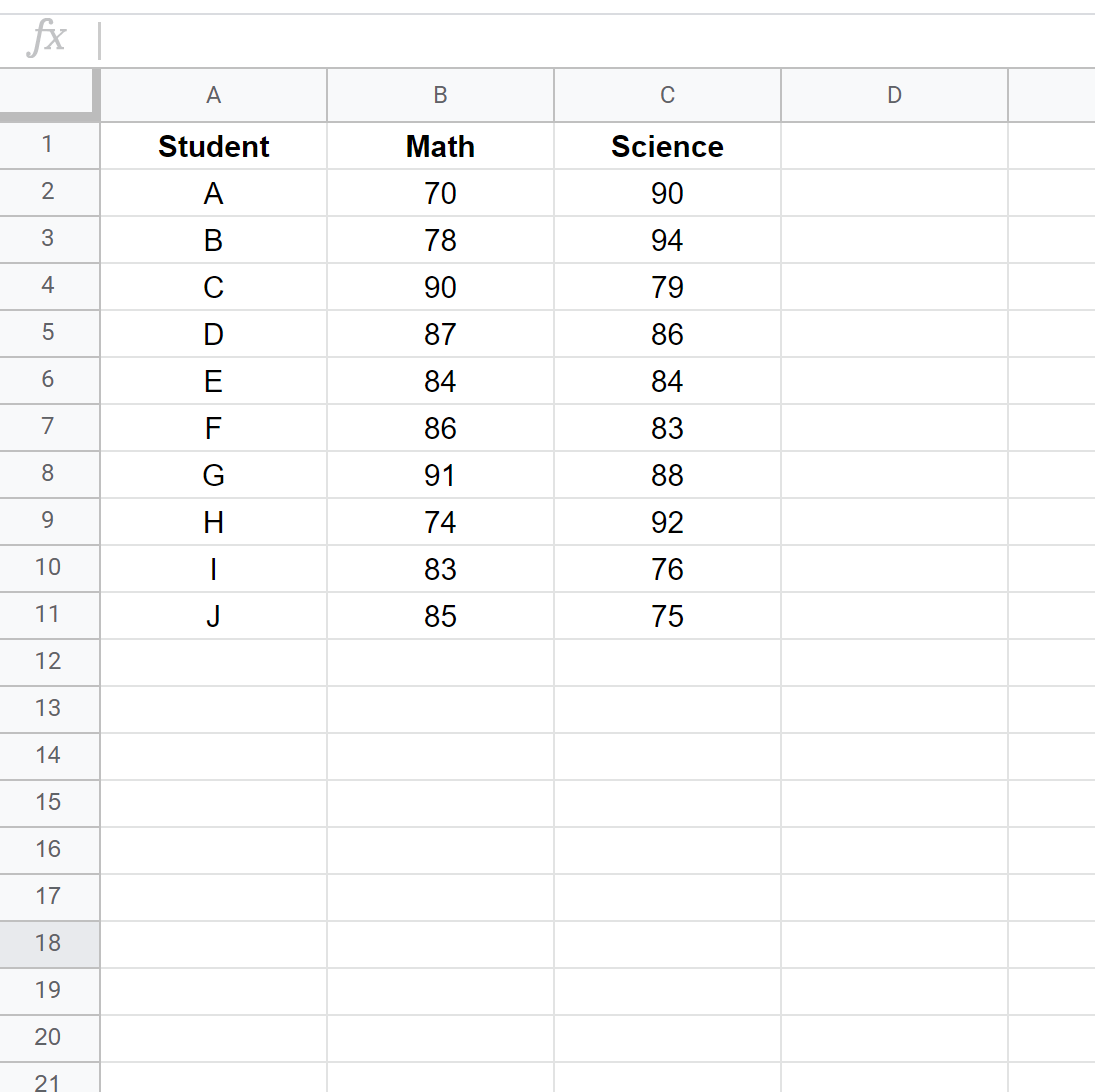
Passaggio 2: calcolare la classifica per ciascun punteggio dell’esame.

Successivamente, calcoleremo la classifica per ciascun punteggio dell’esame. Utilizza le seguenti formule nelle celle D2 ed E2 per calcolare i voti in matematica e scienze del primo studente:

Cella D2: =RANGO.MEDIA(B2, $B$2:$B$11, 0)

Cella E2: =RANGO.AVG(C2, $C$2:$C$11, 0)

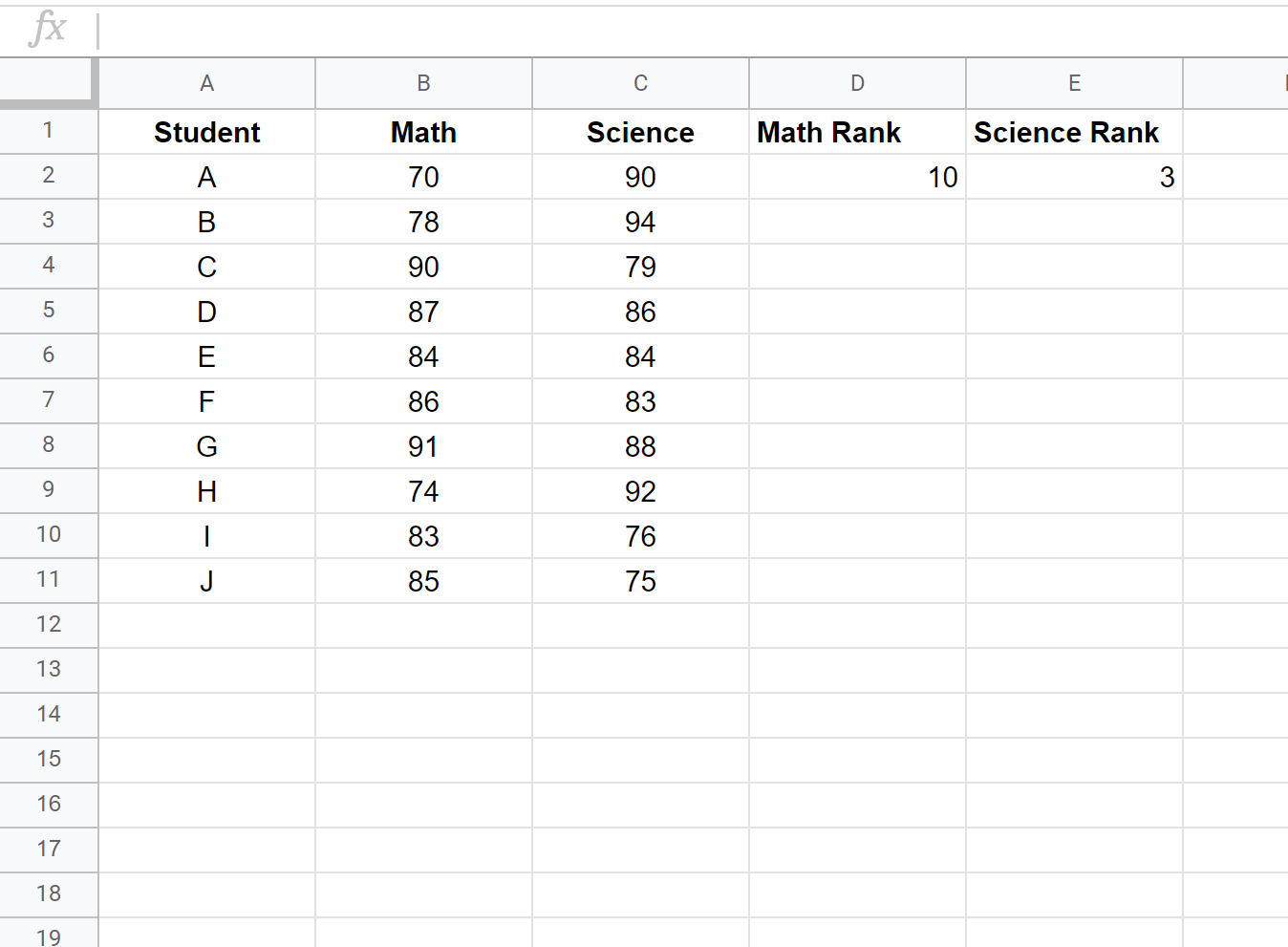
Successivamente, evidenzia le celle rimanenti da riempire:

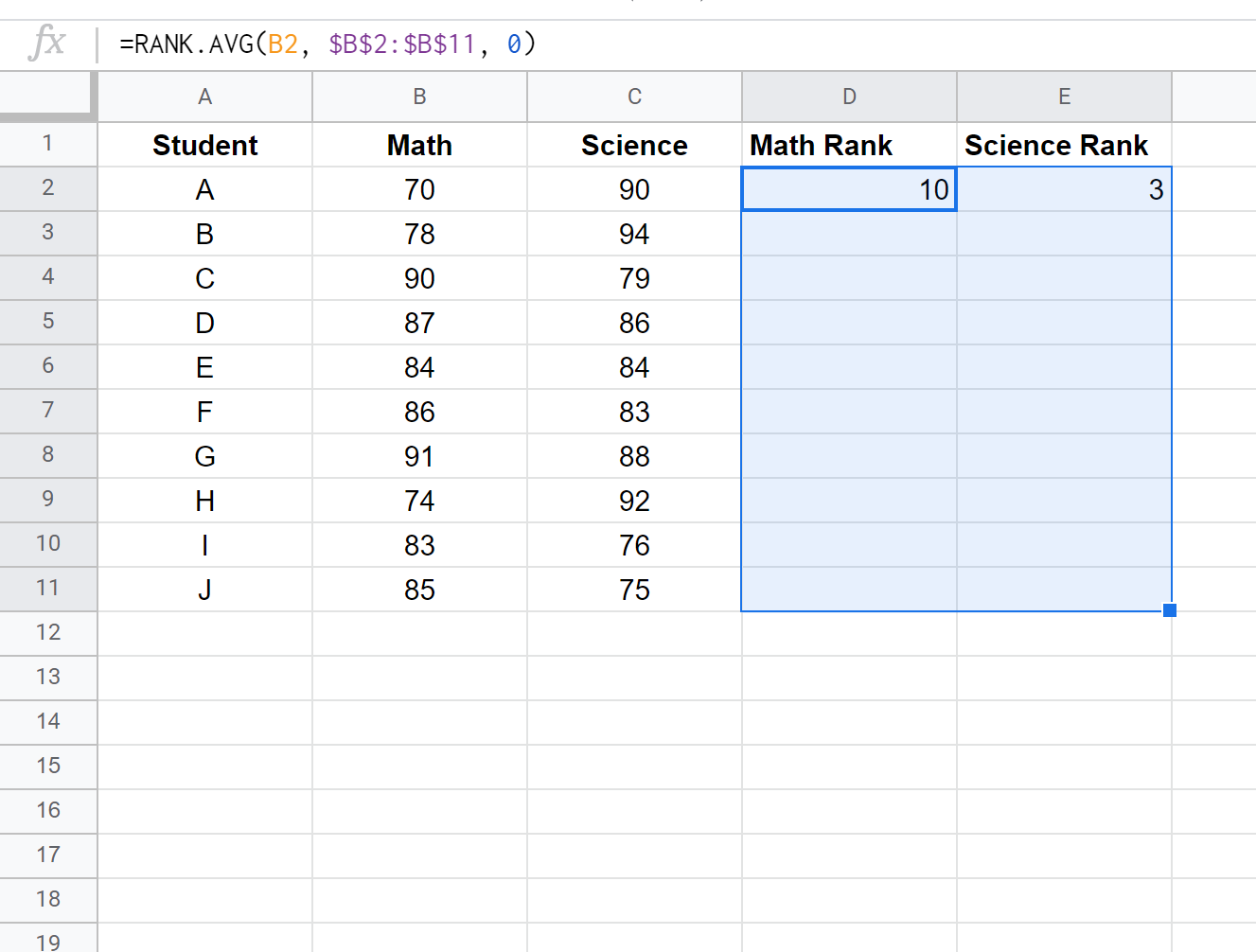
Clicca poi su Ctrl+D per inserire le graduatorie di ogni studente:

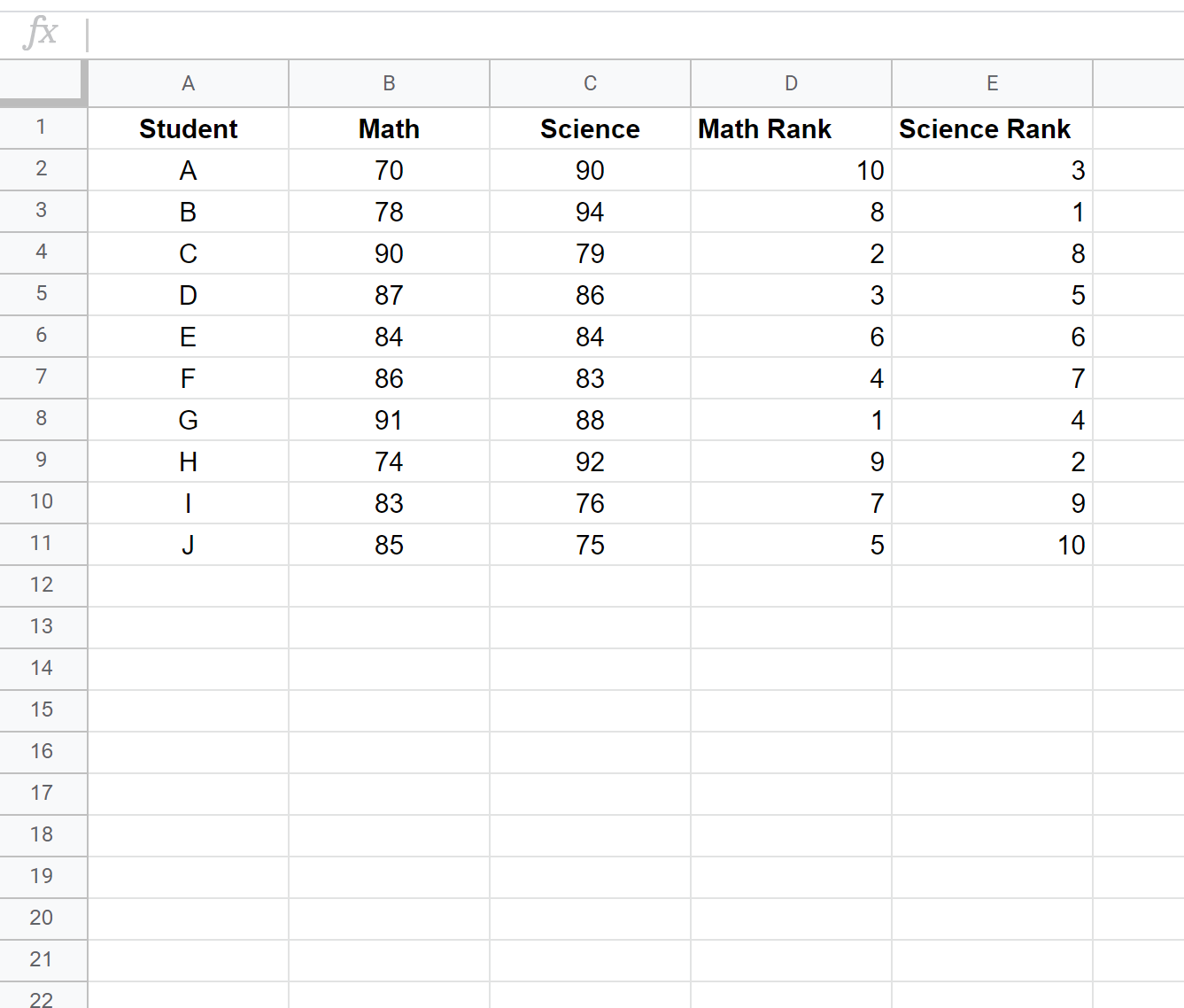
Passaggio 3: calcolare il coefficiente di correlazione del rango di Spearman.

Infine, calcoleremo il coefficiente di correlazione del rango di Spearman tra i punteggi di matematica e quelli di scienze utilizzando la funzione CORREL() :

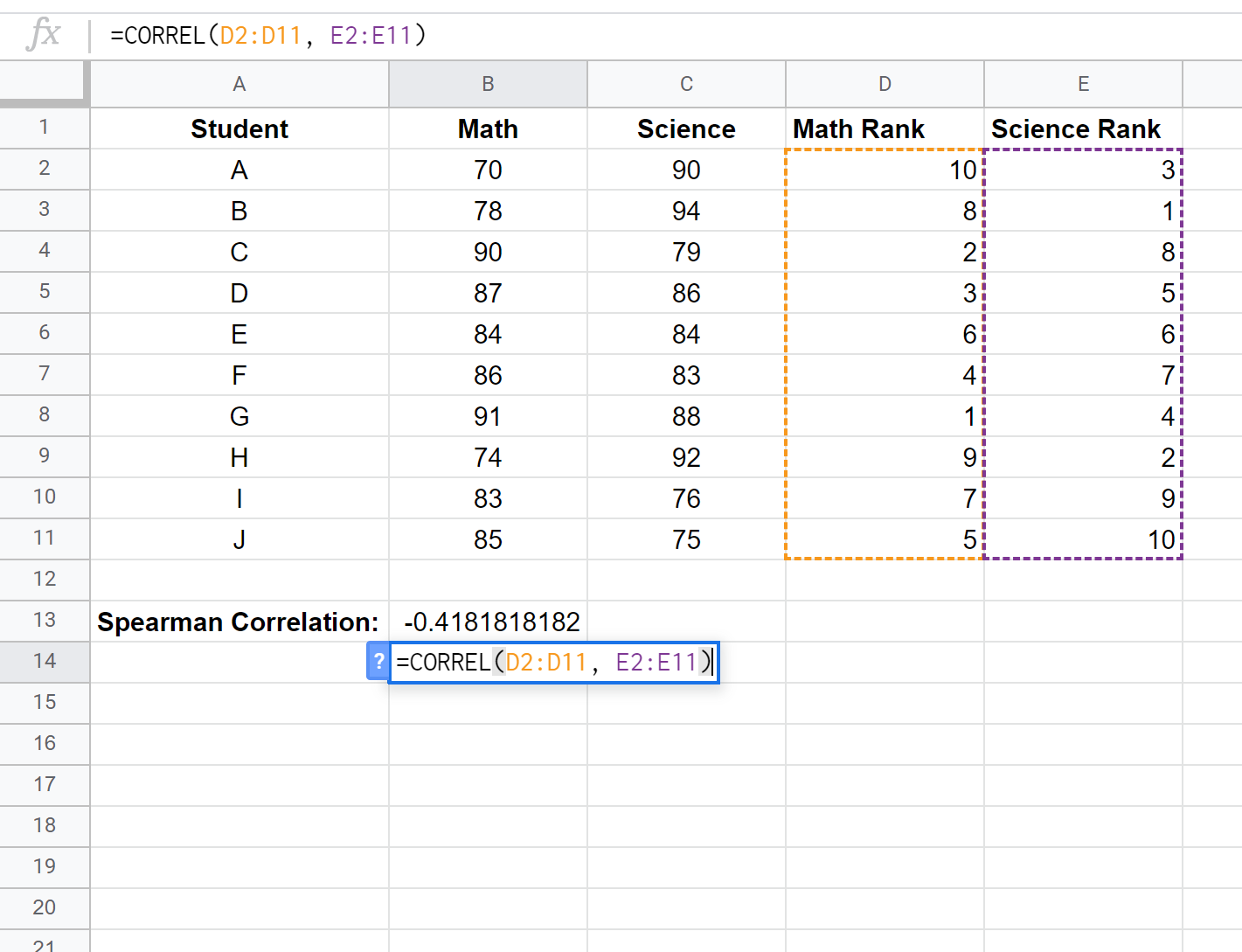
La correlazione del rango di Spearman risulta essere -0,41818 .

Passaggio 4 (facoltativo): determinare se la correlazione del rango di Spearman è statisticamente significativa.

Nel passaggio precedente, abbiamo scoperto che la correlazione del rango di Spearman tra i punteggi degli esami di matematica e scienze era -0,41818 , indicando una correlazione negativa tra le due variabili.

Tuttavia, per determinare se questa correlazione è statisticamente significativa, dovremmo fare riferimento a una tabella di correlazione dei valori critici dei ranghi di Spearman, che mostra i valori critici associati a diverse dimensioni del campione (n) e livelli di significatività (α).

Se il valore assoluto del nostro coefficiente di correlazione è maggiore del valore critico nella tabella, allora la correlazione tra le due variabili è statisticamente significativa.

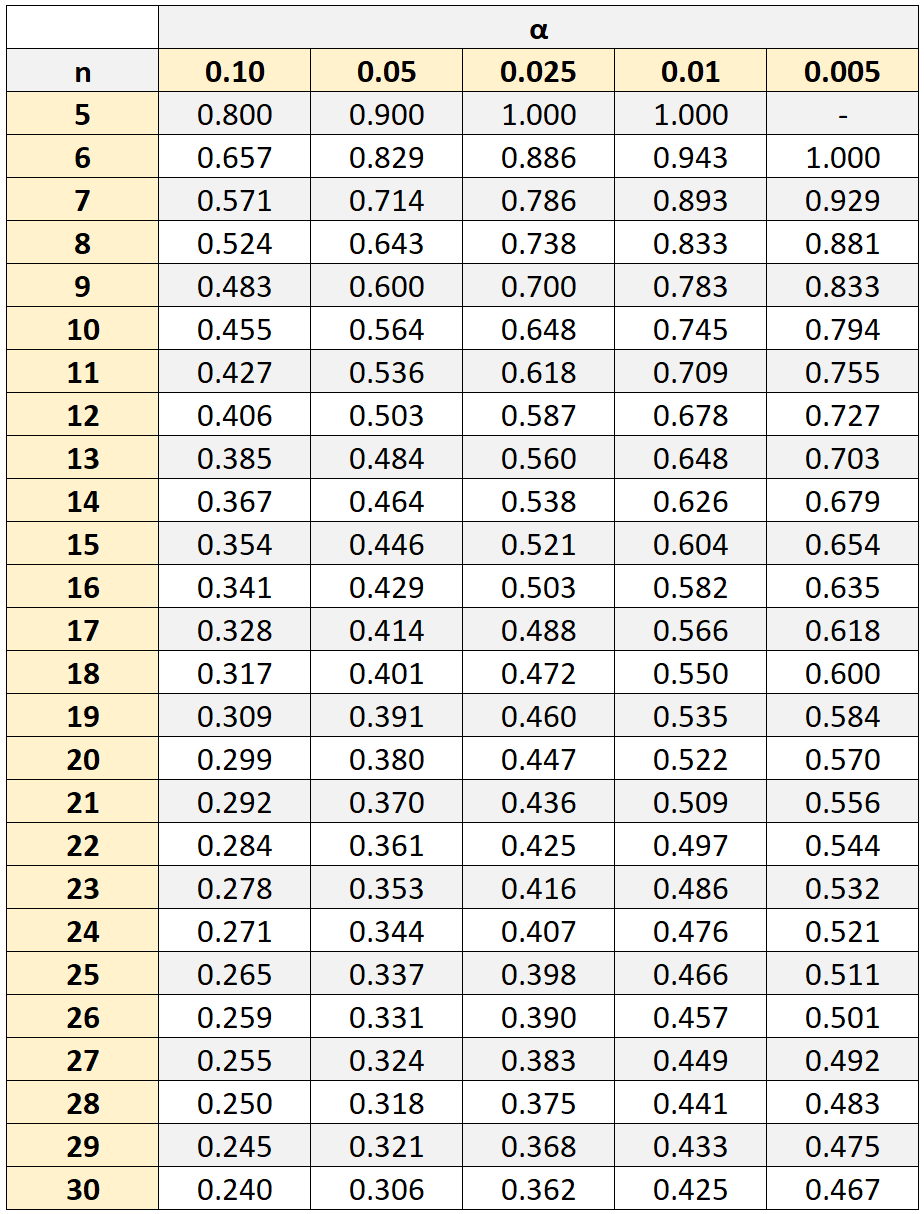
Nel nostro esempio, la dimensione del campione era n = 10 studenti. Utilizzando un livello di significatività pari a 0,05, troviamo che il valore critico è 0,564 .

Poiché il valore assoluto del coefficiente di correlazione del rango di Spearman che abbiamo calcolato ( 0,41818 ) non è maggiore di questo valore critico, ciò significa che la correlazione tra i punteggi di matematica e scienze non è statisticamente significativa.

Correlati: Come calcolare la correlazione del rango di Spearman in Excel