Come eseguire la regressione lineare in fogli google

La regressione lineare è un metodo che può essere utilizzato per quantificare la relazione tra una o più variabili esplicative e una variabile di risposta .

Usiamo la regressione lineare semplice quando è presente una sola variabile esplicativa e la regressione lineare multipla quando sono presenti due o più variabili esplicative.

Entrambi i tipi di regressione possono essere eseguiti utilizzando la funzione LINEST() di Fogli Google, che utilizza la seguente sintassi:

REGR.LIN (dati_noti_y, dati_noti_x, calcola_b, dettagliato)

Oro:

• known_data_y: array di valori di risposta
• known_data_x: tabella dei valori esplicativi
• calcola_b: indica se calcolare o meno l’intercetta. Questo è VERO per impostazione predefinita e lo lasciamo così per la regressione lineare.
• verbose: indica se fornire o meno statistiche di regressione aggiuntive oltre alla semplice pendenza e intercetta. Per impostazione predefinita è FALSO, ma specificheremo che è VERO nei nostri esempi.

I seguenti esempi mostrano come utilizzare questa funzione nella pratica.

Regressione lineare semplice in Fogli Google

Supponiamo di voler comprendere la relazione tra ore studiate e risultati degli esami. studiare per un esame e il voto ottenuto all’esame.

Per esplorare questa relazione, possiamo eseguire una semplice regressione lineare utilizzando le ore studiate come variabile esplicativa e i punteggi degli esami come variabile di risposta.

La schermata seguente mostra come eseguire una regressione lineare semplice utilizzando un set di dati di 20 studenti con la seguente formula utilizzata nella cella D2:

= LINEA ( B2:B21 , A2:A21 , VERO , VERO )

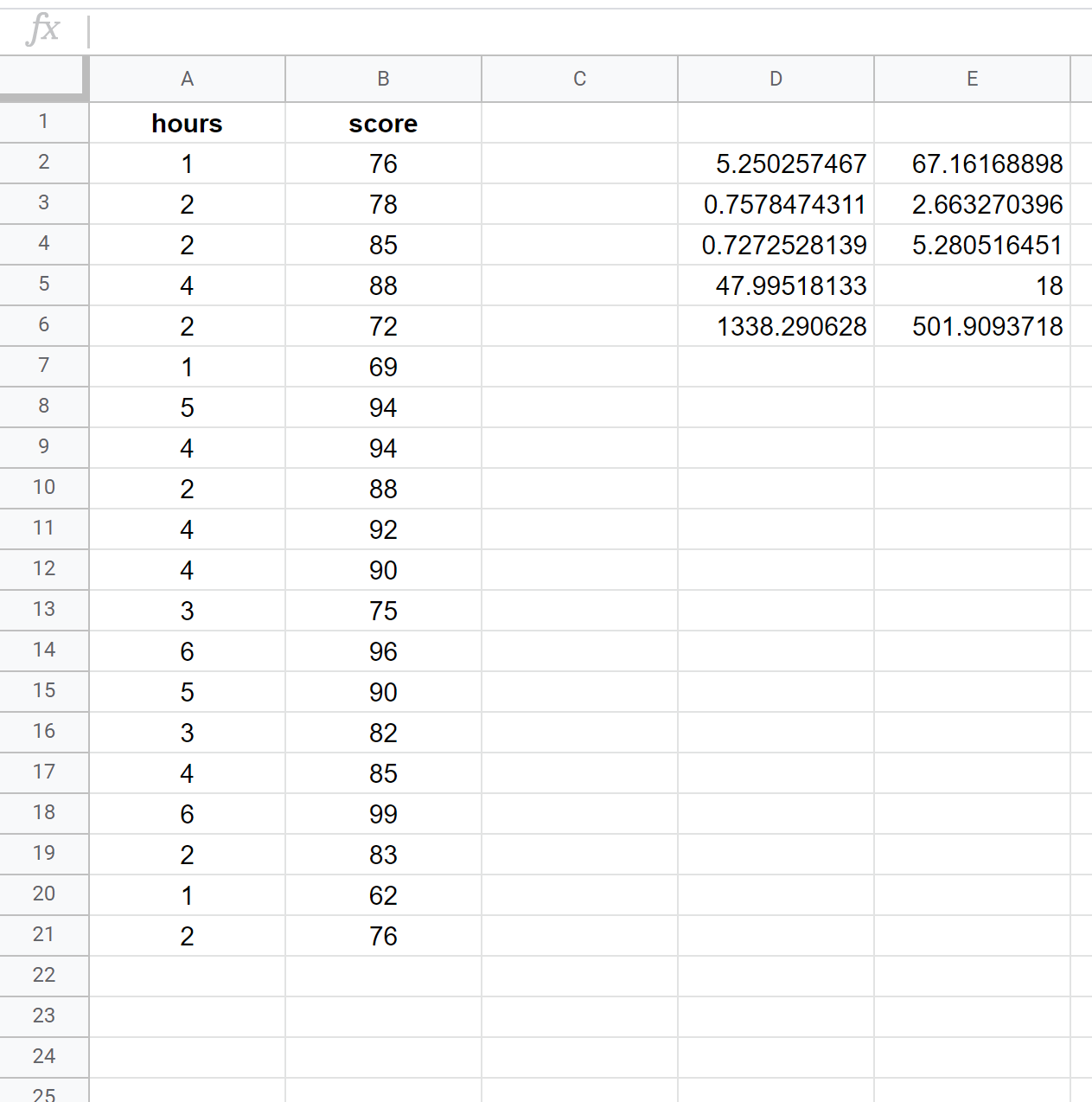
Lo screenshot seguente fornisce annotazioni per l’output:

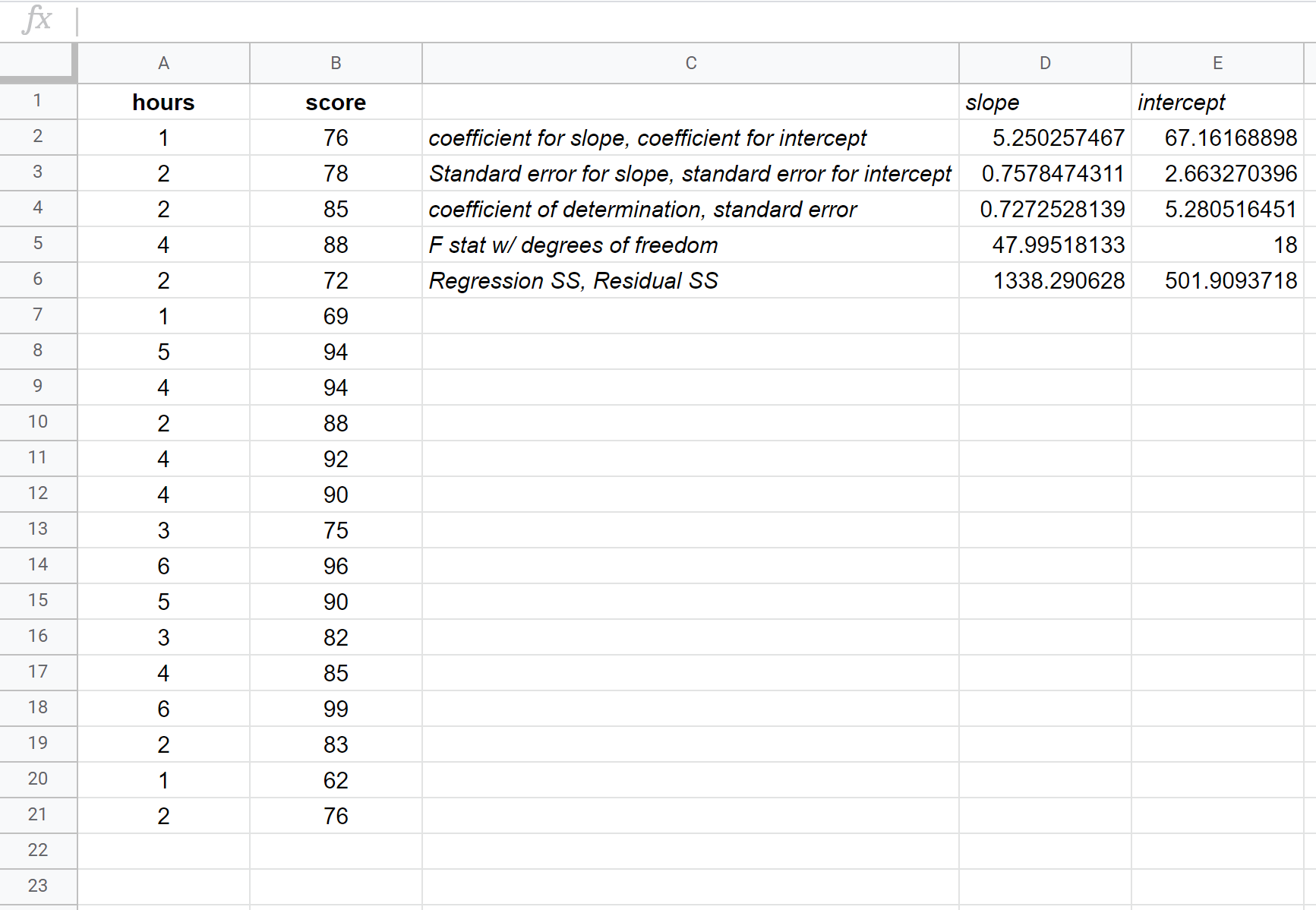
Ecco come interpretare i numeri più rilevanti nel risultato:

R quadrato: 0,72725 . Questo è chiamato coefficiente di determinazione. È la proporzione della varianza nella variabile di risposta che può essere spiegata dalla variabile esplicativa. In questo esempio, circa il 72,73% della variazione dei punteggi degli esami può essere spiegata dal numero di ore studiate.

Errore standard: 5.2805 . Questa è la distanza media tra i valori osservati e la retta di regressione. In questo esempio i valori osservati si discostano in media di 5.2805 unità dalla retta di regressione.

Coefficienti: i coefficienti ci forniscono i numeri necessari per scrivere l’equazione di regressione stimata. In questo esempio, l’equazione di regressione stimata è:

Punteggio esame = 67,16 + 5,2503*(ore)

Interpretiamo il coefficiente di ore nel senso che per ogni ora aggiuntiva studiata, il punteggio dell’esame dovrebbe aumentare in media di 5,2503 . Interpretiamo il coefficiente dell’intercetta nel senso che il punteggio atteso dell’esame per uno studente che studia zero ore è 67,16 .

Possiamo utilizzare questa equazione di regressione stimata per calcolare il punteggio atteso dell’esame per uno studente, in base al numero di ore di studio. Ad esempio, uno studente che studia per tre ore dovrebbe ottenere un punteggio d’esame di 82,91 :

Punteggio esame = 67,16 + 5,2503*(3) = 82,91

Regressione lineare multipla in Fogli Google

Supponiamo di voler sapere se il numero di ore trascorse a studiare e il numero di esami preparatori sostenuti influiscono sul voto che uno studente ottiene in un determinato esame di ammissione all’università.

Per esplorare questa relazione, possiamo eseguire una regressione lineare multipla utilizzando le ore studiate e gli esami preparatori presi come variabili esplicative e i risultati degli esami come variabile di risposta.

La schermata seguente mostra come eseguire una regressione lineare multipla utilizzando un set di dati di 20 studenti con la seguente formula utilizzata nella cella E2:

= DESTRA ( C2:C21 , A2:B21 , VERO , VERO )

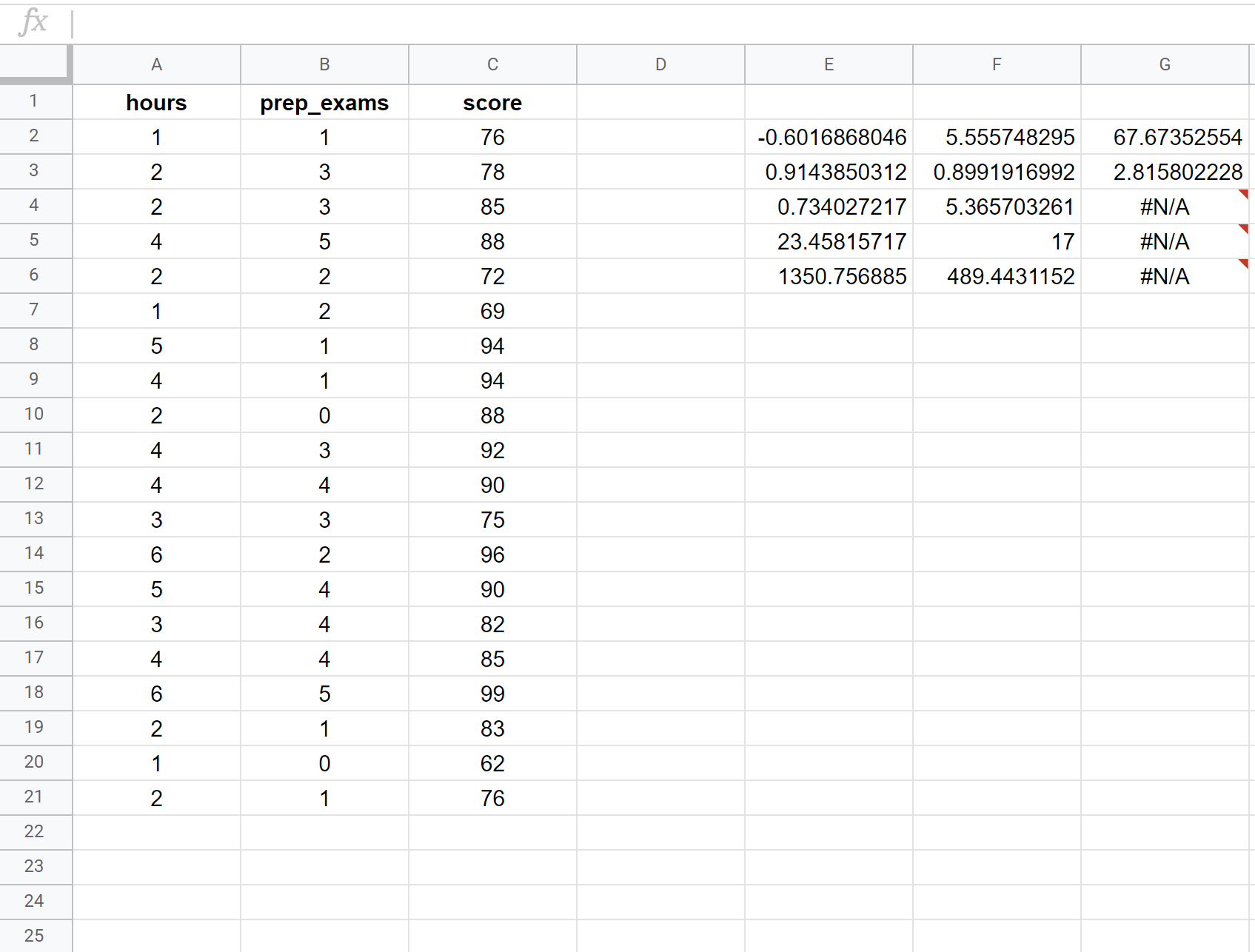
Ecco come interpretare i numeri più rilevanti nel risultato:

R quadrato: 0,734 . Questo è chiamato coefficiente di determinazione. È la proporzione della varianza della variabile di risposta che può essere spiegata dalle variabili esplicative. In questo esempio, il 73,4% della variazione dei punteggi degli esami è spiegata dal numero di ore studiate e dal numero di esami preparatori sostenuti.

Errore standard: 5.3657 . Questa è la distanza media tra i valori osservati e la retta di regressione. In questo esempio i valori osservati si discostano in media di 5.3657 unità dalla retta di regressione.

Equazione di regressione stimata: possiamo utilizzare i coefficienti dell’output del modello per creare la seguente equazione di regressione stimata:

Punteggio esame = 67,67 + 5,56*(ore) – 0,60*(esami preparatori)

Possiamo utilizzare questa equazione di regressione stimata per calcolare il punteggio atteso dell’esame per uno studente, in base al numero di ore di studio e al numero di esami pratici sostenuti. Ad esempio, uno studente che studia per tre ore e sostiene un esame di preparazione dovrebbe ottenere un voto di 83,75 :

Punteggio dell’esame = 67,67 + 5,56*(3) – 0,60*(1) = 83,75

Risorse addizionali

I seguenti tutorial spiegano come eseguire altre attività comuni in Fogli Google:

Come eseguire la regressione polinomiale in Fogli Google
Come creare una trama residua in Fogli Google