Comprendere la forma di una distribuzione binomiale

La distribuzione binomiale descrive la probabilità di ottenere k successi in n esperimenti binomiali.

Se una variabile casuale X segue una distribuzione binomiale, la probabilità che X = k successo può essere trovata con la seguente formula:

P(X=k) = _n C _k * p ^k * (1-p) ^nk

Oro:

• n: numero di prove
• k: numero di successi
• p: probabilità di successo in una determinata prova
• _n C _k : il numero di modi per ottenere k successi in n prove

La distribuzione di probabilità binomiale tende ad essere a campana quando si verifica una o più delle seguenti due condizioni:

1. La dimensione del campione (n) è ampia.

2. La probabilità di successo per una determinata prova (p) è vicina a 0,5.

Tuttavia, la distribuzione di probabilità binomiale tende ad essere distorta quando non si verifica nessuna di queste condizioni. Per illustrare ciò, si considerino i seguenti esempi:

Esempio 1: la dimensione del campione (n) è ampia

Il grafico seguente mostra la distribuzione di probabilità quando n = 200 e p = 0,5 .

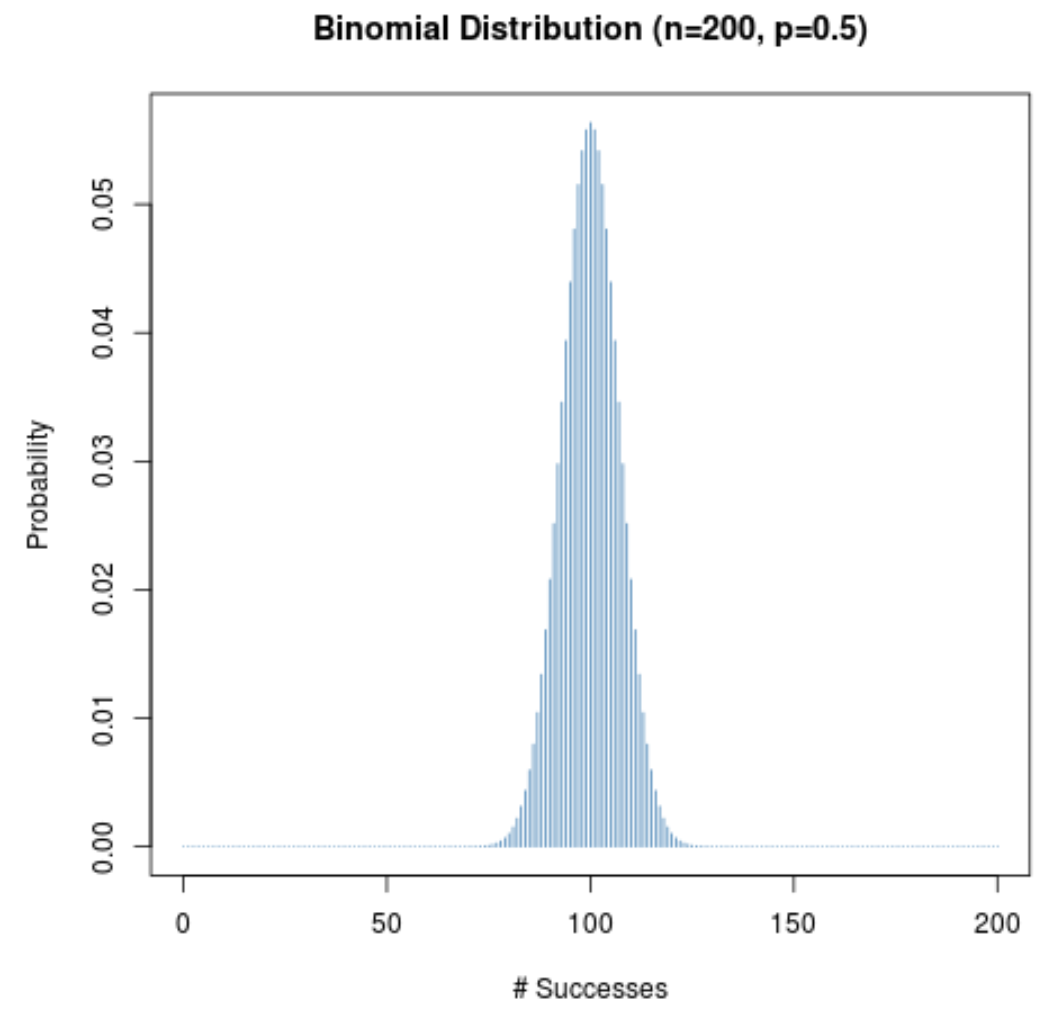
L’asse x mostra il numero di successi su 200 prove e l’asse y mostra la probabilità che si verifichi quel numero di successi.

Poiché (1) la dimensione del campione è ampia e (2) la probabilità di successo per un dato esperimento è vicina a 0,5, la distribuzione di probabilità è a campana.

Anche quando la probabilità di successo per una data prova (p) non è vicina a 0,5, la distribuzione di probabilità rimarrà a campana finché la dimensione del campione (n) è ampia. Per illustrare ciò, si considerino i due scenari seguenti quando p = 0,2 e p = 0,8.

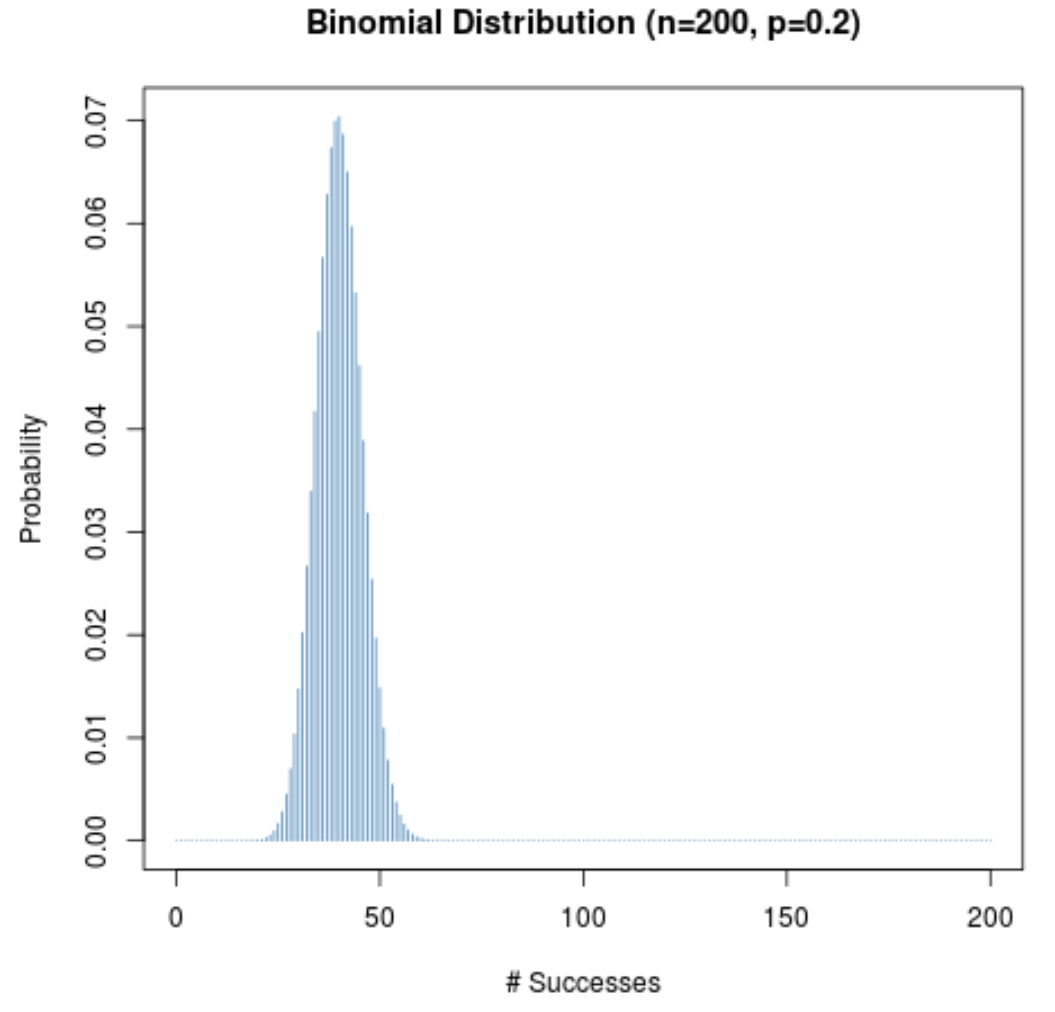
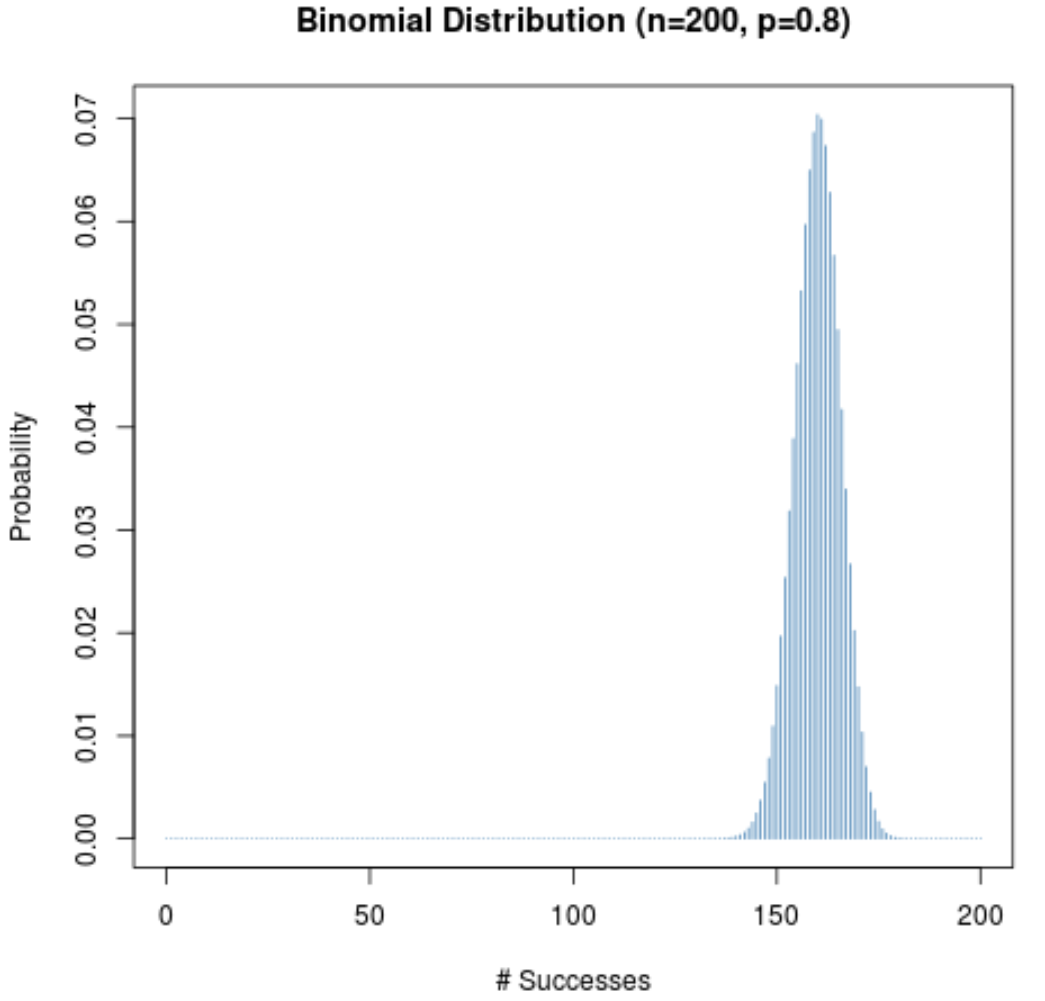
Si noti come la distribuzione di probabilità è a campana in entrambi gli scenari.

Esempio 2: la probabilità di successo (p) è vicina a 0,5

Il grafico seguente mostra la distribuzione di probabilità quando n = 10 e p = 0,4 .

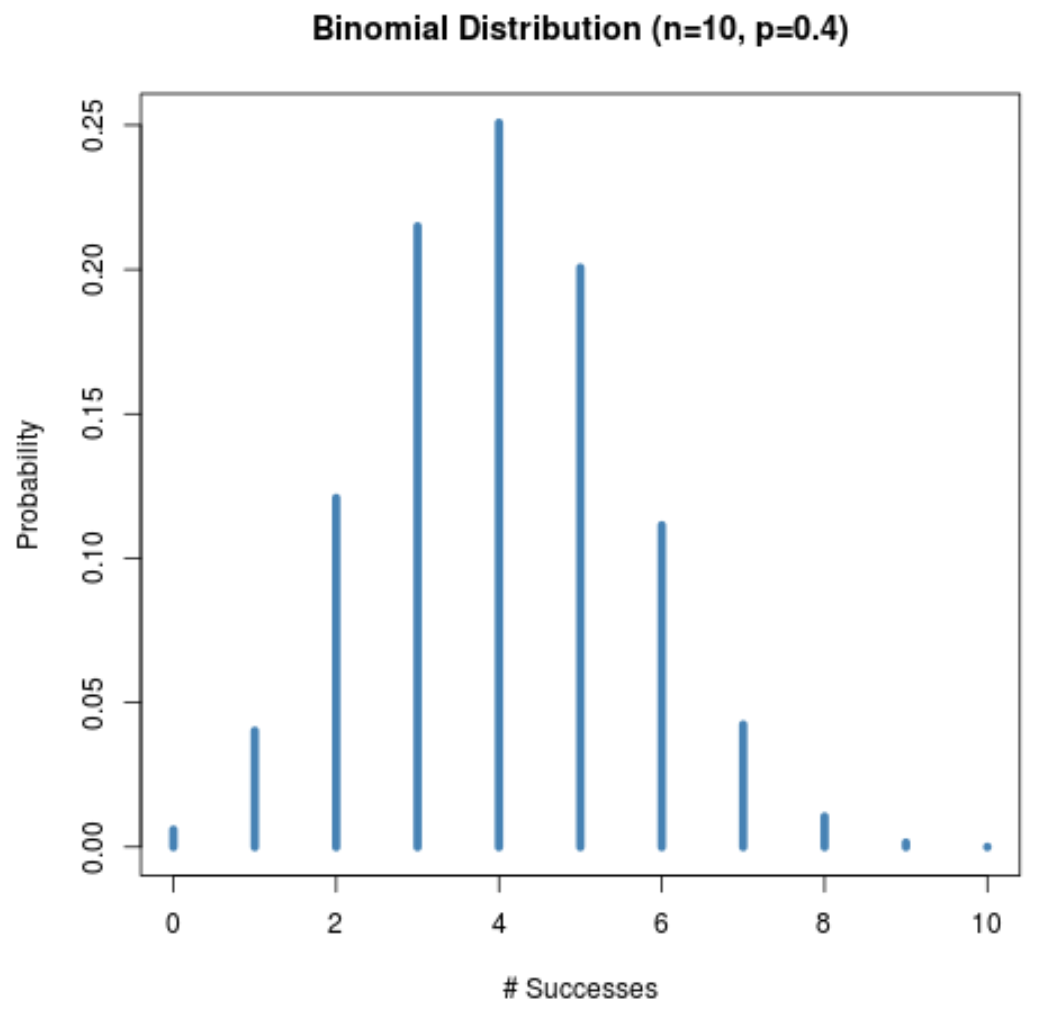
Sebbene la dimensione del campione (n = 10) sia piccola, la distribuzione di probabilità rimane a campana perché la probabilità di successo per un dato studio (p = 0,4) è vicina a 0,5.

Esempio 3: distribuzioni binomiali distorte

Quando né (1) la dimensione del campione è ampia né (2) la probabilità di successo di un dato esperimento è vicina a 0,5, la distribuzione binomiale della probabilità sarà sbilanciata a sinistra o a destra.

Ad esempio, il grafico seguente mostra la distribuzione di probabilità quando n = 20 e p = 0,1 .

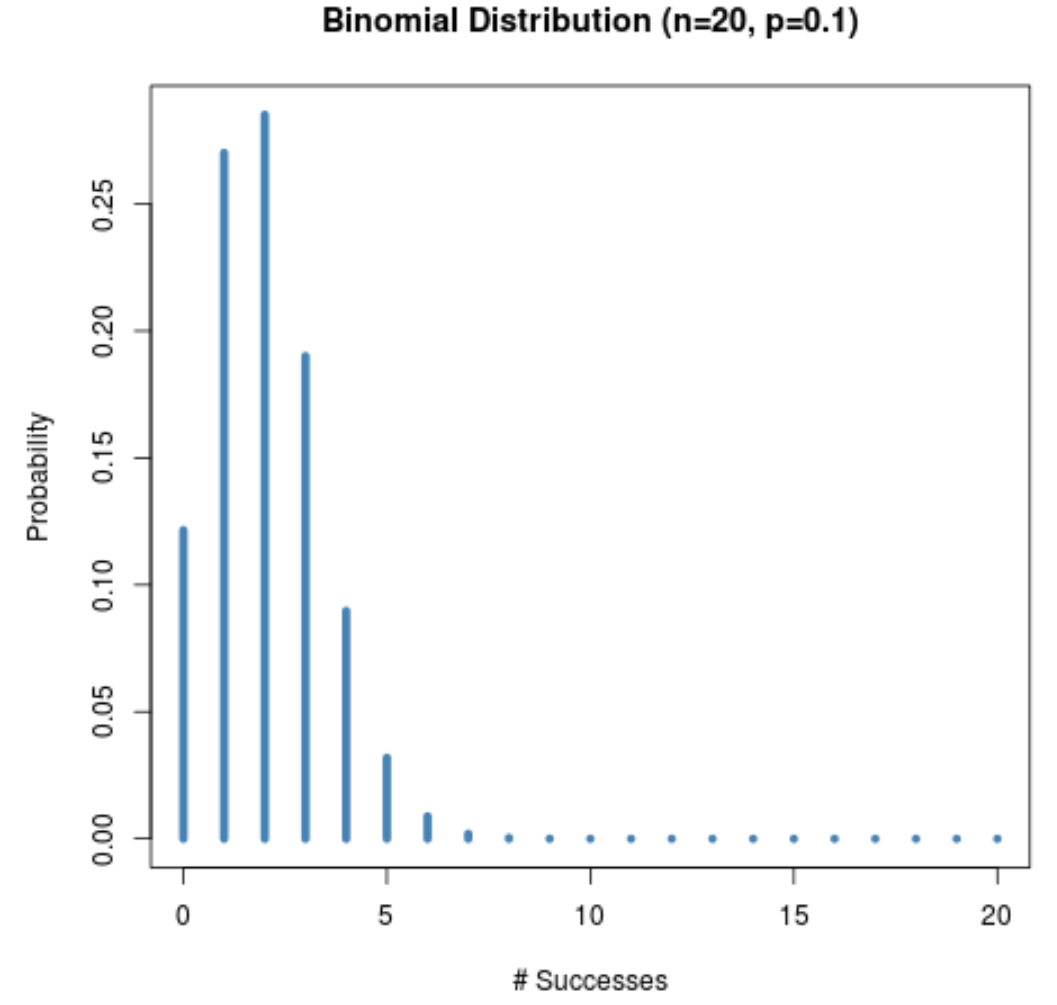
Notare come la distribuzione è inclinata a destra.

E il grafico seguente mostra la distribuzione di probabilità quando n = 20 e p = 0,9 .

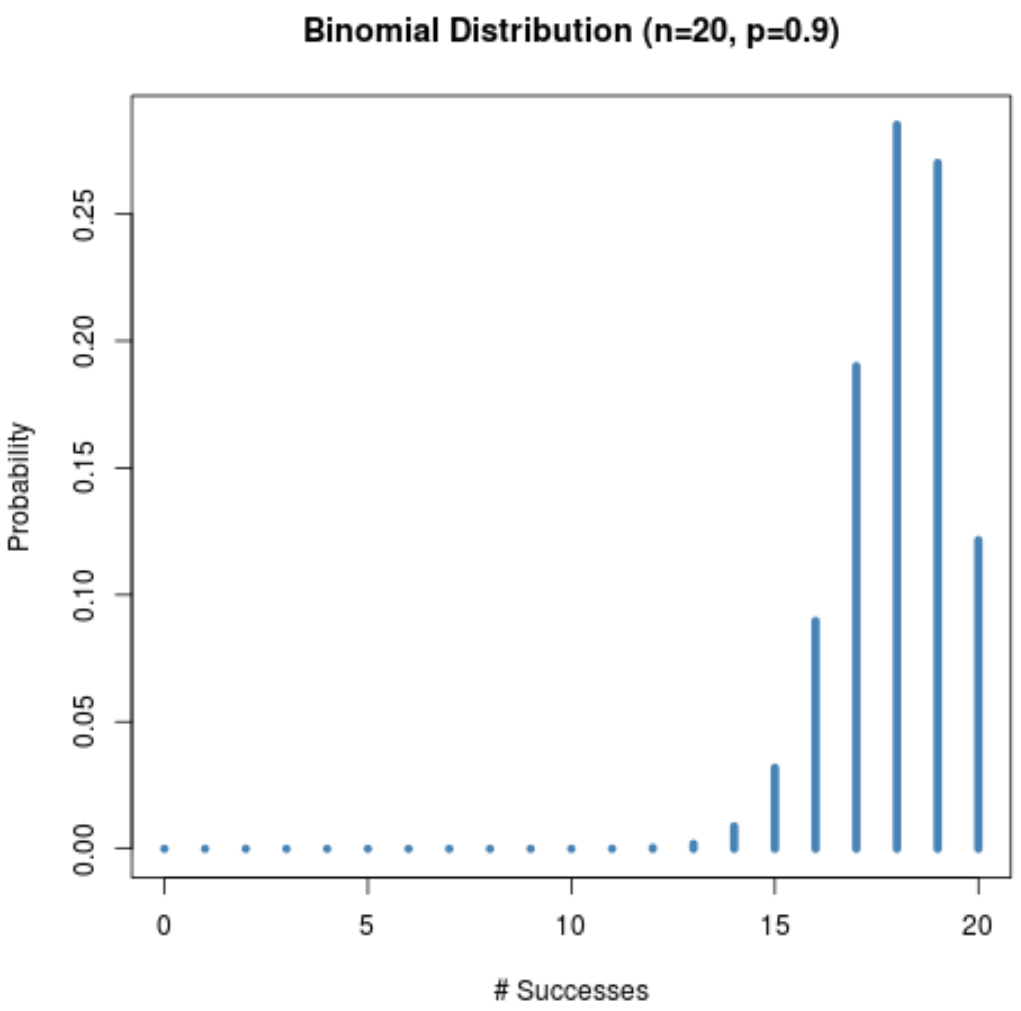
Notare come la distribuzione è sbilanciata a sinistra.

Note finali

Ciascuno dei grafici in questo articolo è stato creato utilizzando il linguaggio di programmazione statistica R. Scopri come tracciare le tue distribuzioni di probabilità binomiali in R utilizzando questo tutorial .