Frequenza assoluta

Questo articolo spiega il significato della frequenza assoluta nelle statistiche. Scoprirai così come ottenere la frequenza assoluta di un set di dati, due esercizi risolti e, inoltre, le differenze con altri tipi di frequenze statistiche.

Qual è la frequenza assoluta?

Nelle statistiche, la frequenza assoluta è il numero di volte in cui un valore appare in un set di dati. In poche parole, la frequenza assoluta è il numero di volte in cui un risultato viene ripetuto.

Ad esempio, se sette persone in un sondaggio rispondono che il loro colore preferito è il rosso, la frequenza assoluta del colore rosso è 7.

Pertanto, la somma delle frequenze assolute di tutti i valori è uguale al numero totale di dati nel campione statistico.

In generale, la lettera f con pedice i viene utilizzata per rappresentare la frequenza assoluta del valore i , quindi il simbolo per la frequenza assoluta è _fi .

Come calcolare la frequenza assoluta

Per ottenere le frequenze assolute di un set di dati, è necessario seguire i seguenti passaggi:

1. Se la variabile è discreta, crea un array di tutti i diversi valori che compaiono nel set di dati, ovvero posiziona ogni valore diverso in una riga di una tabella.
2. Se la variabile è continua, raggruppa i dati in intervalli e crea una tabella con tutti gli intervalli.
3. Contare il numero di volte in cui un valore appare nel set di dati e registrare il risultato nella tabella delle frequenze.
4. Ripetere il passaggio precedente per ogni valore diverso nei dati di esempio.

Esempi di frequenza assoluta

Dopo aver visto la definizione di frequenza assoluta e la teoria su come si calcola, vedremo due esempi per farti capire come si fa. Nel primo esempio determineremo le frequenze assolute di una variabile discreta e nel secondo esempio di una variabile continua, poiché la procedura varia leggermente a seconda dei casi.

Esempio 1: variabile discreta

• I voti ottenuti in statistica in una classe di 30 studenti sono i seguenti. Qual è la frequenza assoluta di ciascuna nota?

In questo caso si tratta di una variabile discreta perché possono esserci solo numeri interi, quindi non è necessario raggrupparli in intervalli.

Quindi basta contare le volte in cui appare ciascun valore e scriverlo in una tabella di frequenza:

Si noti che la somma di tutte le frequenze assolute è uguale al numero totale di punti dati. Se questa regola non viene seguita significa che hai dimenticato di contare alcuni dati.

Esempio 2: variabile continua

• È stata misurata l’altezza di 20 persone e sono stati ottenuti i risultati riportati di seguito. Separa i dati in intervalli e trova la frequenza assoluta di ciascun intervallo.

I dati in questo esempio seguono una distribuzione continua, poiché i numeri possono essere decimali. Dobbiamo quindi raggruppare i dati in intervalli, in questo caso realizzeremo intervalli con una larghezza di 10 decimi.

Quindi, contiamo il numero di dati in ciascun intervallo e rappresentiamo le frequenze assolute in una tabella:

Frequenza assoluta e frequenza assoluta cumulativa

Come suggerisce il nome, la frequenza assoluta cumulativa è un altro tipo di frequenza utilizzata nelle statistiche e correlata alla frequenza assoluta.

La frequenza assoluta cumulativa di un valore è pari alla somma della frequenza assoluta del valore stesso più le frequenze assolute di tutti i valori precedenti.

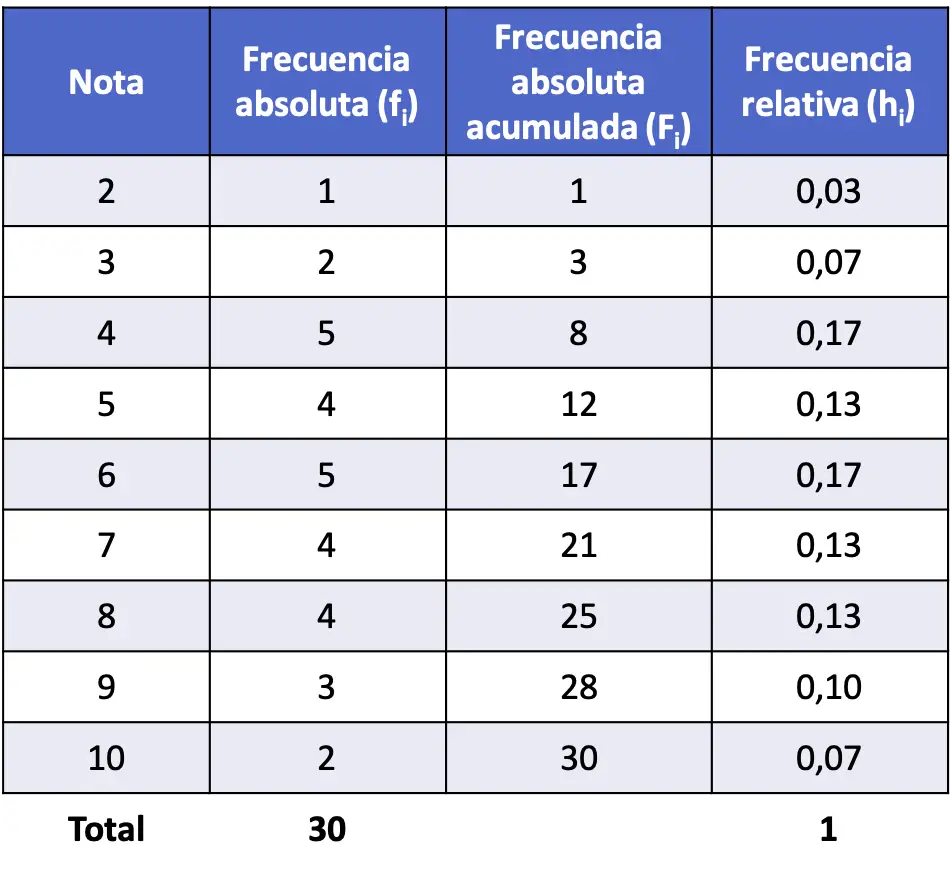
A titolo di esempio potete vedere qui sotto il calcolo delle frequenze assolute accumulate del primo esercizio risolto sopra:

Frequenza assoluta e frequenza relativa

In statistica la frequenza relativa è un tipo di frequenza diversa dalle due viste sopra, poiché rappresenta la percentuale di ciascun valore rispetto al totale. Ecco perché in questa sezione vedremo la differenza tra questi due concetti.

La differenza tra frequenza assoluta e frequenza relativa è che la frequenza assoluta è il numero assoluto di valori in un campione, mentre la frequenza relativa è la proporzione di ciascun valore rispetto al totale.

Pertanto, la frequenza relativa viene calcolata dividendo la frequenza assoluta per il numero totale di dati.