Frequenza cumulativa

Questo articolo spiega qual è la frequenza cumulativa nelle statistiche. Quindi imparerai il significato della frequenza cumulativa, come viene calcolata la frequenza cumulativa con esempi e, infine, i diversi tipi di frequenze cumulative che esistono.

Qual è la frequenza cumulativa?

Nelle statistiche, la frequenza cumulativa è la somma cumulativa delle frequenze. Cioè, la frequenza cumulativa di un valore è uguale alla frequenza di quel valore più le frequenze di tutti i valori inferiori.

Esistono due tipi di frequenze cumulative: frequenza assoluta cumulativa e frequenza relativa cumulativa. Di seguito vedremo come viene calcolata ciascuna tipologia di frequenza cumulativa.

Tieni presente che per capire cosa significa frequenza cumulativa nelle statistiche, devi prima avere chiaro il concetto di frequenza. Questo è il motivo per cui si consiglia di visitare il seguente post prima di continuare con la spiegazione:

Come calcolare la frequenza cumulativa

I passaggi per calcolare la frequenza cumulativa di un campione statistico sono:

1. Crea una tabella con tutti i diversi valori che compaiono nel set di dati, ordinati dal più piccolo al più grande.
2. Trova la frequenza assoluta di ciascun valore.
3. Trova la frequenza cumulativa di ciascun valore, che viene calcolata sommando la frequenza del valore stesso più le frequenze di tutti i valori più piccoli.

Pertanto, la formula per il calcolo della frequenza cumulativa è:

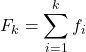
Oro:

• 

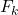
  è la frequenza cumulativa del valore

  

  .

• 

  è la frequenza assoluta del valore

  

  .

Tieni presente che questi passaggi servono per calcolare la frequenza assoluta cumulativa, ma esiste anche una frequenza relativa cumulativa. Di seguito vedremo la differenza tra questi due tipi di frequenze accumulate e come si trova ciascun tipo.

Tipi di frequenze cumulative

Nelle statistiche, ci sono due tipi di frequenze cumulative :

• Frequenza assoluta cumulativa : è la somma cumulativa delle frequenze assolute .
• Frequenza relativa cumulativa : è la somma cumulativa delle frequenze relative .

Considerando la definizione di ciascun tipo di frequenza accumulata, puoi vedere di seguito un esempio di come ciascuna viene ottenuta.

Frequenza assoluta cumulativa

La frequenza assoluta cumulativa è rappresentata dal simbolo F _i e si calcola sommando le frequenze assolute di valori uguali o inferiori al valore in questione. Successivamente, hai un esempio concreto in cui viene calcolata la frequenza assoluta cumulativa di un set di dati statistici.

• I voti ottenuti in materia di statistica in una classe di 30 studenti sono i seguenti. Qual è la frequenza assoluta cumulativa di ciascuna nota?

Poiché tutti i numeri possono essere solo numeri interi, è una variabile discreta. Non è quindi necessario raggruppare i dati in intervalli.

Quindi, per determinare la frequenza assoluta cumulativa, dobbiamo prima trovare la frequenza assoluta di ciascun valore, ovvero il numero di volte in cui ciascun valore appare nel campione statistico.

Ora che conosciamo la frequenza assoluta di ciascun valore, possiamo calcolare le loro frequenze assolute cumulative. Per fare ciò, abbiamo due opzioni: o aggiungiamo la frequenza assoluta del valore più tutte le frequenze assolute dei valori più piccoli, oppure, al contrario, aggiungiamo la frequenza assoluta del valore più la frequenza assoluta cumulativa dei valori precedenti . valore.

In breve, la tabella con la frequenza cumulativa assoluta dell’esercizio è la seguente:

Si noti che la frequenza assoluta accumulata dell’ultimo valore coincide sempre con il numero totale di dati. Altrimenti significa che hai commesso un errore nel calcolo.

Frequenza relativa cumulativa

La frequenza relativa cumulativa è rappresentata dal simbolo H _i e si calcola sommando le frequenze relative di valori uguali o inferiori al valore in questione. Di seguito puoi vedere un esercizio risolto con gli stessi dati del problema precedente in cui viene determinata la frequenza relativa cumulativa.

• I voti ottenuti in statistica in una classe di 30 studenti sono i seguenti. Qual è la frequenza relativa cumulativa di ciascuna nota?

In questo caso la variabile è discreta poiché non può assumere un valore decimale. Quindi non è necessario raggruppare i dati per intervalli, ma possiamo fare direttamente i calcoli.

Quindi, redigiamo una tabella di frequenza e determiniamo la frequenza assoluta di ogni diverso valore:

Successivamente, calcoliamo la frequenza relativa di ciascun valore, che viene determinata dividendo la frequenza assoluta per il numero totale di osservazioni (30).

E una volta calcolata la frequenza assoluta e relativa del set di dati, possiamo ottenere la frequenza relativa cumulativa. Per fare ciò, è necessario aggiungere la frequenza relativa del valore in questione più tutte le frequenze relative precedenti o, che è la stessa cosa, la frequenza relativa accumulata precedente:

In breve, la tabella delle frequenze con frequenza assoluta, frequenza relativa e frequenza relativa cumulativa è la seguente:

Tieni presente che l’ultimo valore della frequenza relativa cumulativa dovrebbe essere sempre 1. Se ottieni un altro numero, significa che hai commesso un errore nei calcoli.