Frequenza relativa

In questo articolo imparerai cos’è la frequenza relativa nelle statistiche, come ottenere la frequenza relativa e due esercizi passo passo risolti sulla frequenza relativa.

Qual è la frequenza relativa?

Nelle statistiche, la frequenza relativa è una misura che indica il numero di volte in cui un valore appare in un campione di dati come proporzione o percentuale. Più precisamente, la frequenza relativa è uguale alla frequenza assoluta divisa per il numero totale di dati.

Ad esempio, se la frequenza assoluta di un valore è 15 e sono presenti 100 punti dati in totale, la frequenza relativa di tale valore è 0,15 (15/100=0,15).

Generalmente, il simbolo h _i viene utilizzato per rappresentare la frequenza relativa. Sebbene non vi sia ancora consenso nella comunità statistica, è possibile vedere la frequenza relativa rappresentata da un altro simbolo.

Come calcolare la frequenza relativa

La frequenza relativa è uguale alla frequenza assoluta divisa per il numero totale di dati. Pertanto, per calcolare la frequenza relativa, è necessario prima trovare la frequenza assoluta e poi dividerla per il numero totale di osservazioni.

Quindi, la formula per la frequenza relativa è la seguente:

Oro:

• 

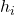
  è la frequenza relativa.

• 

  è la frequenza assoluta.

• 

  è il numero totale di dati.

Per calcolare invece la frequenza relativa in percentuale , cioè la frequenza relativa espressa in percentuale, è sufficiente moltiplicare la formula precedente per 100:

Esempi di frequenza relativa

Dopo aver visto la definizione di frequenza relativa, di seguito sono riportati due esempi reali in modo da poter vedere come viene calcolato questo tipo di frequenza. Nel primo esempio viene determinata la frequenza relativa di una variabile discreta e nel secondo esempio una variabile continua.

Esempio 1: variabile discreta

• I voti ottenuti in materia di statistica in una classe di 30 studenti sono i seguenti. Qual è la frequenza relativa di ciascuna nota?

La variabile in questo esercizio è discreta perché i dati possono essere solo numeri interi; pertanto non è necessario raggruppare i dati in intervalli.

Per trovare la frequenza relativa, dobbiamo prima determinare la frequenza assoluta. Quindi costruiamo una tabella di frequenza e calcoliamo la frequenza assoluta per ogni diverso valore:

Ora che abbiamo calcolato la frequenza assoluta, possiamo calcolare la frequenza relativa. Per fare ciò, dividi semplicemente ciascuna frequenza assoluta per il numero totale di dati (30):

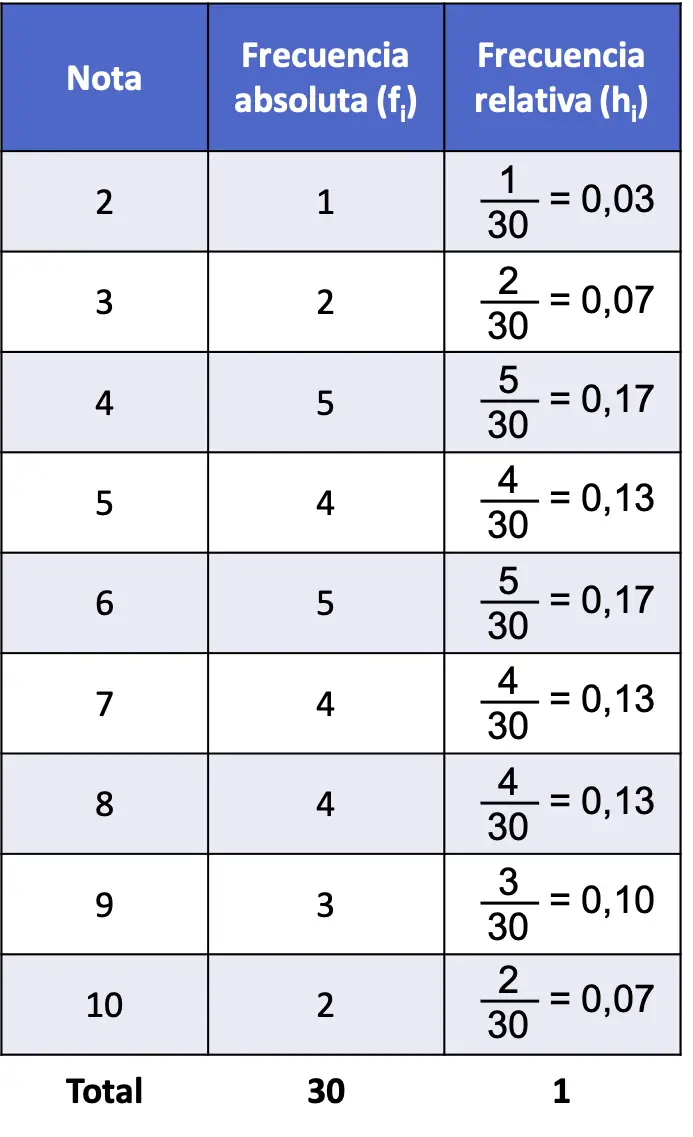
Quindi, la tabella delle frequenze del problema con frequenza assoluta e frequenza relativa è la seguente:

Si noti che la somma di tutte le frequenze relative dà sempre 1, altrimenti significa che alcuni calcoli sono sbagliati.

Esempio 2: variabile continua

• È stata misurata l’altezza di 20 persone e sono stati ottenuti i risultati riportati di seguito. Separa i dati in intervalli e trova la frequenza relativa di ciascun intervallo.

I dati di questo campione statistico appartengono ad una variabile continua, poiché sono decimali e quindi la variabile può assumere qualsiasi valore. Quindi prima di fare i calcoli della frequenza, raggrupperemo prima i dati in intervalli con un’ampiezza di 10 decimi.

Successivamente, creiamo una tabella di frequenza con la frequenza assoluta di ciascun intervallo:

E una volta trovata la frequenza assoluta, possiamo ottenere la frequenza relativa di ciascun intervallo dividendo la sua frequenza assoluta per il numero totale di dati (20):

Frequenza relativa cumulativa

Come suggerisce il nome, la frequenza relativa cumulativa è un altro tipo di frequenza utilizzata nelle statistiche e calcolata dalla frequenza relativa.

Più precisamente, la frequenza relativa cumulativa di un valore è pari alla somma della frequenza relativa del valore stesso più le frequenze relative di tutti i valori più piccoli.

Per poter vedere come viene ottenuta la frequenza relativa cumulativa, la frequenza relativa cumulativa del set di dati nel primo esempio è stata calcolata di seguito: