Frequenza relativa cumulativa

Questo articolo spiega quale sia la frequenza relativa cumulativa nelle statistiche. Quindi troverai la definizione di frequenza relativa cumulativa, come ottenere la frequenza relativa cumulativa e due esercizi risolti passo dopo passo.

Qual è la frequenza relativa cumulativa?

Nelle statistiche, la frequenza relativa cumulativa è la somma cumulativa delle frequenze relative. Cioè, la frequenza relativa cumulativa di un valore è uguale alla frequenza relativa di quel valore più le frequenze relative di tutti i valori inferiori ad esso.

Il simbolo per la frequenza relativa cumulativa è H _i . Tuttavia, nelle statistiche non esiste ancora un consenso completo riguardo al simbolo di questo tipo di frequenza, motivo per cui potresti trovarlo espresso anche con un altro simbolo.

Ovviamente, per comprendere il significato di frequenza relativa cumulativa, devi prima avere chiaro il concetto di frequenza relativa, motivo per cui ti consiglio di visitare il seguente link prima di proseguire con la spiegazione:

Come calcolare la frequenza relativa cumulativa

Per calcolare la frequenza relativa cumulativa, è necessario seguire i seguenti passaggi:

1. Costruisci una tabella di frequenza con tutti i diversi valori del campione statistico.
2. Calcolare la frequenza assoluta di ciascun valore.
3. Dalle frequenze assolute, determinare la frequenza relativa di ciascun valore.
4. Trova la frequenza relativa cumulativa di ciascun valore, che viene calcolata sommando la frequenza relativa del valore stesso più le frequenze relative di tutti i valori più piccoli.

Tieni presente che se desideri calcolare la percentuale di frequenza relativa cumulativa , ovvero la frequenza relativa cumulativa espressa in percentuale, devi solo seguire gli stessi passaggi e moltiplicare i risultati per 100.

Esempi di frequenza relativa cumulativa

Per farti vedere come viene calcolata la frequenza relativa cumulativa, di seguito vengono mostrati due esempi risolti passo dopo passo. Nel primo esempio troviamo la frequenza relativa cumulativa di una variabile discreta e nel secondo esempio una variabile continua, poiché il processo varia leggermente.

Esempio 1: variabile discreta

• I voti ottenuti in materia di statistica in una classe di 30 studenti sono i seguenti. Qual è la frequenza relativa cumulativa di ciascuna nota?

In questo caso la variabile è discreta poiché non può assumere un valore decimale. Non è quindi necessario raggruppare i dati per intervalli, ma i calcoli possono essere fatti direttamente.

Quindi, redigiamo una tabella di frequenza e determiniamo la frequenza assoluta di ogni diverso valore:

Successivamente, calcoliamo la frequenza relativa di ciascun valore (puoi vedere come farlo nel link all’inizio del post).

E una volta calcolata la frequenza assoluta e relativa del set di dati, possiamo ottenere la frequenza relativa cumulativa. Per fare ciò, dobbiamo aggiungere la frequenza relativa del valore in questione più tutte le frequenze relative precedenti o, in altre parole, la frequenza relativa accumulata precedente:

In breve, la tabella delle frequenze con frequenza assoluta, frequenza relativa e frequenza relativa cumulativa è la seguente:

Tieni presente che l’ultimo valore della frequenza relativa cumulativa dovrebbe essere sempre 1. Se ottieni un altro numero, significa che hai commesso un errore nei calcoli.

Esempio 2: variabile continua

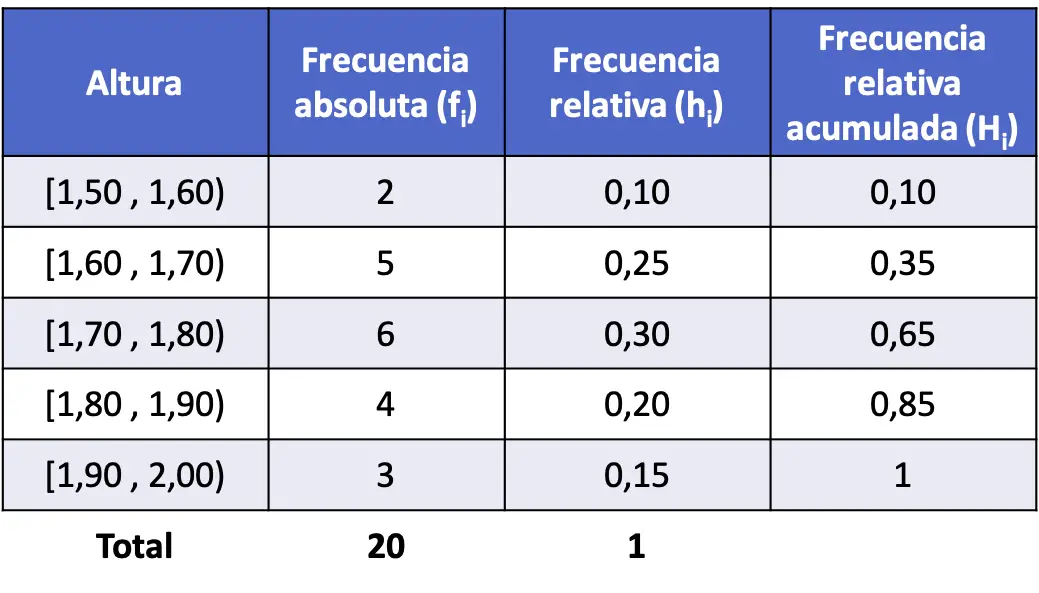
• È stata misurata l’altezza di 20 persone e sono stati ottenuti i risultati riportati di seguito. Separa i dati in intervalli e trova la frequenza relativa cumulativa di ciascun intervallo.

Questo caso è diverso dal problema precedente poiché i numeri sono decimali, il che significa che la variabile può assumere qualsiasi valore ed è quindi continua. Creeremo quindi la tabella delle frequenze raggruppando i dati in intervalli.

Costruiamo quindi la tabella e otteniamo la frequenza assoluta di ciascun intervallo:

Ora calcoliamo le frequenze relative dividendo la frequenza assoluta di ciascun intervallo per il numero totale di punti dati:

E infine, troviamo le frequenze relative cumulative di tutti gli intervalli. Come prima, per determinare una frequenza relativa cumulativa di un intervallo è necessario sommare la frequenza relativa di detto intervallo più le frequenze relative precedenti:

Frequenza relativa cumulativa e frequenza assoluta cumulativa

Abbiamo appena visto come la frequenza relativa cumulativa derivi dalla frequenza relativa. Tuttavia, questo tipo di frequenza può essere trovato anche utilizzando la frequenza assoluta cumulativa.

La frequenza relativa cumulativa può essere calcolata dividendo la frequenza assoluta cumulativa per il numero totale di dati nel campione.

Pertanto, la formula per la frequenza relativa cumulativa è:

Oro:

• 

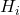
  è la frequenza relativa cumulativa.

• 

  è la frequenza assoluta accumulata .

• 

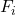
  è il numero totale di dati.

Seguendo il primo esempio sviluppato sopra, ecco come si ricava la frequenza relativa accumulata dalla frequenza assoluta accumulata:

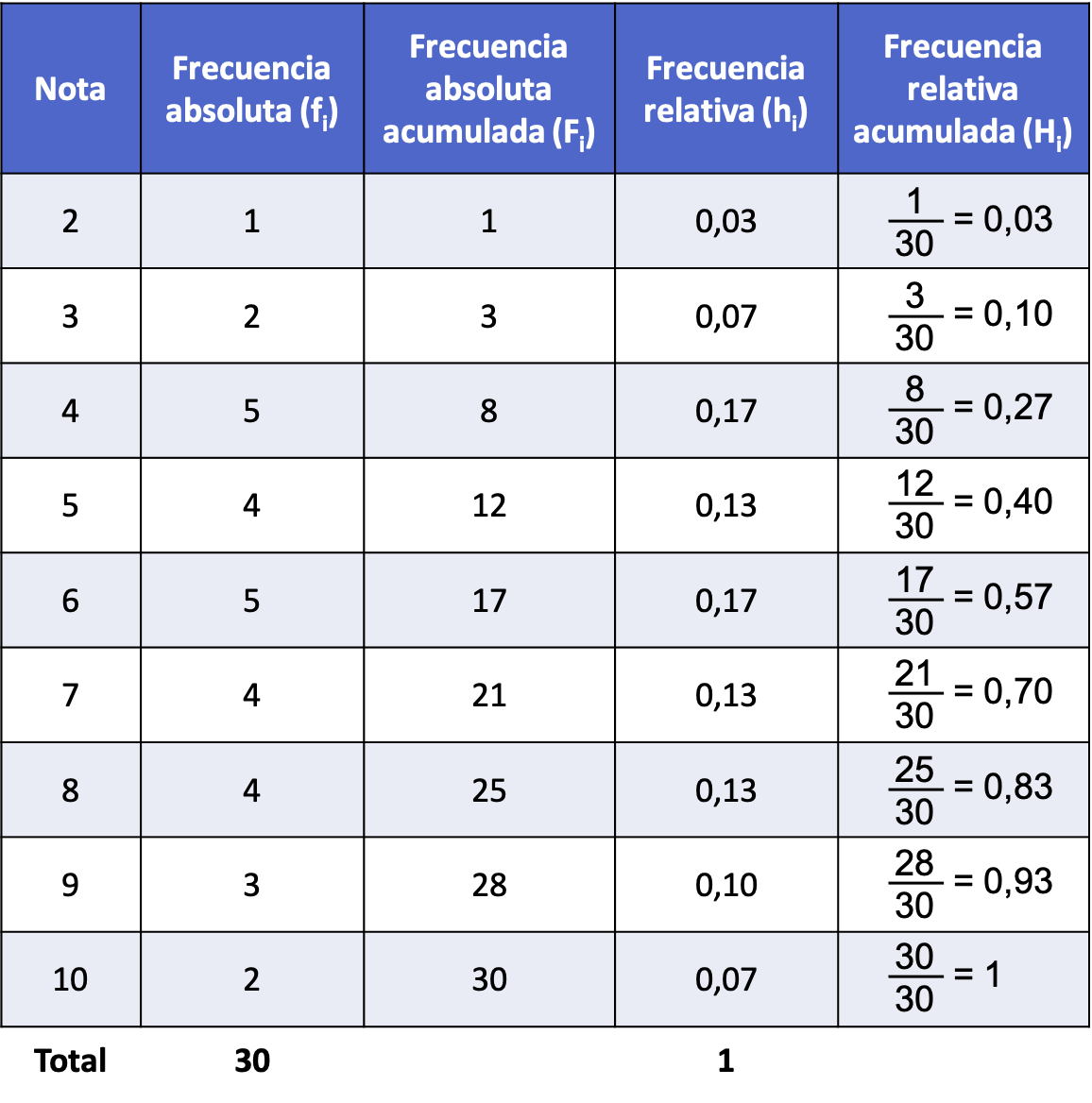
La tabella precedente, poiché contiene tutti i tipi di frequenze statistiche, è chiamata tabella delle frequenze. Clicca qui per saperne di più: