Frequenza (statistica)

Questo articolo spiega qual è la nozione di frequenza nelle statistiche. Troverai quindi la definizione di frequenza in statistica, i diversi tipi di frequenze esistenti e, infine, come creare una tabella di frequenza.

Qual è la frequenza nelle statistiche?

Nelle statistiche, la frequenza è il numero di volte in cui un valore appare in un set di dati. In poche parole, la frequenza è il numero di volte in cui un valore viene ripetuto in un campione statistico.

Ad esempio, se in un sondaggio cinque persone rispondono che il loro colore preferito è il blu, allora la frequenza del colore blu è pari a 5.

Generalmente, in statistica, la lettera f con indice i viene utilizzata per rappresentare la frequenza del valore i , quindi il simbolo della frequenza è _fi .

La somma di tutte le frequenze fornisce il numero totale di dati nel campione. Pertanto, per qualsiasi studio statistico vale sempre la seguente formula:

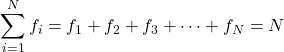
Oro

è la frequenza del valore

E

è il numero totale di osservazioni.

Tipi di frequenze in statistica

In statistica, i diversi tipi di frequenze sono i seguenti:

• Frequenza assoluta : corrisponde al numero di volte in cui un valore appare in un campione statistico.
• Frequenza assoluta cumulativa : calcolata sommando la frequenza assoluta del valore più le frequenze assolute di tutti i valori più piccoli.
• Frequenza relativa : è la frequenza assoluta divisa per il numero totale di dati.
• Frequenza relativa cumulativa : equivale alla somma della frequenza relativa del valore più le frequenze relative di tutti i valori inferiori.

Nella sezione seguente puoi vedere come viene calcolato ciascun tipo di frequenza.

Tabella delle frequenze

Tipicamente nelle statistiche, i calcoli delle frequenze di un campione di dati sono riepilogati in una tabella di frequenza. Di seguito è riportato un esempio passo passo in modo da poter vedere come farlo.

• I voti ottenuti in materia di statistica in una classe di 30 studenti sono i seguenti. Costruire una tabella di frequenza del set di dati.

Poiché tutti i numeri possono essere solo numeri interi, è una variabile discreta. Non è quindi necessario raggruppare i dati in intervalli.

Quindi dobbiamo costruire una tabella in cui ogni valore diverso sarà una riga. Inoltre, dobbiamo trovare la frequenza assoluta di ciascun valore, per fare ciò contiamo semplicemente il numero di volte in cui il valore appare nel campione di dati.

Si noti che la somma di tutte le frequenze assolute è uguale al numero totale di dati. Se questa regola non viene rispettata significa che hai dimenticato di fornire alcuni dati.

Ora che conosciamo la frequenza assoluta, dobbiamo trovare la frequenza assoluta cumulativa. Per questo calcolo abbiamo due opzioni: o aggiungiamo la frequenza assoluta del valore più tutte le frequenze assolute dei valori più piccoli, oppure, al contrario, aggiungiamo la frequenza assoluta del valore più la frequenza assoluta cumulativa del valore precedente.

La frequenza assoluta cumulativa dell’ultimo valore corrisponde sempre al numero totale di dati, puoi utilizzare questo trucco per verificare che i calcoli siano corretti.

Successivamente, dobbiamo determinare la frequenza relativa, che viene calcolata dividendo la frequenza assoluta per il numero totale di punti dati (30):

Tieni presente che la somma di tutte le frequenze relative è sempre uguale a 1, altrimenti significa che alcuni calcoli nella tabella delle frequenze sono errati.

Infine è sufficiente estrarre la frequenza relativa accumulata. Per fare ciò, è necessario aggiungere la frequenza relativa del valore in questione più tutte le frequenze relative precedenti o, che è la stessa cosa, la frequenza relativa accumulata precedente:

In breve, la tabella delle frequenze con tutte le frequenze dei dati problematici è la seguente: