Funzione di densità

Di Benjamin anderson Agosto 5, 2023 Probabilità 0 commenti

In questo articolo scoprirai cos’è la funzione di densità, come si calcola una probabilità dalla funzione di densità e le caratteristiche di questa funzione probabilistica. Inoltre, sarai in grado di vedere quali sono le differenze tra la funzione di densità e la funzione di distribuzione.

Qual è la funzione di densità?

La funzione di densità , detta anche funzione di densità di probabilità , è una funzione matematica che descrive la probabilità che una variabile casuale continua assuma un determinato valore.

In altre parole, la funzione di densità associata ad una variabile definisce matematicamente le probabilità che la variabile assuma un valore.

Ad esempio, supponiamo che la probabilità che una persona adulta sia più alta di 1,80 m in una popolazione sia del 35%, quindi la funzione di densità indicherà una probabilità del 35% nel calcolo di tale probabilità.

A volte la funzione di densità di probabilità è abbreviata in PDF.

Calcolare una probabilità con la funzione di densità

Per trovare la probabilità che una variabile continua assuma un valore in un intervallo è necessario calcolare l’integrale della funzione di densità associata a detta variabile tra i limiti dell’intervallo.

$\displaystyle P[a\leq X\leq b]=\int_a^b f(x)dx$

Oro

$f(x)$

è la funzione di densità della variabile casuale continua.

O in altre parole, la probabilità che la variabile assuma un valore in un intervallo è equivalente all’area sottesa alla funzione di densità in quell’intervallo.

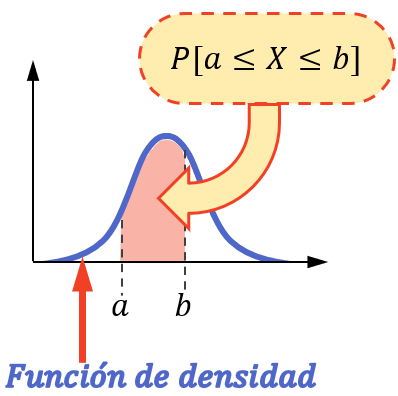
Si noti che il calcolo della probabilità può essere effettuato in questo modo solo se la variabile statistica segue una distribuzione continua, come la distribuzione normale, la distribuzione esponenziale, la distribuzione di Poisson, ecc.

Proprietà della funzione di densità

La funzione di densità ha le seguenti proprietà:

Il valore della funzione di densità è zero o positivo per qualsiasi valore di x.

$f(x)\geq 0$

Inoltre, il valore massimo della funzione di densità è uguale a 1.

$f(x)\leq 1$

Infatti, l’area totale sotto il grafico della funzione di densità è sempre equivalente a 1 indipendentemente dalla variabile, poiché corrisponde all’insieme di tutte le probabilità.

$\displaystyle \int_{-\infty}^{+\infty} f(x)dx=1$

Come spiegato nella sezione precedente, la probabilità che una variabile continua assuma un valore in un intervallo si calcola con l’integrale della funzione di densità in quell’intervallo.

$\displaystyle P[a\leq X\leq b]=\int_a^b f(x)dx=F(b)-F(a)$

Funzione di densità e funzione di distribuzione

In quest’ultima sezione vedremo come differiscono la funzione di densità e la funzione di distribuzione, poiché sono due tipi di funzioni probabilistiche generalmente confuse.

Matematicamente, la funzione di distribuzione è equivalente all’integrale della funzione di densità , quindi la funzione di distribuzione descrive la probabilità cumulativa di una variabile continua.

Cioè, l’immagine della funzione di distribuzione per qualsiasi valore è uguale alla probabilità che la variabile assuma quel valore o un valore inferiore.

La relazione matematica tra questi due tipi di funzioni è quindi la seguente:

$\displaystyle P[X\leq a]=\int_{-\infty}^a f(x)dx=F(a)$

Oro

$f(x)$

è la funzione di densità e

$F(x)$

è la funzione di distribuzione.

Nota come cambia la rappresentazione grafica della funzione di densità rispetto alla sua funzione di distribuzione di una variabile che segue una distribuzione normale con una media di 1 e una deviazione standard di 0,5:

differenza tra funzione di distribuzione e funzione di densità

Per ulteriori informazioni sulla funzionalità di distribuzione, fare clic sul collegamento seguente:

➤ Vedi: funzione di distribuzione

Informazioni sull'autore

Benjamin anderson

Ciao, sono Benjamin, un professore di statistica in pensione diventato insegnante dedicato di Statorials. Con una vasta esperienza e competenza nel campo della statistica, sono ansioso di condividere le mie conoscenze per potenziare gli studenti attraverso Statorials. Scopri di più