Come utilizzare la funzione lm() in r per adattare modelli lineari

La funzione lm() in R viene utilizzata per adattare i modelli di regressione lineare.

Questa funzione utilizza la seguente sintassi di base:

lm(formula, dati, …)

Oro:

• formula: la formula del modello lineare (ad esempio y ~ x1 + x2)
• dati: il nome del blocco dati che contiene i dati

L’esempio seguente mostra come utilizzare questa funzione in R per eseguire le seguenti operazioni:

• Adattare un modello di regressione
• Visualizza il riepilogo dell’adattamento del modello di regressione
• Visualizza i grafici diagnostici del modello
• Tracciare il modello di regressione adattato
• Effettua previsioni utilizzando il modello di regressione

Adattare il modello di regressione

Il codice seguente mostra come utilizzare la funzione lm() per adattare un modello di regressione lineare in R:

 #define data
df = data. frame (x=c(1, 3, 3, 4, 5, 5, 6, 8, 9, 12),
                y=c(12, 14, 14, 13, 17, 19, 22, 26, 24, 22))

#fit linear regression model using 'x' as predictor and 'y' as response variable
model <- lm(y ~ x, data=df)

Mostra riepilogo del modello di regressione

Possiamo quindi utilizzare la funzione summary() per visualizzare il riepilogo dell’adattamento del modello di regressione:

 #view summary of regression model
summary(model)

Call:
lm(formula = y ~ x, data = df)

Residuals:
    Min 1Q Median 3Q Max 
-4.4793 -0.9772 -0.4772 1.4388 4.6328 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) 11.1432 1.9104 5.833 0.00039 ***
x 1.2780 0.2984 4.284 0.00267 ** 
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 2.929 on 8 degrees of freedom
Multiple R-squared: 0.6964, Adjusted R-squared: 0.6584 
F-statistic: 18.35 on 1 and 8 DF, p-value: 0.002675

Ecco come interpretare i valori più importanti nel modello:

• Statistica F = 18,35, valore p corrispondente = 0,002675. Poiché questo valore p è inferiore a 0,05, il modello nel suo insieme è statisticamente significativo.
• Multiplo R quadrato = 0,6964. Questo ci dice che il 69,64% della variazione nella variabile di risposta, y, può essere spiegato dalla variabile predittrice, x.
• Coefficiente stimato di x : 1,2780. Questo ci dice che ogni ulteriore aumento unitario di x è associato a un aumento medio di 1,2780 in y.

Possiamo quindi utilizzare le stime dei coefficienti dall’output per scrivere l’equazione di regressione stimata:

y = 11,1432 + 1,2780*(x)

Bonus : puoi trovare una guida completa per interpretare ciascun valore dell’output della regressione in R qui .

Visualizza i grafici diagnostici del modello

Possiamo quindi utilizzare la funzione plot() per tracciare i grafici diagnostici del modello di regressione:

 #create diagnostic plots
plot(model) 

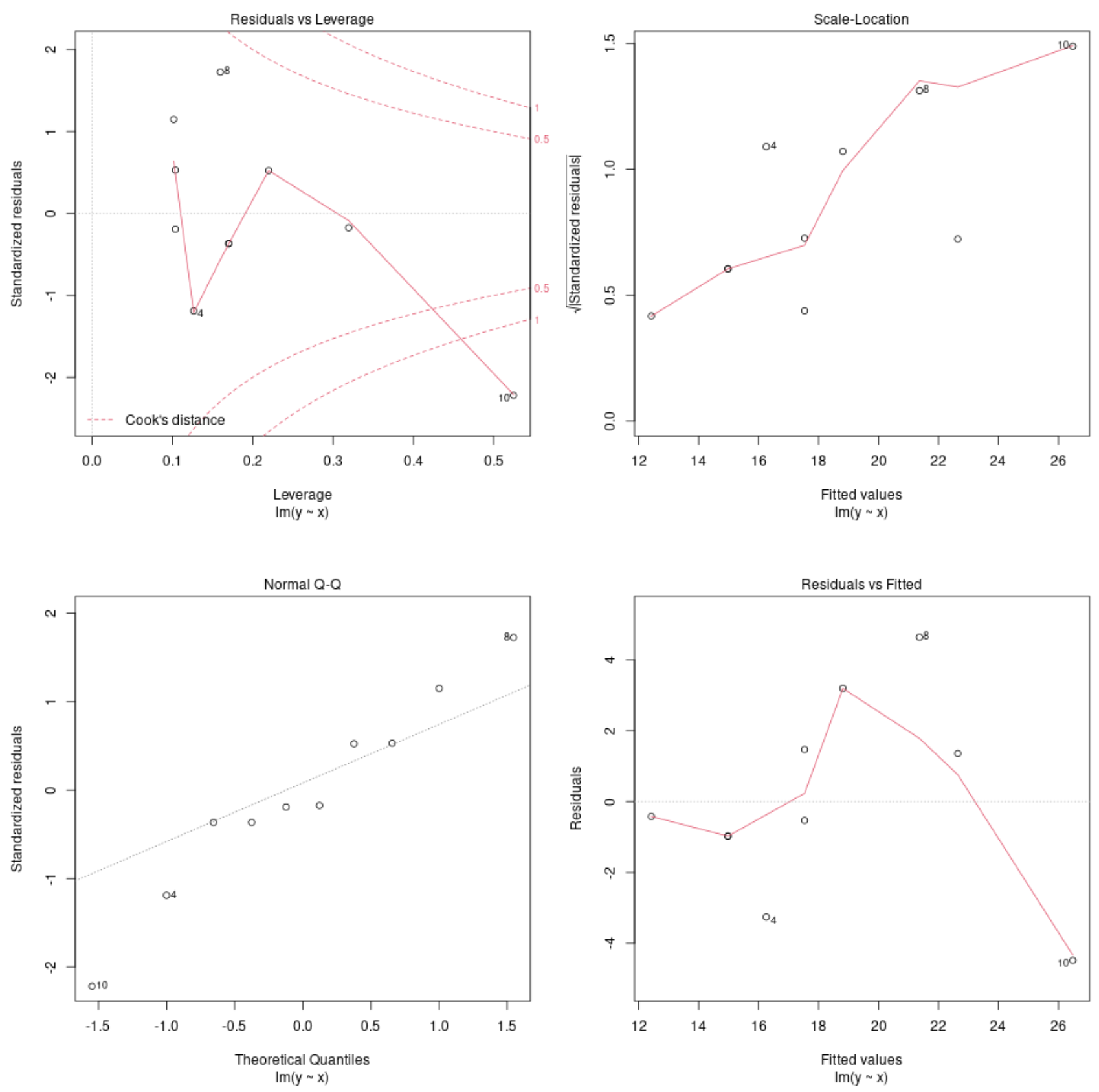
Questi grafici ci consentono di analizzare i residui del modello di regressione per determinare se il modello è appropriato da utilizzare per i dati.

Fare riferimento a questo tutorial per una spiegazione completa su come interpretare i grafici diagnostici di un modello in R.

Tracciare il modello di regressione adattato

Possiamo usare la funzione abline() per tracciare il modello di regressione adattato:

 #create scatterplot of raw data
plot(df$x, df$y, col=' red ', main=' Summary of Regression Model ', xlab=' x ', ylab=' y ')

#add fitted regression line
abline(model)

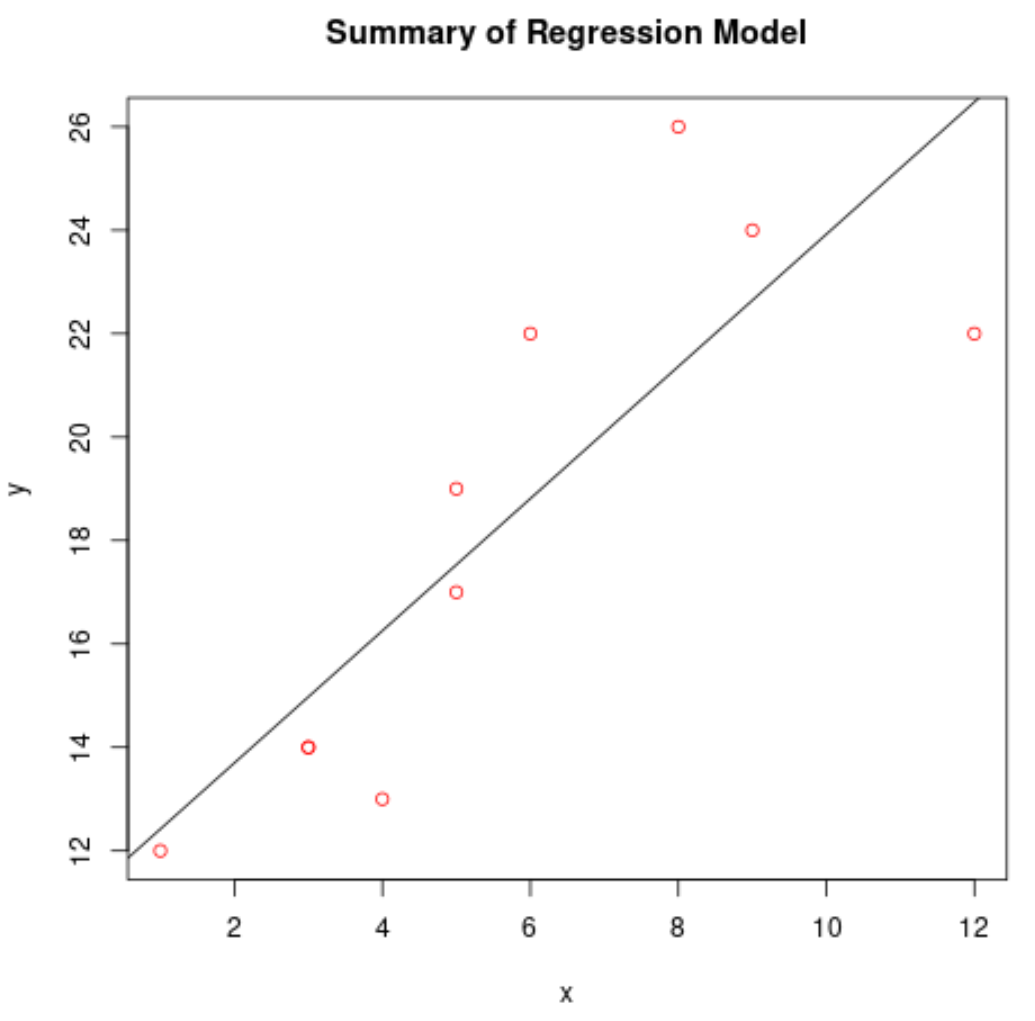
Utilizzare il modello di regressione per fare previsioni

Possiamo utilizzare la funzione predit() per prevedere il valore di risposta per una nuova osservazione:

 #define new observation
new <- data. frame (x=c(5))

#use the fitted model to predict the value for the new observation
predict(model, newdata = new)

      1 
17.5332

Il modello prevede che questa nuova osservazione avrà un valore di risposta di 17.5332 .

Risorse addizionali

Come eseguire una regressione lineare semplice in R
Come eseguire la regressione lineare multipla in R
Come eseguire la regressione graduale in R