Come utilizzare geometpdf() e geometcdf() su una calcolatrice ti-84

La distribuzione geometrica descrive la probabilità di sperimentare un certo numero di fallimenti prima di sperimentare il primo successo in una serie di prove con le seguenti caratteristiche:

• Ci sono solo due esiti possibili: successo o fallimento.
• La probabilità di successo è la stessa in ogni prova.

Se una variabile casuale X segue una distribuzione geometrica, la probabilità di sperimentare k fallimenti prima di sperimentare il primo successo può essere trovata dalla seguente formula:

P(X=k) = (1-p) ^kp

Oro:

• k: numero di fallimenti prima del primo successo
• p: probabilità di successo in ciascuna prova

La probabilità cumulativa di riscontrare k o meno fallimenti fino al primo successo può essere trovata utilizzando la seguente formula:

P(X≤k) = 1 – (1-p) ^k+1

Per calcolare le probabilità legate alla distribuzione geometrica su una calcolatrice TI-84, è possibile utilizzare le seguenti funzioni:

• geometpdf (probabilità, test)
• geometcdf(probabilità, test)

Gli esempi seguenti mostrano come utilizzare nella pratica ciascuna di queste funzioni.

Esempio 1: come utilizzare geometpdf()

Supponiamo che un ricercatore aspetti fuori da una biblioteca per chiedere alle persone se sostengono una determinata legge. La probabilità che una determinata persona sostenga la legge è p = 0,2. Qual è la probabilità che la quarta persona con cui parla il ricercatore sia la prima a sostenere la legge?

Per rispondere a questa domanda possiamo utilizzare la funzione geometpdf() .

Premere 2nd quindi premere VARS . Scorri fino a geometpdf() e premi INVIO .

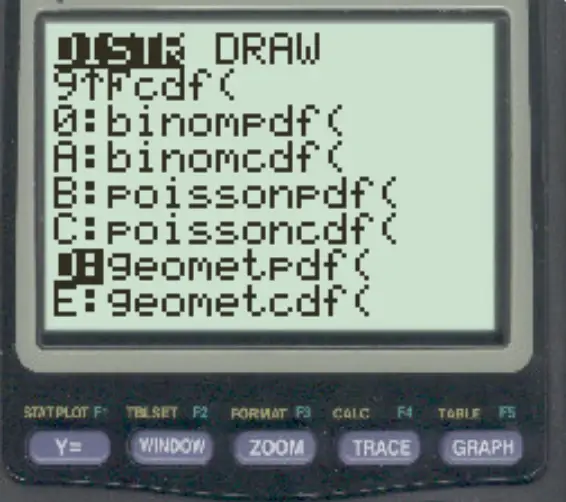
Digitare quindi i seguenti valori e premere INVIO .

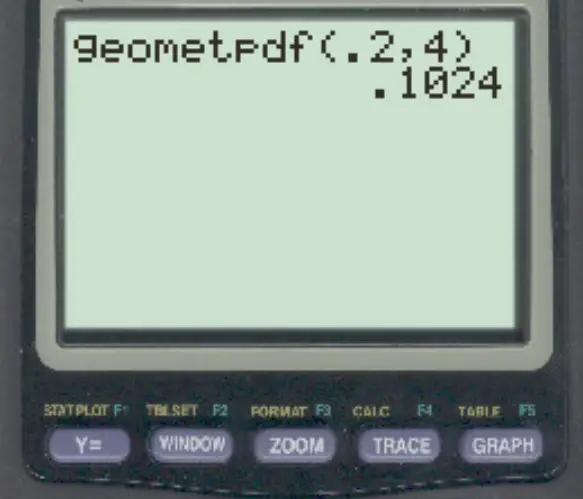
La probabilità che la quarta persona con cui parla il ricercatore sia la prima a sostenere la legge è 0,1024 .

Esempio 2: come utilizzare geometcdf()

Supponiamo di sapere che il 4% delle persone che visitano una certa banca lo fanno per dichiarare bancarotta. Qual è la probabilità che il banchiere incontri meno di 9 persone prima di incontrare qualcuno che dichiara bancarotta?

Per rispondere a questa domanda possiamo utilizzare la funzione geometcdf() .

Premere 2nd quindi premere VARS . Scorri verso il basso fino a geometcdf() e premi INVIO .

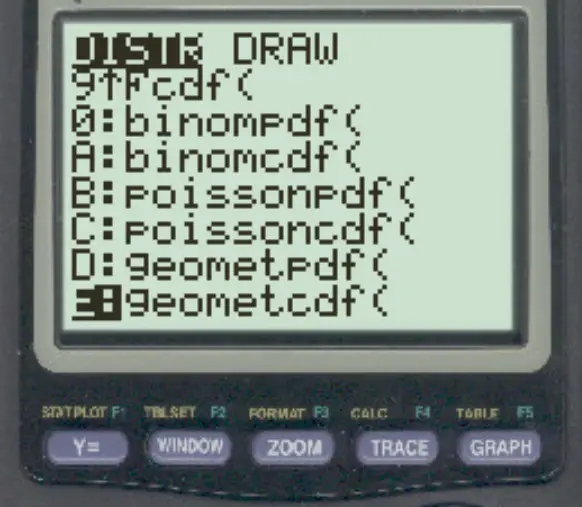
Digitare quindi i seguenti valori e premere INVIO .

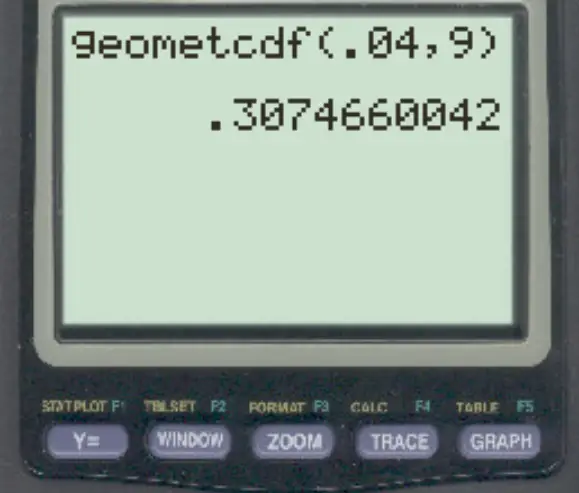
La probabilità che il banchiere incontri meno di 9 persone prima di incontrare qualcuno che dichiari bancarotta è 0,307466 .

Bonus: sentiti libero di utilizzare questo calcolatore di distribuzione geometrica online per confermare i tuoi risultati.

Risorse addizionali

Come calcolare le probabilità normali su una calcolatrice TI-84
Come calcolare le probabilità binomiali su una calcolatrice TI-84
Come calcolare le probabilità di Poisson su una calcolatrice TI-84