Come calcolare gli intervalli di confidenza in excel
Un intervallo di confidenza è un intervallo di valori che probabilmente contiene un parametro della popolazione con un certo livello di confidenza. Si calcola secondo la seguente formula generale:
Intervallo di confidenza = (stima puntuale) +/- (valore critico)* (errore standard)
Questa formula crea un intervallo con un limite inferiore e un limite superiore, che probabilmente contiene un parametro della popolazione con un certo livello di confidenza:
Intervallo di confidenza = [limite inferiore, limite superiore]
Questo tutorial spiega come calcolare i seguenti intervalli di confidenza in Excel:
1. Intervallo di confidenza per una media
2. Intervallo di confidenza per una differenza di medie
3. Intervallo di confidenza per una proporzione
4. Intervallo di confidenza per una differenza nelle proporzioni
Andiamo!
Esempio 1: intervallo di confidenza per una media
Usiamo la seguente formula per calcolare un intervallo di confidenza per una media :
Intervallo di confidenza = x +/- z*(s/√n)
Oro:
- x : media campionaria
- z: il valore z scelto
- s: deviazione standard campionaria
- n: dimensione del campione
Esempio: supponiamo di raccogliere un campione casuale di tartarughe con le seguenti informazioni:
- Dimensione del campione n = 25
- Peso medio del campione x = 300
- Deviazione standard del campione s = 18,5
La schermata seguente mostra come calcolare un intervallo di confidenza al 95% per il peso medio reale della popolazione di tartarughe:
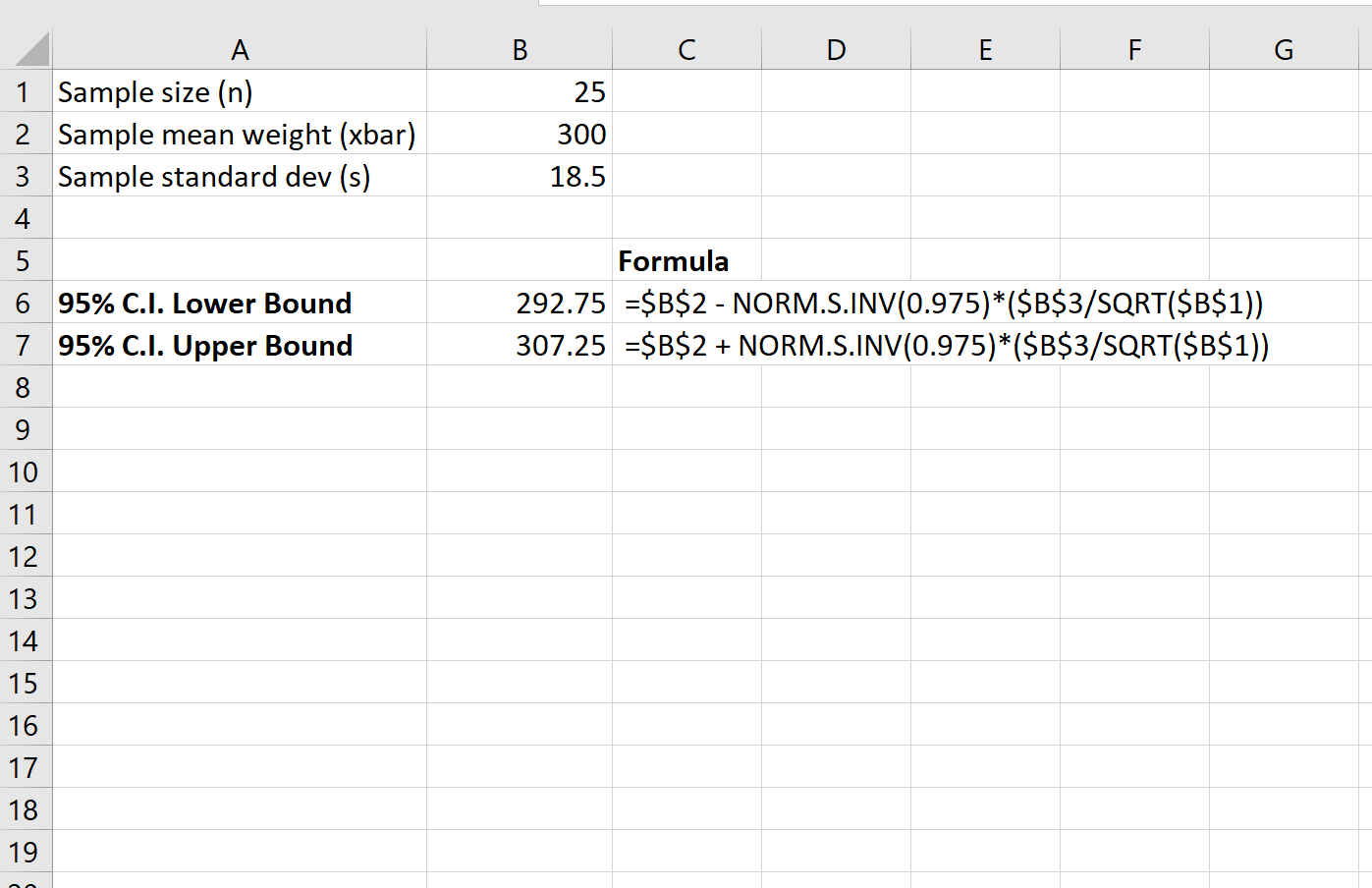
L’intervallo di confidenza al 95% per il peso medio reale della popolazione delle tartarughe è [292,75, 307,25] .
Esempio 2: intervallo di confidenza per una differenza nelle medie
Usiamo la seguente formula per calcolare un intervallo di confidenza per una differenza nelle medie della popolazione :
Intervallo di confidenza = ( x 1 – x 2 ) +/- t*√((s p 2 /n 1 ) + (s p 2 /n 2 ))
Oro:
- x 1 , x 2 : media del campione 1, media del campione 2
- t: il valore t-critico basato sul livello di confidenza e (n 1 + n 2 -2) gradi di libertà
- s p 2 : varianza aggregata, calcolata come ((n 1 -1)s 1 2 + (n 2 -1)s 2 2 ) / (n 1 +n 2 -2)
- t: il valore t-critico
- n1 , n2 : dimensione del campione 1, dimensione del campione 2
Esempio: Supponiamo di voler stimare la differenza di peso medio tra due diverse specie di tartarughe. Raccogliamo quindi un campione casuale di 15 tartarughe da ciascuna popolazione. Ecco i dati riepilogativi per ciascun campione:
Esempio 1:
- x1 = 310
- s1 = 18,5
- n1 = 15
Esempio 2:
- x2 = 300
- s2 = 16,4
- n2 = 15
La schermata seguente mostra come calcolare un intervallo di confidenza al 95% per la vera differenza nelle medie della popolazione:
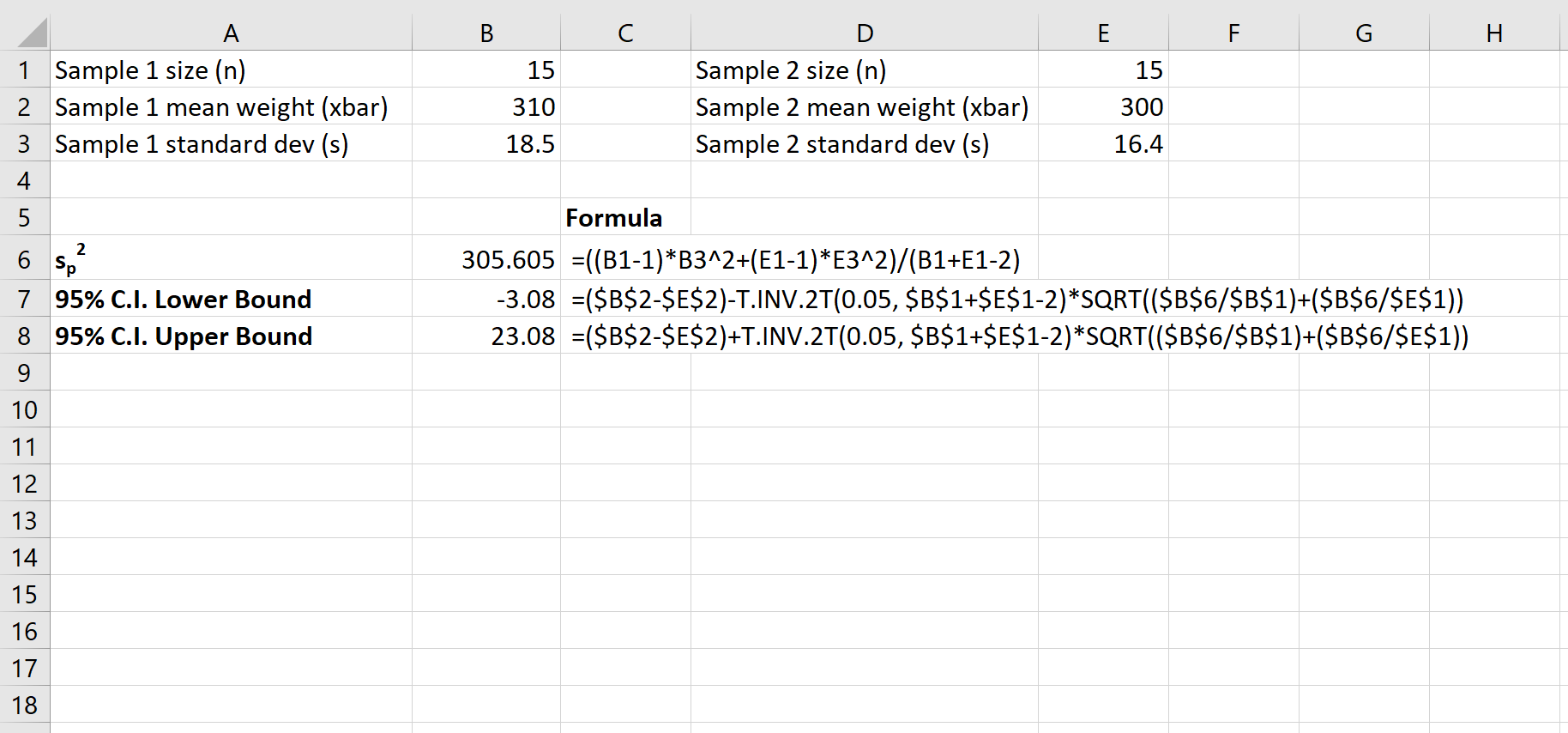
L’intervallo di confidenza al 95% per la differenza reale tra le medie della popolazione è [-3,08, 23,08] .
Esempio 3: intervallo di confidenza per una proporzione
Usiamo la seguente formula per calcolare un intervallo di confidenza per una proporzione :
Intervallo di confidenza = p +/- z*√ p(1-p) / n
Oro:
- p: proporzione del campione
- z: il valore z scelto
- n: dimensione del campione
Esempio: supponiamo di voler stimare la percentuale di residenti in una contea che sono favorevoli ad una determinata legge. Selezioniamo un campione casuale di 100 residenti e chiediamo loro quale sia la loro posizione rispetto alla legge. Ecco i risultati:
- Dimensione del campione n = 100
- Proporzione a favore della legge p = 0,56
Lo screenshot seguente mostra come calcolare un intervallo di confidenza del 95% per la percentuale reale di residenti in tutta la contea che sono a favore della legge:
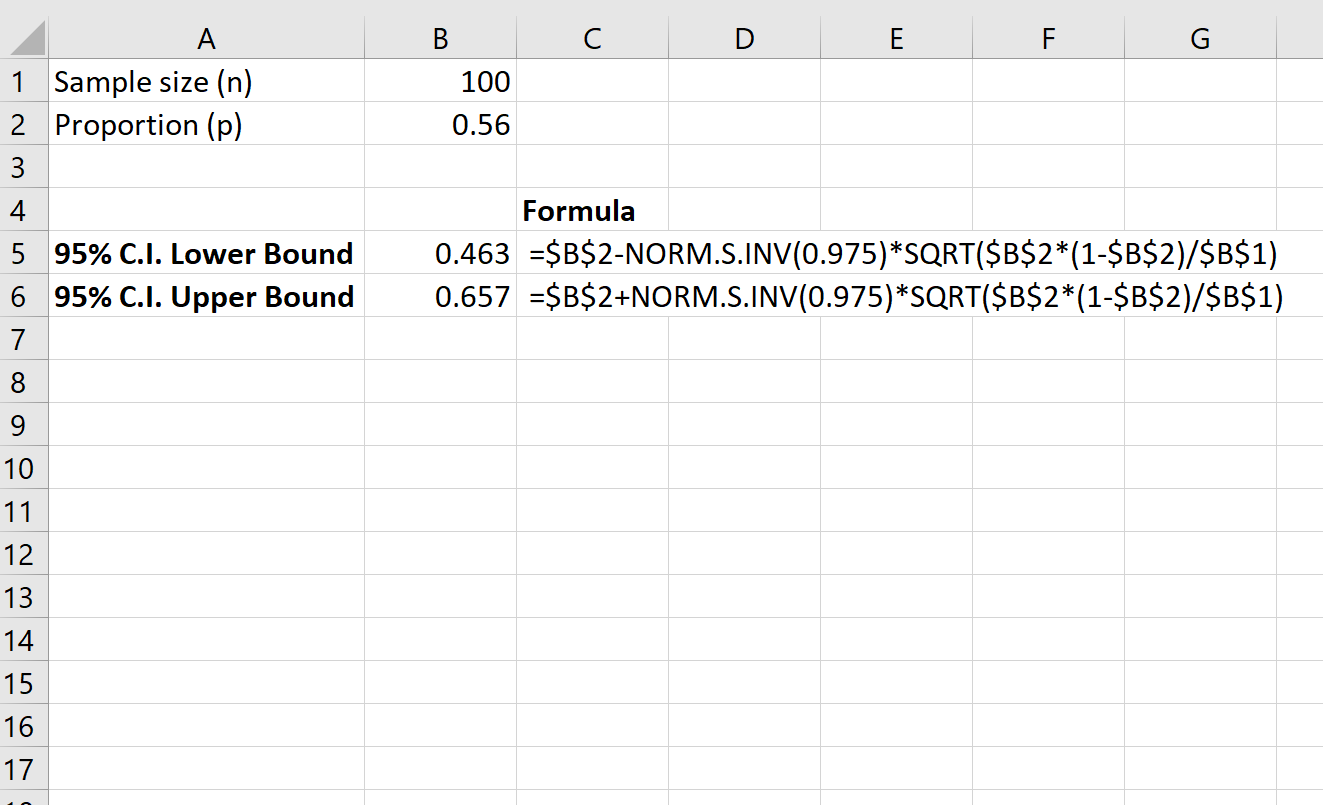
L’intervallo di confidenza del 95% per la percentuale reale di residenti in tutta la contea che sono a favore della legge è [.463, .657] .
Esempio 4: intervallo di confidenza per una differenza nelle proporzioni
Usiamo la seguente formula per calcolare un intervallo di confidenza per una differenza nelle proporzioni :
Intervallo di confidenza = (p 1 –p 2 ) +/- z*√(p 1 (1-p 1 )/n 1 + p 2 (1-p 2 )/n 2 )
Oro:
- p 1 , p 2 : proporzione del campione 1, proporzione del campione 2
- z: il valore z-critico basato sul livello di confidenza
- n1 , n2 : dimensione del campione 1, dimensione del campione 2
Esempio: supponiamo di voler stimare la differenza tra la percentuale di residenti che sostengono una determinata legge nella contea A rispetto alla proporzione che sostiene la legge nella contea B. Ecco i dati riepilogativi per ciascun campione:
Esempio 1:
- n1 = 100
- p 1 = 0,62 (ovvero 62 abitanti su 100 sostengono la legge)
Esempio 2:
- n2 = 100
- p 2 = 0,46 (ovvero 46 abitanti su 100 sostengono la legge)
Lo screenshot seguente mostra come calcolare un intervallo di confidenza del 95% per la differenza reale nella percentuale di residenti che sostengono la legge tra le contee:
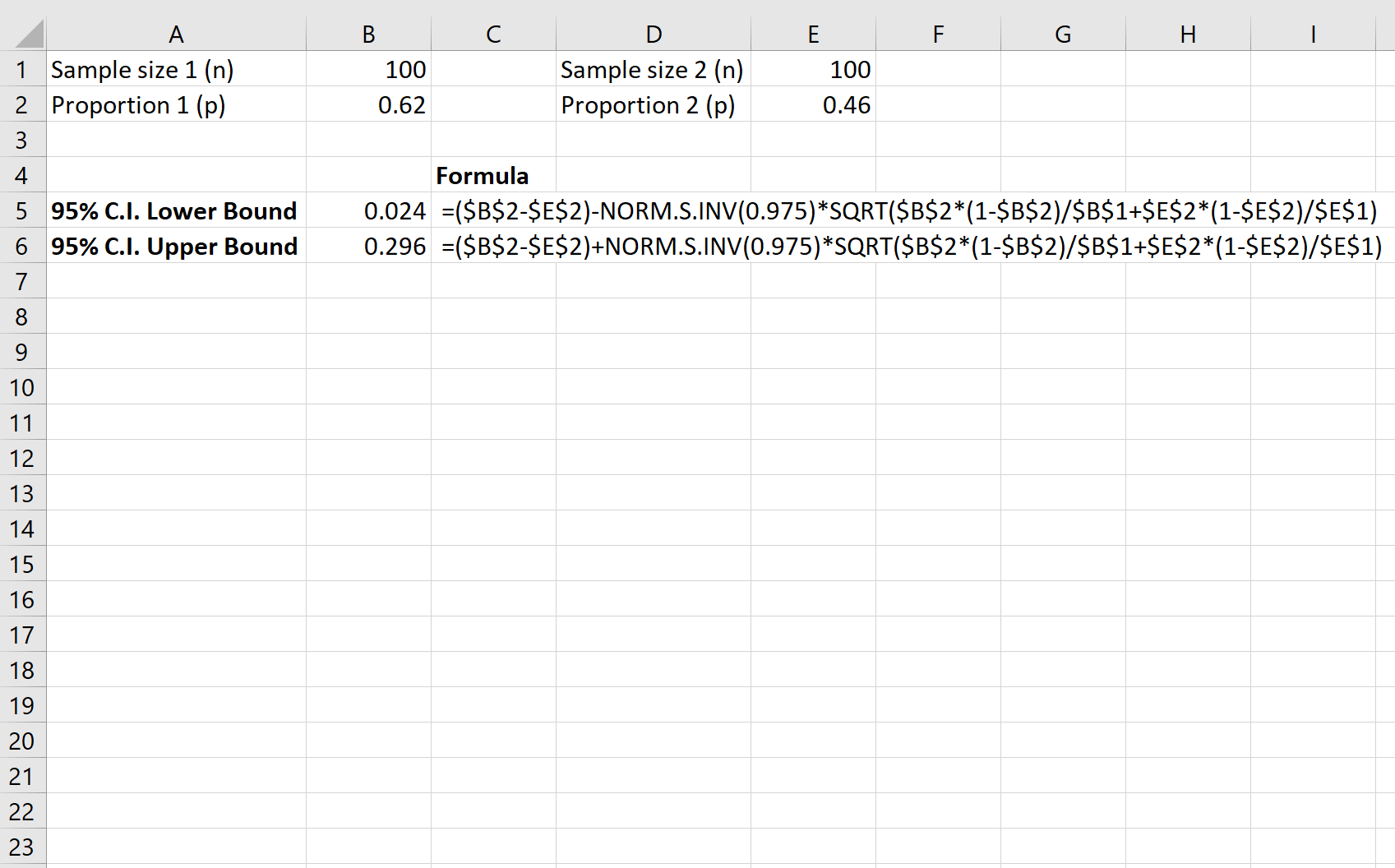
L’ intervallo di confidenza del 9,5% per la differenza reale nella percentuale di residenti che sostengono la legge tra le contee è [0,024, 0,296] .
Puoi trovare altri tutorial su Excel qui .
Informazioni sull'autore
Benjamin anderson
Ciao, sono Benjamin, un professore di statistica in pensione diventato insegnante dedicato di Statorials. Con una vasta esperienza e competenza nel campo della statistica, sono ansioso di condividere le mie conoscenze per potenziare gli studenti attraverso Statorials. Scopri di più