Come creare manualmente un percorso residuo

Un grafico dei residui è un tipo di grafico che visualizza i valori di una variabile predittrice in un modello di regressione lungo l’asse x e i valori dei residui lungo l’asse y.

Questo grafico viene utilizzato per valutare se i residui di un modello di regressione sono normalmente distribuiti e se presentano o meno eteroschedasticità .

Il seguente esempio passo passo mostra come creare manualmente un grafico dei residui per un modello di regressione.

Passaggio 1: trovare i valori previsti

Supponiamo di voler adattare un modello di regressione al seguente set di dati:

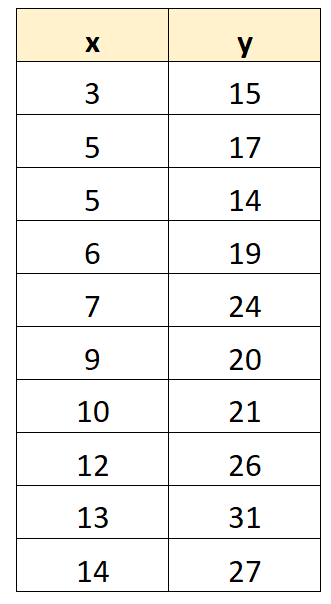
Utilizzando software statistico (come Excel, R, Python, SPSS, ecc.), possiamo vedere che il modello di regressione adattato è:

y = 10,4486 + 1,3037(x)

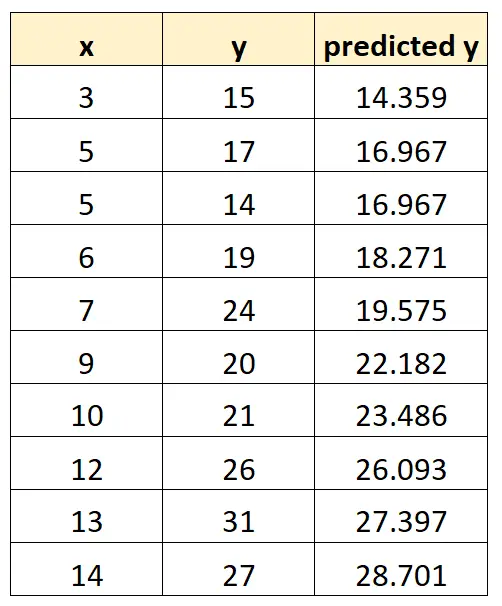
Possiamo quindi utilizzare questo modello per prevedere il valore di y, in base al valore di x. Ad esempio, se x = 3, allora prevediamo che y sarà:

y = 10,4486 + 1,3037(3) = 14,359

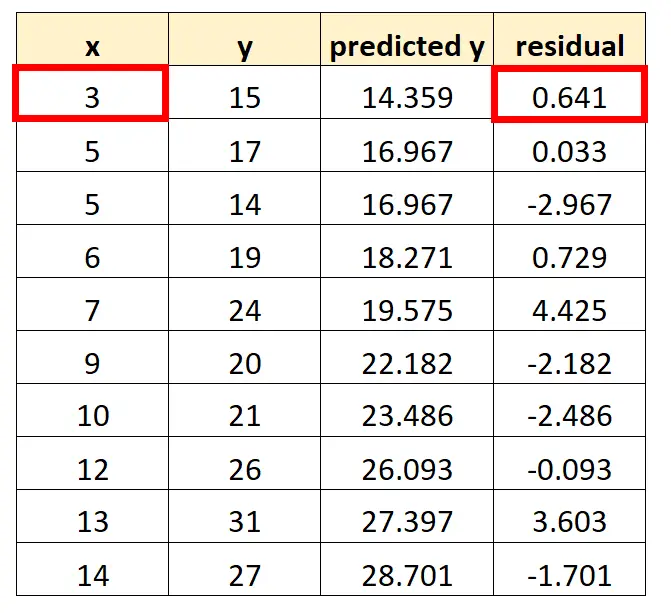
Possiamo ripetere questo processo per ogni osservazione nel nostro set di dati:

Passaggio 2: trova i residui

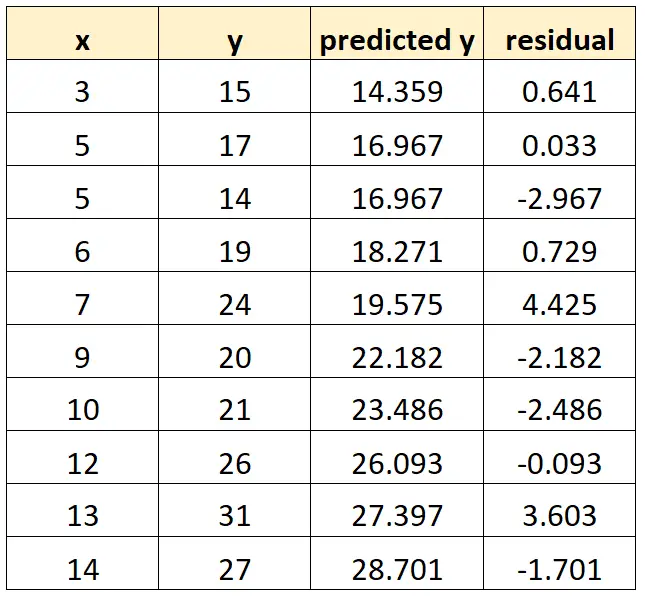
Un residuo per una data osservazione nel nostro set di dati viene calcolato come segue:

Residuo = valore osservato – valore previsto

Ad esempio, il residuo della prima osservazione verrebbe calcolato come segue:

Residuo = 15 – 14,359 = 0,641

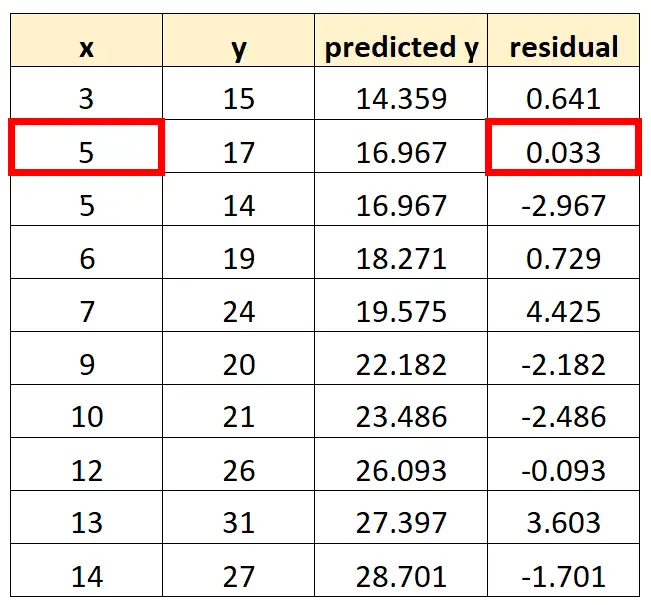
Possiamo ripetere questo processo per ogni osservazione nel nostro set di dati:

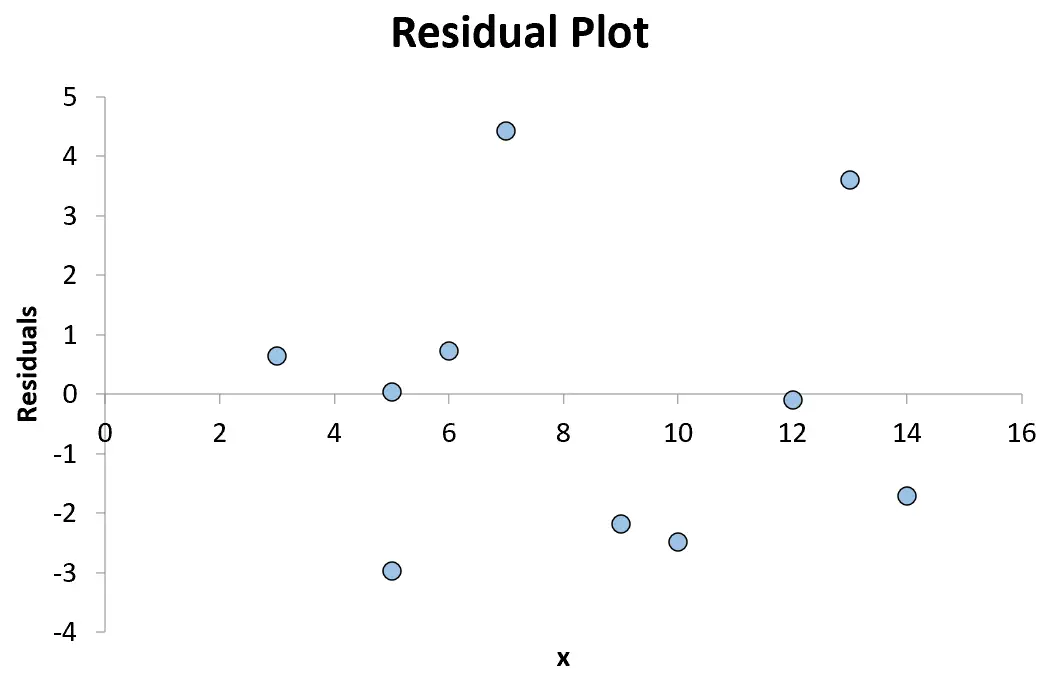
Passaggio 3: creare la trama residua

Infine, possiamo creare un grafico dei residui posizionando i valori x lungo l’asse x e i residui lungo l’asse y.

Ad esempio, il primo punto che inseriremo nel nostro grafico è (3, 0,641)

Il prossimo punto che inseriremo nel nostro grafico è (5, 0,033)

Continueremo finché non avremo inserito tutte le 10 combinazioni a coppie di valori x e residui nel grafico:

Qualsiasi punto sopra lo zero nel grafico rappresenta un residuo positivo. Ciò significa che il valore osservato per y è maggiore del valore previsto dal modello di regressione.

Qualsiasi punto inferiore a zero rappresenta un residuo negativo. Ciò significa che il valore osservato per y è inferiore al valore previsto dal modello di regressione.

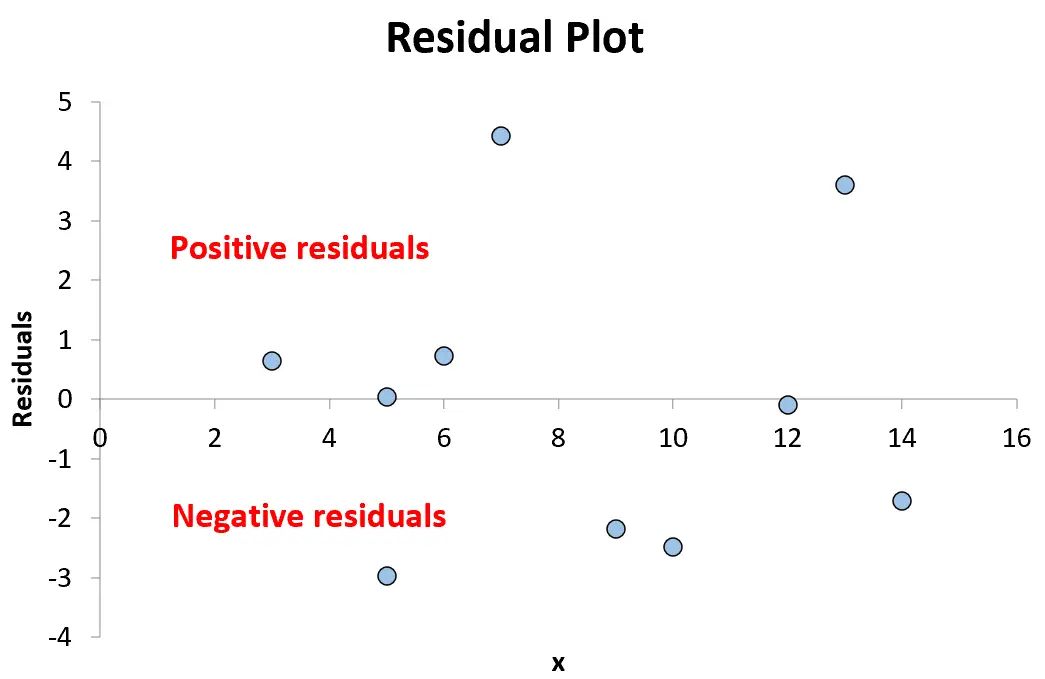
Poiché i punti sul grafico sono sparsi in modo casuale attorno a un residuo di 0 senza uno schema chiaro, ciò indica che la relazione tra xey è lineare ed è appropriato utilizzare un modello di regressione lineare.

E poiché i residui non aumentano o diminuiscono sistematicamente all’aumentare della variabile predittrice, ciò significa che l’eteroschedasticità non è un problema con questo modello di regressione.

Risorse addizionali

I seguenti tutorial spiegano come creare grafici dei residui utilizzando diversi software statistici:

Come creare un grafico residuo su una calcolatrice TI-84
Come creare un grafico residuo in Excel
Come creare una trama residua in R
Come creare un grafico residuo in Python