Grafico a dispersione

Questo articolo spiega cosa sono i grafici a dispersione. Scoprirai quindi a cosa serve una nuvola di punti, come crearla, come interpretarla ed esempi di nuvole di punti.

Cos’è una nuvola di punti?

Il grafico a dispersione , o diagramma a dispersione , è un tipo di diagramma statistico in cui un insieme di dati di due variabili viene rappresentato graficamente su due assi di coordinate cartesiane.

Pertanto, i grafici a dispersione vengono utilizzati per analizzare la relazione tra due variabili statistiche.

I grafici a dispersione hanno diversi nomi, ad esempio diagramma di correlazione o diagramma a dispersione .

Va notato che il diagramma di dispersione è considerato uno degli strumenti fondamentali del controllo di qualità, proprio come il diagramma di Pareto, il diagramma di causa ed effetto, il diagramma di flusso, ecc.

Come realizzare un grafico a dispersione

Per creare un grafico a dispersione, è necessario seguire i seguenti passaggi:

1. Raccogli dati statistici dal campione che desideri analizzare. Tieni presente che per creare un grafico a dispersione devono essere presenti almeno due variabili quantitative.
2. Traccia i due assi del grafico a dispersione.
3. Determinare le due variabili statistiche che verranno rappresentate graficamente.
4. Calibrare la scala di ciascun asse del grafico. Per fare ciò, si consiglia di trovare prima il minimo e il massimo di ciascuna variabile e, in base a questi valori, scalare ciascun asse.
5. Rappresenta ogni coppia di dati sul grafico a dispersione con un punto.
6. Analizzare e interpretare il diagramma di dispersione ottenuto.

Esempio di grafico a dispersione

Dopo aver visto la definizione di diagramma a dispersione e la teoria sulla sua realizzazione, in questa sezione viene rappresentato come esempio un diagramma di questo tipo.

• Nella seguente tabella di frequenza sono stati raccolti come dati i punteggi in matematica e statistica di un campione di 20 studenti. Traccia il set di dati su un grafico a dispersione e analizzalo.

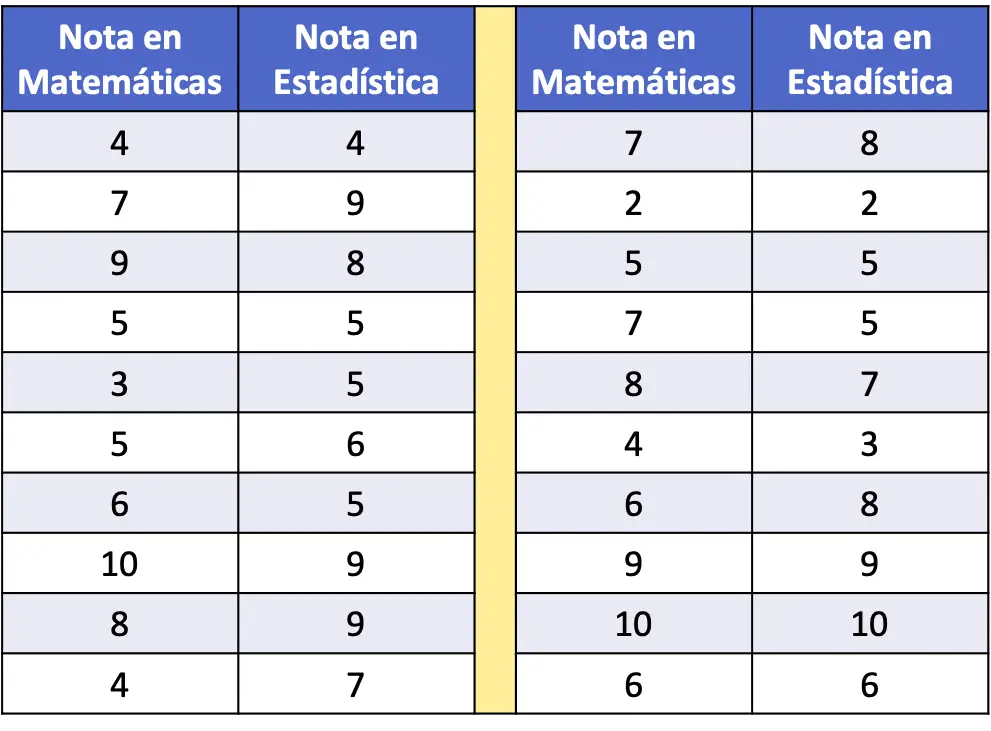
Per rappresentare la serie di dati in un grafico a dispersione, dobbiamo semplicemente tracciare due assi, calibrarli e tracciare un punto sul grafico per ciascuna coppia di dati. Ricorda che un punto su un grafico è posizionato all’intersezione delle linee immaginarie corrispondenti a ciascuno dei suoi valori.

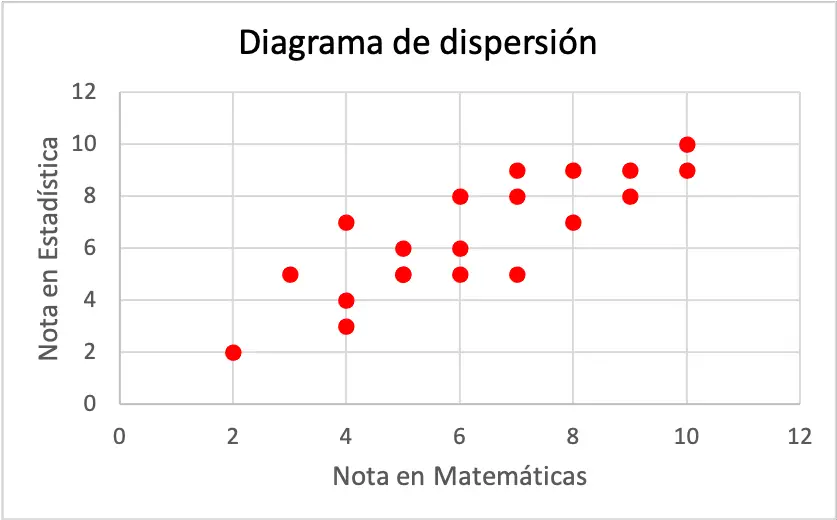
Ciascun asse del grafico a dispersione rappresenta una variabile. Più precisamente, l’asse orizzontale corrisponde al voto ottenuto in matematica e, invece, l’asse verticale corrisponde al voto ottenuto in statistica.

Come puoi vedere dal grafico a dispersione, le due variabili hanno una correlazione positiva, perché una variabile aumenta all’aumentare dell’altra variabile. Pertanto, si conclude che se uno studente ottiene un voto migliore in matematica, è più probabile che ottenga un voto migliore anche in statistica, e viceversa.

Tuttavia, la conclusione precedente non significa che una variabile sia causa dell’altra, perché prendere un buon voto in matematica non garantisce automaticamente un buon voto in statistica senza fare nulla, ma bisognerebbe studiare entrambe le materie. Nella prossima sezione approfondiremo questo concetto.

Il grafico a dispersione e la correlazione

Da un diagramma di dispersione è possibile identificare il tipo di correlazione tra due variabili:

• Correlazione diretta (o correlazione positiva) : una variabile aumenta quando aumenta anche l’altra.
• Correlazione inversa (o correlazione negativa) : quando una variabile aumenta, l’altra diminuisce, e viceversa, se una variabile diminuisce, l’altra aumenta.
• Correlazione zero (nessuna correlazione) : non esiste alcuna relazione tra le due variabili.

Allo stesso modo, indipendentemente dal fatto che la correlazione tra le due variabili sia diretta o inversa, la correlazione può anche essere classificata in base alla forza o alla debolezza della relazione tra le due variabili.

• Correlazione forte: le due variabili sono strettamente legate. I punti vengono riuniti nella nuvola di punti. Ciò rende più semplice identificare la relazione tra le variabili.
• Bassa correlazione : esiste una relazione tra le due variabili, ma è difficile da identificare. I punti sono distanti tra loro sulla nuvola di punti.

D’altra parte, la correlazione può anche essere calcolata numericamente utilizzando una formula, che consente di sapere matematicamente quanto siano strettamente correlate due diverse variabili. Per vedere come funziona, clicca sul seguente link:

Tieni presente che anche se esiste una correlazione tra due variabili, ciò non significa che esista causalità tra loro, ovvero la correlazione tra due variabili non significa che il cambiamento di una variabile sia la causa del cambiamento nell’altra. variabile.

Quindi, come nel grafico a dispersione della sezione precedente, sebbene esista una correlazione positiva tra voto in matematica e voto in statistica, ottenere un buon voto in matematica non significa ottenere un buon voto in statistica, perché se studi solo matematica, sicuramente fallirai nelle statistiche. Pertanto, le due variabili sono correlate ma non sono causa ed effetto.

Per saperne di più potete proseguire con il seguente post:

Vantaggi e svantaggi della nuvola di punti

A causa delle caratteristiche del grafico a dispersione, questo tipo di grafico statistico presenta vantaggi e svantaggi.

Vantaggio:

• È abbastanza semplice rappresentare una serie di dati su un grafico a dispersione.
• Il grafico a dispersione consente di analizzare visivamente la relazione tra due variabili, facilitando il trarre conclusioni.
• I grafici a dispersione possono essere utilizzati anche in uno studio statistico approfondito come esplorazione preliminare dei dati.

Svantaggi:

• Questi tipi di diagrammi non sono utili per rappresentare variabili qualitative.
• L’interpretazione di un grafico a dispersione può portare a una conclusione errata di causa ed effetto tra due variabili.
• I grafici a dispersione non consentono di analizzare la relazione tra più di due variabili.