Come creare un grafico residuo in python

Un diagramma dei residui è un tipo di diagramma che visualizza i valori adattati rispetto ai residui di un modello di regressione .

Questo tipo di grafico viene spesso utilizzato per valutare se un modello di regressione lineare è appropriato o meno per un dato set di dati e per verificare l’ eteroschedasticità dei residui.

Questo tutorial spiega come creare un grafico dei residui per un modello di regressione lineare in Python.

Esempio: trama dei residui in Python

Per questo esempio, utilizzeremo un set di dati che descrive gli attributi di 10 giocatori di basket:

 import numpy as np
import pandas as pd

#create dataset
df = pd.DataFrame({'rating': [90, 85, 82, 88, 94, 90, 76, 75, 87, 86],
                   'points': [25, 20, 14, 16, 27, 20, 12, 15, 14, 19],
                   'assists': [5, 7, 7, 8, 5, 7, 6, 9, 9, 5],
                   'rebounds': [11, 8, 10, 6, 6, 9, 6, 10, 10, 7]})

#view dataset
df

	rating points assists rebounds
0 90 25 5 11
1 85 20 7 8
2 82 14 7 10
3 88 16 8 6
4 94 27 5 6
5 90 20 7 9
6 76 12 6 6
7 75 15 9 10
8 87 14 9 10
9 86 19 5 7

Grafico dei residui per una regressione lineare semplice

Supponiamo di adattare un modello di regressione lineare semplice utilizzando i punti come variabile predittiva e il voto come variabile di risposta:

 #import necessary libraries
import matplotlib.pyplot as plt
import statsmodels.api as sm
from statsmodels.formula.api import ols

#fit simple linear regression model
model = ols('rating ~ points', data=df). fit ()

#view model summary
print(model.summary())

Possiamo creare un grafico residuo o adattato utilizzando la funzione plot_regress_exog() dalla libreria statsmodels:

 #define figure size
fig = plt.figure(figsize=(12,8))

#produce regression plots
fig = sm.graphics.plot_regress_exog(model, ' points ', fig=fig)

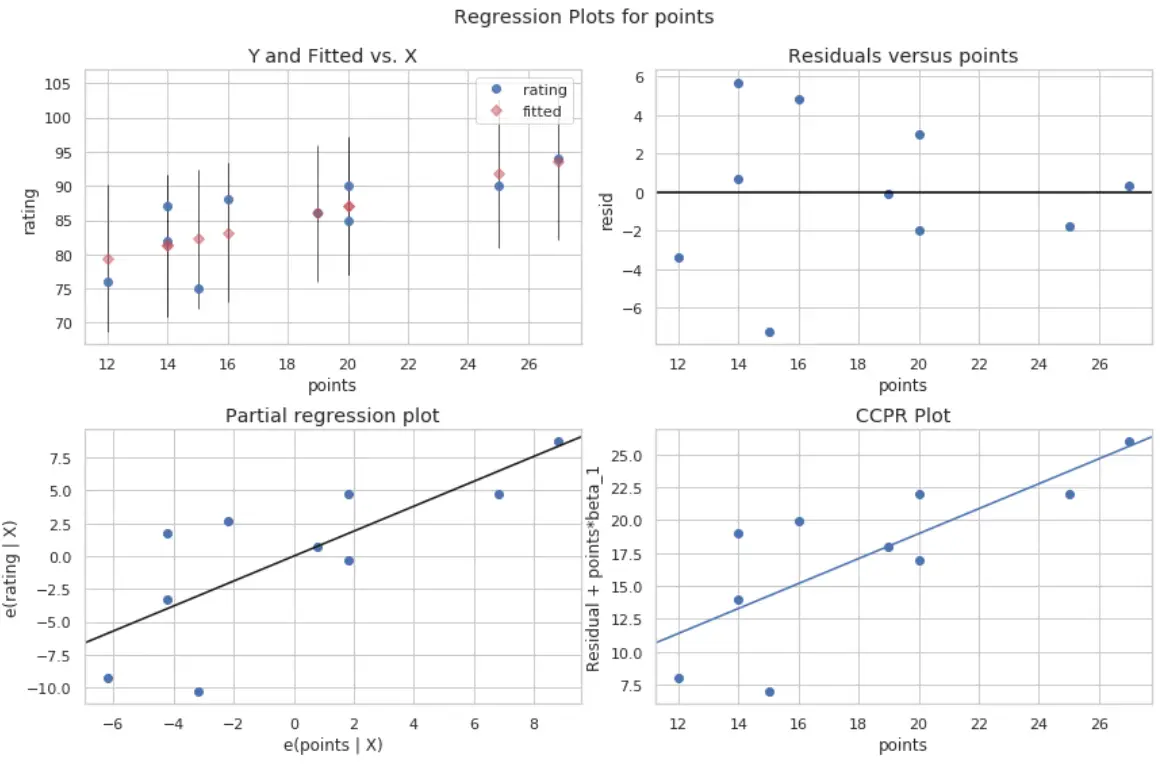
Vengono prodotti quattro appezzamenti. Quello nell’angolo in alto a destra è la trama residua rispetto alla trama modificata. L’asse x su questo grafico mostra i valori effettivi dei punti della variabile predittore e l’asse y mostra il residuo per quel valore.

Poiché i residui sembrano essere sparsi in modo casuale attorno allo zero, ciò indica che l’eteroschedasticità non è un problema con la variabile predittrice.

Grafici residui per regressione lineare multipla

Supponiamo invece di adattare un modello di regressione lineare multipla utilizzando assist e rimbalzi come variabile predittiva e valutazione come variabile di risposta:

 #fit multiple linear regression model
model = ols('rating ~ assists + rebounds', data=df). fit ()

#view model summary
print(model.summary())

Ancora una volta, possiamo creare un grafico dei residui rispetto a quello dei predittori per ciascuno dei singoli predittori utilizzando la funzione plot_regress_exog() dalla libreria statsmodels.

Ad esempio, questo è l’aspetto del grafico residui/predittore per gli assist delle variabili predittore:

 #create residual vs. predictor plot for 'assists'
fig = plt.figure(figsize=(12,8))
fig = sm.graphics.plot_regress_exog(model, ' assists ', fig=fig)

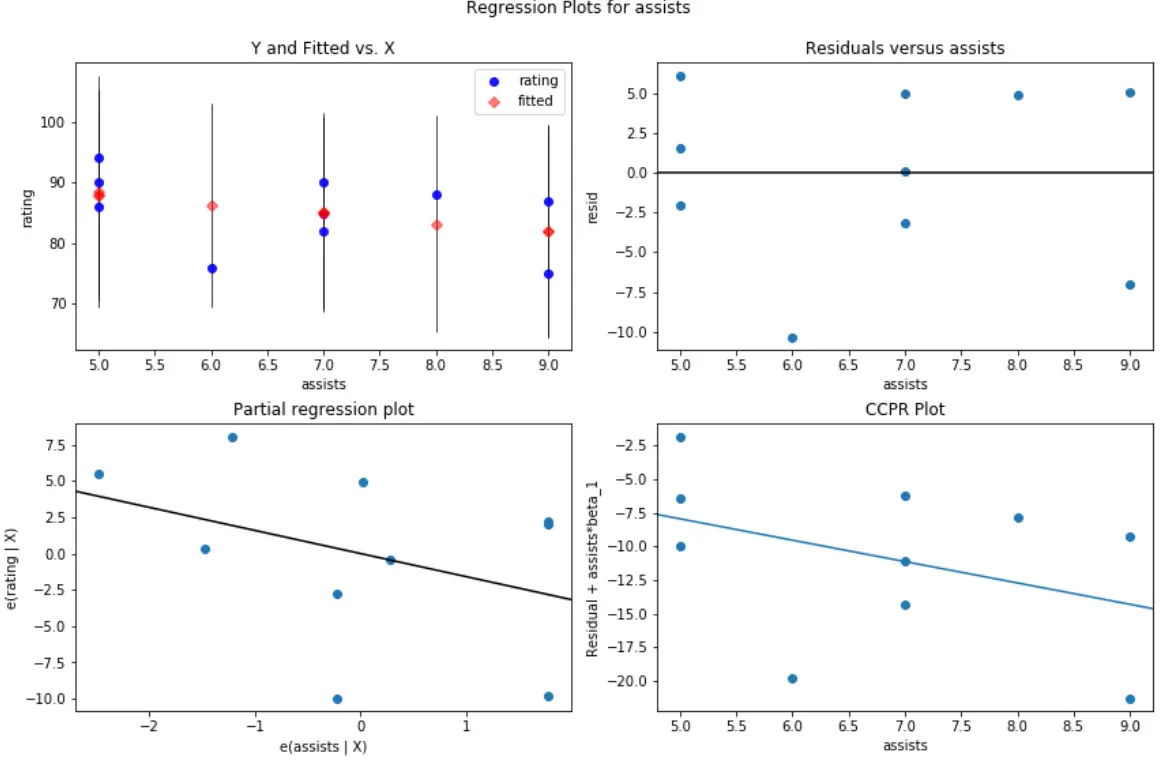
E questo è l’aspetto del grafico residui/predittore per i rimbalzi della variabile predittore:

 #create residual vs. predictor plot for 'assists'
fig = plt.figure(figsize=(12,8))
fig = sm.graphics.plot_regress_exog(model, ' rebounds ', fig=fig)

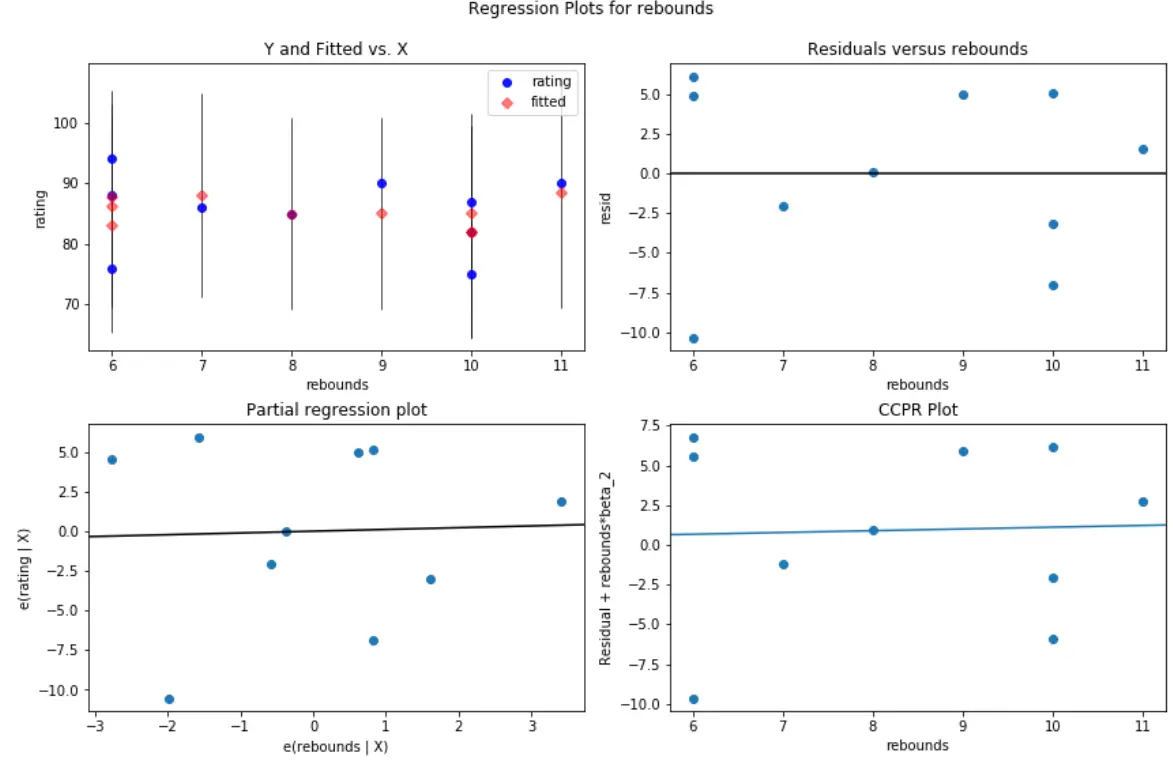
In entrambi i grafici, i residui sembrano essere sparsi in modo casuale attorno allo zero, indicando che l’eteroschedasticità non è un problema con nessuna delle variabili predittive del modello.