Cosa si spiega con la varianza? (definizione & #038; esempio)

La varianza spiegata (a volte chiamata “variazione spiegata”) si riferisce alla varianza della variabile di risposta in un modello che può essere spiegata dalle variabili predittive del modello.

Maggiore è la varianza spiegata di un modello, maggiore è la variazione nei dati che il modello è in grado di spiegare.

La varianza spiegata appare nei risultati di due diversi modelli statistici:

1. ANOVA: utilizzato per confrontare le medie di tre o più gruppi indipendenti.

2. Regressione: utilizzata per quantificare la relazione tra una o più variabili predittive e una variabile di risposta.

Gli esempi seguenti mostrano come interpretare la varianza residua in ciascuno di questi metodi.

Nota : l’opposto della varianza spiegata è chiamato varianza residua .

Varianza spiegata nei modelli ANOVA

Ogni volta che adattiamo un modello ANOVA (“analisi della varianza”), ci ritroviamo con una tabella ANOVA simile alla seguente:

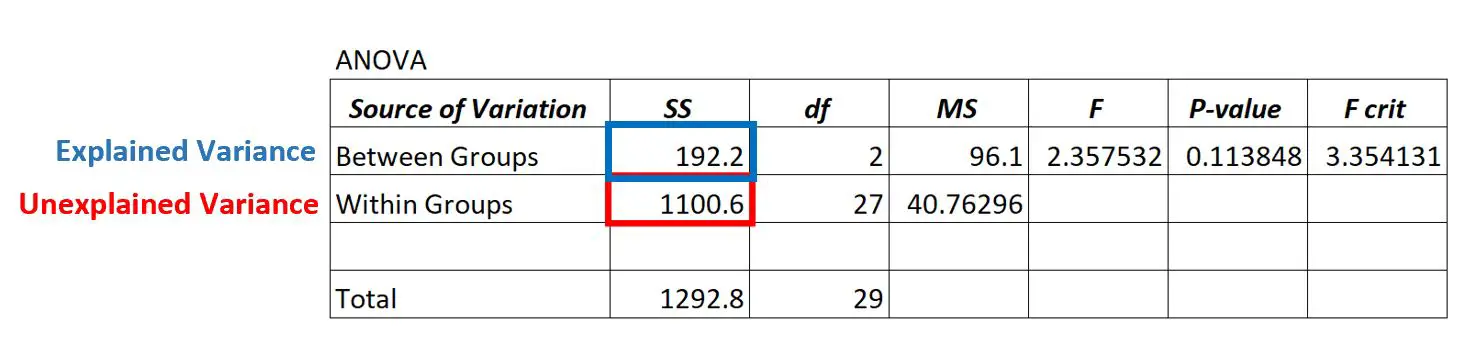
La varianza spiegata si trova nella colonna SS (“somma dei quadrati”) per la variazione tra gruppi .

Nel modello ANOVA sopra, vediamo che la varianza spiegata è 192,2.

Per determinare se questa varianza spiegata è “elevata”, possiamo calcolare la somma media dei quadrati all’interno dei gruppi e la somma media dei quadrati tra i gruppi e trovare il rapporto tra i due, che fornisce il valore F complessivo nella tabella ANOVA.

• F = MS _entra / MS _entra
• F = 96,1/40,76296
• F = 2.357

Il valore F nella tabella ANOVA sopra è 2,357 e il valore p corrispondente è 0,113848.

Poiché questo valore p non è inferiore a α = 0,05, non abbiamo prove sufficienti per rifiutare l’ipotesi nulla di ANOVA .

Ciò significa che non abbiamo prove sufficienti per affermare che la differenza media tra i gruppi che stiamo confrontando sia significativamente diversa.

Questo ci dice che la varianza spiegata nel modello ANOVA è piccola rispetto alla varianza non spiegata.

Varianza spiegata nei modelli di regressione

In un modello di regressione, la varianza spiegata è riassunta come R quadrato , spesso scritto ^R2 .

Questo valore rappresenta la proporzione della varianza nella variabile di risposta che può essere spiegata dalle variabili predittive nel modello.

Il valore di R al quadrato può variare da 0 a dove:

• Un valore pari a 0 indica che la variabile di risposta non può essere spiegata affatto dalle variabili predittive.
• Un valore pari a 1 indica che la variabile di risposta può essere perfettamente spiegata senza errori dalle variabili predittive.

Quando adattiamo un modello di regressione, di solito otteniamo un risultato simile al seguente:

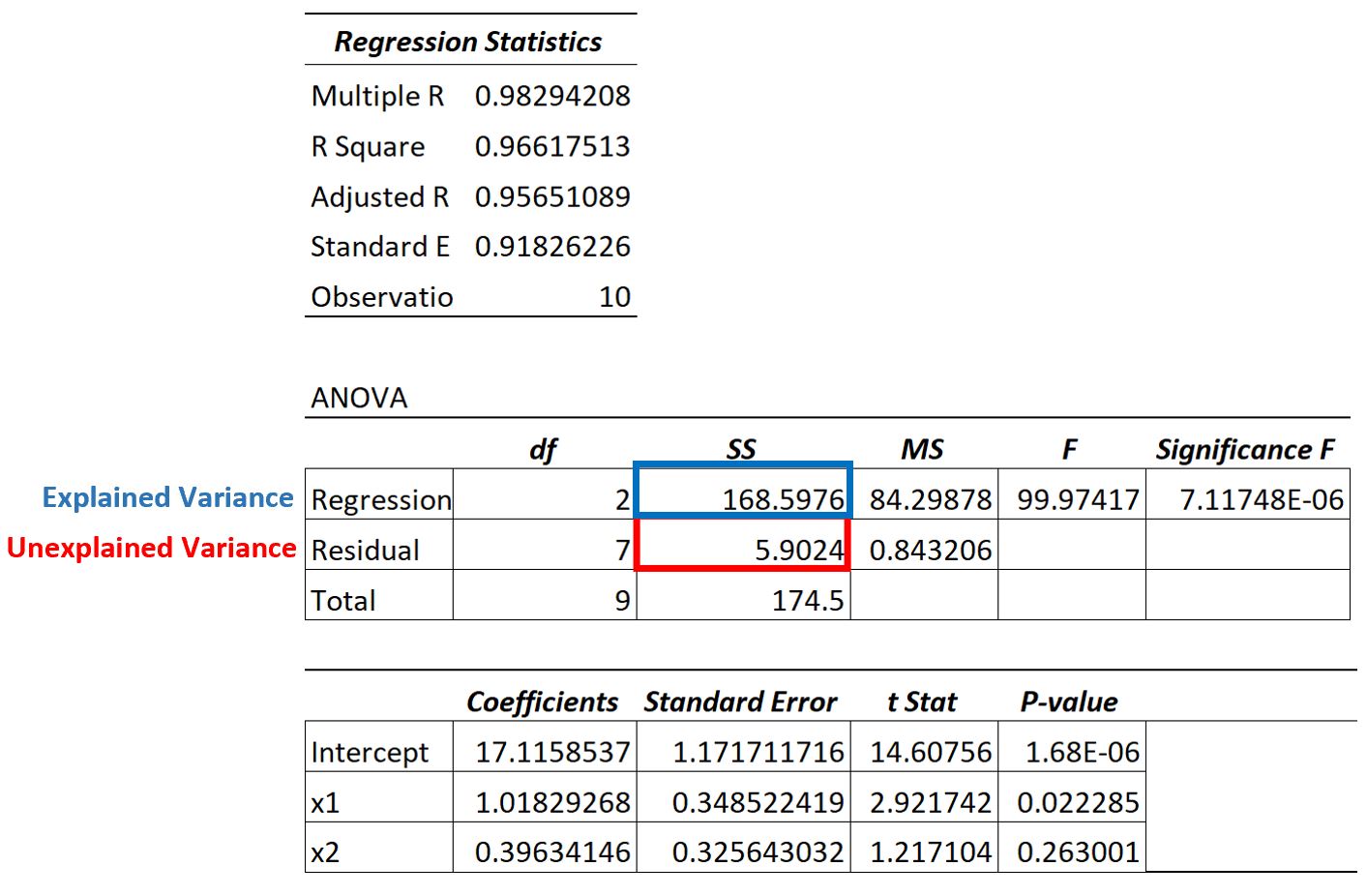
Possiamo vedere che la varianza spiegata è 168,5976 e la varianza totale è 174,5 .

Utilizzando questi valori, possiamo calcolare il valore R quadrato per questo modello di regressione come segue:

• R quadrato: Regressione SS / Totale SS
• R al quadrato: 168,5976 / 174,5
• R al quadrato: 0,966

Poiché il valore R quadrato di questo modello è vicino a 1, ciò ci dice che la varianza spiegata nel modello è estremamente elevata.

In altre parole, il modello è in grado di fare un buon lavoro utilizzando le variabili predittive per spiegare la variazione nella variabile di risposta.

Correlato: Qual è un buon valore R quadrato?