Come applicare il teorema di chebyshev in excel

Il teorema di Chebyshev afferma che per qualsiasi numero k maggiore di 1, almeno 1 – 1/k ² dei valori dei dati in qualsiasi distribuzione addestrata si trova entro k deviazioni standard dalla media.

Ad esempio, per qualsiasi distribuzione sagomata, almeno 1 – 1/3 ² = 88,89% dei valori nella distribuzione rientreranno entro 3 deviazioni standard dalla media.

Questo tutorial illustra diversi esempi di applicazione del teorema di Chebyshev in Excel.

Esempio 1: utilizzare il teorema di Chebyshev per determinare quale percentuale di valori sarà compresa tra 30 e 70 per un set di dati con una media di 50 e una deviazione standard di 10.

Innanzitutto, determina il valore di k. Possiamo farlo determinando quante deviazioni standard sono comprese tra 30 e 70 dalla media:

(30 – media) / deviazione standard = (30 – 50) / 10 = -20 / 10 = -2

(70 – media) / deviazione standard = (70 – 50) / 10 = 20 / 10 = 2

I valori 30 e 70 sono rispettivamente 2 deviazioni standard sotto e sopra la media. Quindi, k = 2 .

Possiamo quindi utilizzare la seguente formula in Excel per trovare la percentuale minima di valori che rientrano in 2 deviazioni standard della media per questo set di dati:

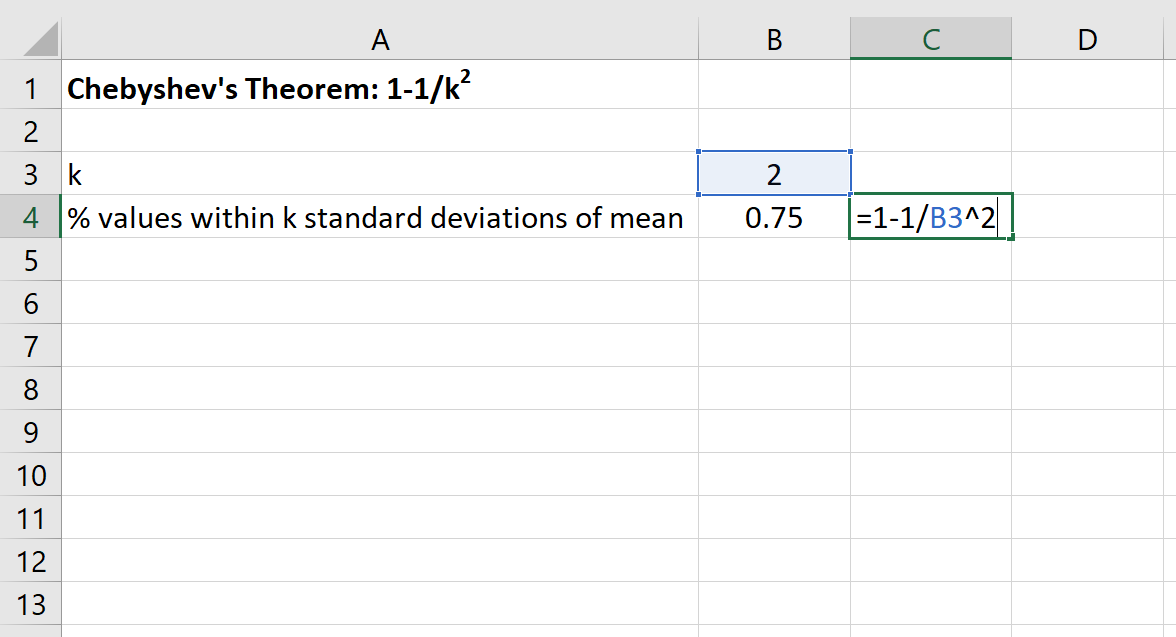
La percentuale di valori compresi tra 30 e 70 per questo set di dati sarà almeno del 75% .

Esempio 2: utilizzare il teorema di Chebyshev per determinare quale percentuale di valori sarà compresa tra 20 e 50 per un set di dati con una media di 35 e una deviazione standard di 5.

Innanzitutto, determina il valore di k. Possiamo farlo determinando quante deviazioni standard sono comprese tra 20 e 50 dalla media:

(20 – media) / deviazione standard = (20 – 35) / 5 = -15 / 5 = -3

(50 – media) / deviazione standard = (50 – 35) / 5 = 15 / 5 = 3

I valori 20 e 50 sono rispettivamente 3 deviazioni standard sotto e sopra la media. Quindi, k = 3 .

Possiamo quindi utilizzare la seguente formula in Excel per trovare la percentuale minima di valori che rientrano nelle 3 deviazioni standard della media per questo set di dati:

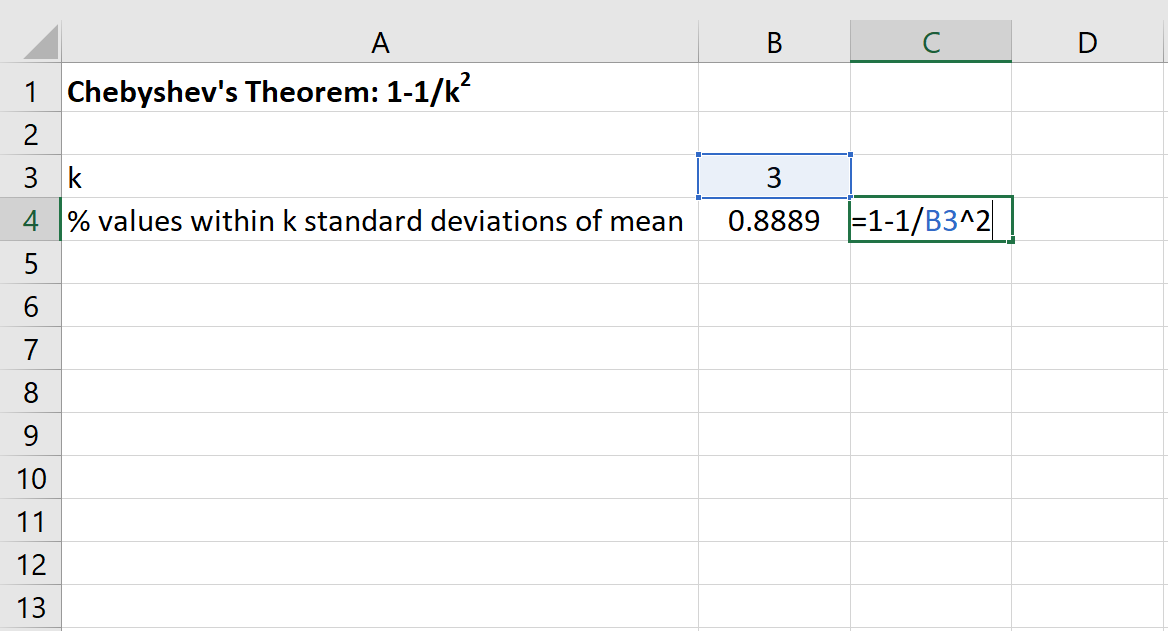
La percentuale di valori compresi tra 20 e 50 per questo set di dati sarà almeno dell’88,89% .

Esempio 3: utilizzare il teorema di Chebyshev per determinare quale percentuale di valori sarà compresa tra 80 e 120 per un set di dati con una media di 100 e una deviazione standard di 5.

Innanzitutto, determina il valore di k. Possiamo farlo determinando quante deviazioni standard sono comprese tra 80 e 120 dalla media:

(80 – media) / deviazione standard = (80 – 100) / 5 = -20 / 5 = -4

(120 – media) / deviazione standard = (120 – 100) / 5 = 20 / 5 = 4

I valori 80 e 120 sono rispettivamente 4 deviazioni standard sotto e sopra la media. Quindi, k = 4 .

Possiamo quindi utilizzare la seguente formula in Excel per trovare la percentuale minima di valori che rientrano nelle 4 deviazioni standard della media per questo set di dati:

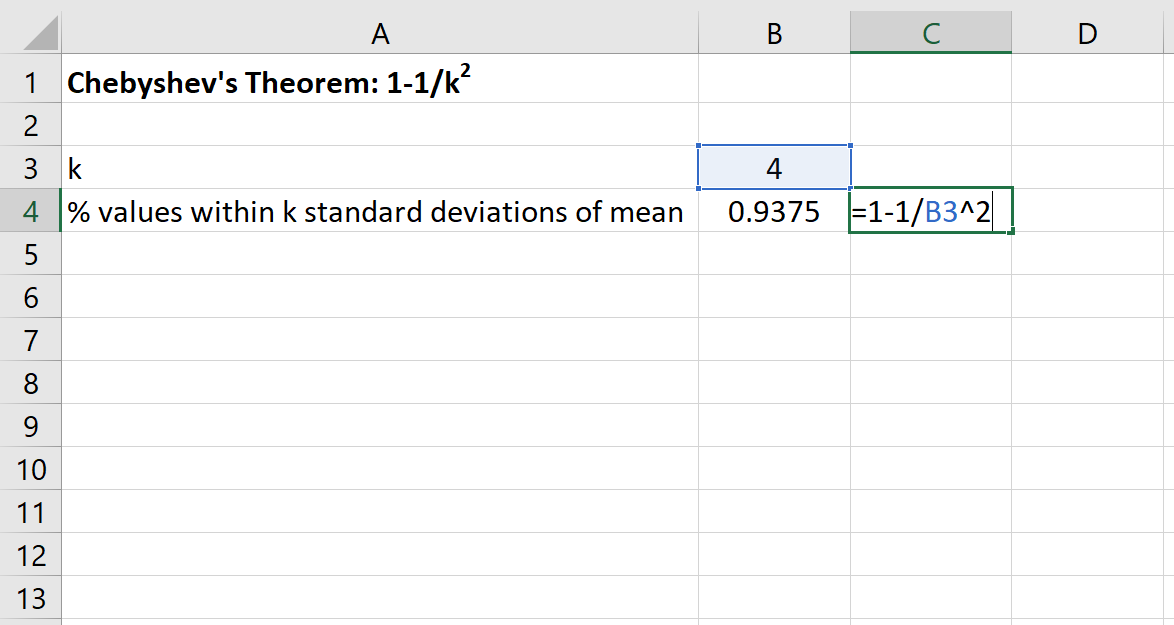
La percentuale di valori compresi tra 80 e 120 per questo set di dati sarà almeno del 93,75% .