Perché la media è importante nelle statistiche?

La media di un set di dati rappresenta il valore medio del set di dati. Viene calcolato come segue:

Media = Σx _i /n

Oro:

• Σ: Un simbolo che significa “somma”
• x _i : l’ ^iesima osservazione in un set di dati
• n: il numero totale di osservazioni nel set di dati

Ad esempio, supponiamo di avere il seguente set di dati con 11 osservazioni:

Set di dati: 3, 4, 4, 6, 7, 8, 12, 13, 15, 16, 17

La media del set di dati viene calcolata come segue:

Media = (3+4+4+6+7+8+12+13+15+16+17) / 11 = 9,54

Nelle statistiche, la media è importante per i seguenti motivi:

1. La media ci dà un’idea di dove si trova il “centro” di un set di dati.

2. A causa del modo in cui viene calcolata, la media contiene informazioni provenienti da ciascuna osservazione in un set di dati.

L’esempio seguente illustra questi due motivi.

Esempio: calcolare la media di un insieme di dati

Supponiamo di avere un set di dati contenente i prezzi di vendita di 10.000 case diverse in una determinata città.

Invece di guardare migliaia di righe di dati grezzi , possiamo calcolare il valore medio per comprendere rapidamente il prezzo medio di vendita delle case in quella città.

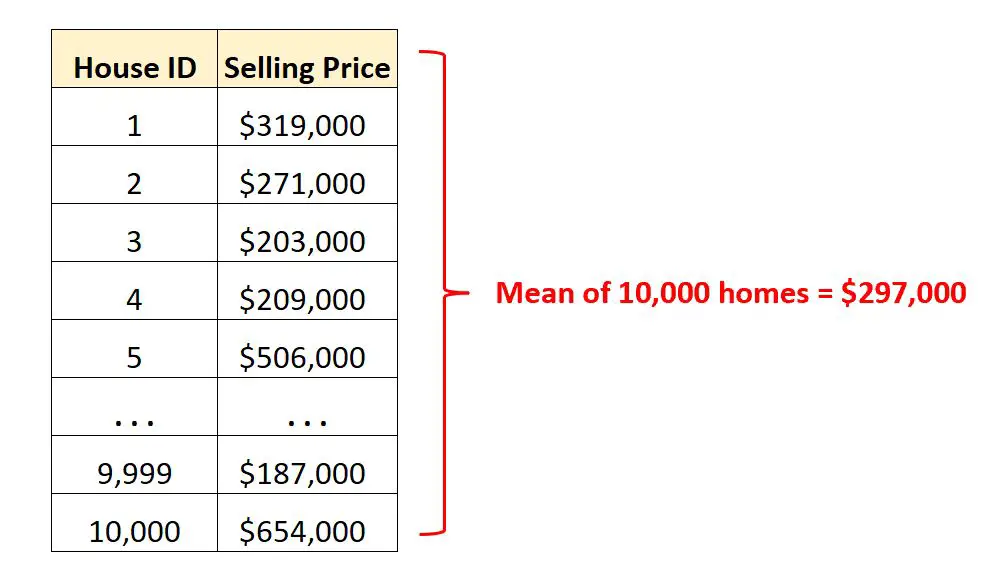
Sapere che il prezzo medio di vendita è di 297.000 dollari ci dà un’idea del prezzo di vendita di una casa “tipica” in questa città.

Questo singolo valore della media è molto più semplice da interpretare rispetto a tutte le righe di dati grezzi.

E poiché per calcolare la media è stato utilizzato il prezzo di vendita di ogni casa, potremmo moltiplicare il prezzo di vendita medio per il numero totale di case per trovare il prezzo di vendita totale di tutte le case in quella città:

• Prezzo di vendita totale di tutte le case = Prezzo di vendita medio * Numero di case
• Prezzo di vendita totale di tutte le case = $ 297.000 * 10.000
• Prezzo di vendita totale di tutte le case = $ 2.970.000.000

Possiamo vedere che il prezzo di vendita totale di tutte le case in questa città è di 2,97 miliardi di dollari.

Quando utilizzare la media

Quando analizziamo i set di dati, spesso vogliamo capire dove si trova il valore centrale.

In statistica, esistono due parametri comuni che utilizziamo per misurare il centro di un set di dati:

• Media : il valore medio in un insieme di dati
• Mediana : il valore mediano in un set di dati

La media è il modo più comune per misurare il centro di un set di dati, ma in realtà può essere fuorviante nelle seguenti situazioni:

• Quando la distribuzione è asimmetrica .
• Quando la distribuzione contiene valori anomali .

Per illustrare ciò, si considerino i due esempi seguenti.

Esempio 1: calcolo della media di una distribuzione asimmetrica

Considera la seguente distribuzione degli stipendi per i residenti di una determinata città:

I salari elevati sul lato destro della distribuzione allontanano la media dal centro della distribuzione.

Pertanto, la mediana riflette meglio la retribuzione “tipica” di un residente rispetto alla media, perché la distribuzione è sbilanciata verso destra.

In questo particolare esempio, lo stipendio medio è di $ 47.000 mentre lo stipendio medio è di $ 32.000.

Pertanto, la mediana è molto più rappresentativa dello stipendio tipico di quella città.

Esempio 2: calcolo della media in presenza di valori anomali

Considera il seguente grafico che mostra la metratura delle case in una determinata strada:

La media è fortemente influenzata da alcune case estremamente grandi, mentre la mediana non lo è.

Possiamo vedere che la mediana fa un lavoro migliore nel catturare la metratura “tipica” di una casa su quella strada rispetto alla media, perché non è influenzata da valori anomali.

Riepilogo

Ecco un breve riassunto dei principali punti salienti di questo articolo:

• La media rappresenta il valore medio in un insieme di dati.
• La media è importante perché ci dà un’idea di dove si trova il valore centrale in un set di dati.
• La media è importante anche perché contiene informazioni su ciascuna osservazione in un set di dati.
• La media può essere fuorviante quando un set di dati è distorto o contiene valori anomali. In questi scenari, la mediana dà un’idea più precisa di dove si trova il “centro” di un set di dati.

Risorse addizionali

Le seguenti esercitazioni forniscono informazioni aggiuntive su altre statistiche descrittive:

Perché la mediana è importante nelle statistiche?
Perché la deviazione standard è importante nelle statistiche?
Quando utilizzare la media rispetto alla mediana