Perché la modalità è importante nelle statistiche?

La modalità rappresenta il valore che appare più spesso in un set di dati.

Un set di dati non può avere modalità (se non ci sono valori ripetuti), una modalità o più modalità.

Ad esempio, la modalità nel set di dati seguente è 19:

Set di dati: 3, 4, 11, 15, 19 , 19, 19 , 22 , 22, 23, 23, 26

Questo è il valore che appare più spesso.

Nelle statistiche, la modalità è importante per i seguenti motivi:

Motivo 1 : questo ci consente di sapere quali valori in un set di dati sono i più comuni.

Motivo 2 : è utile per trovare il valore più frequente nei dati categoriali quando non è possibile calcolare la media e la mediana.

Motivo 3 : Ci dà un’idea di dove si trova il “centro” di un set di dati, anche se la mediana e la media sono più comunemente usate (come vedremo più avanti in questo articolo).

Gli esempi seguenti illustrano nella pratica ciascuno di questi motivi.

Motivo 1: la modalità ci dice quale valore è più comune

Supponiamo di avere un set di dati di 100.000 righe contenente i prezzi di vendita delle case negli Stati Uniti:

Supponiamo di utilizzare software statistico (come Excel , R , Python , ecc.) per calcolare la modalità di questo set di dati e scoprire che esistono tre modalità:

• $ 280.000
• $ 300.000
• $ 305.000

Questo ci dà immediatamente un’idea dei prezzi delle case più comuni nel set di dati.

Calcolare la modalità migliaia è anche molto più veloce che guardare righe di dati e cercare di identificare quali prezzi delle case si verificano più spesso.

Motivo 2: la modalità ricerca il valore più comune nei dati categoriali

Supponiamo di avere un set di dati di 1.000 righe che ci dice il colore dell’auto posseduta dagli individui in un determinato quartiere:

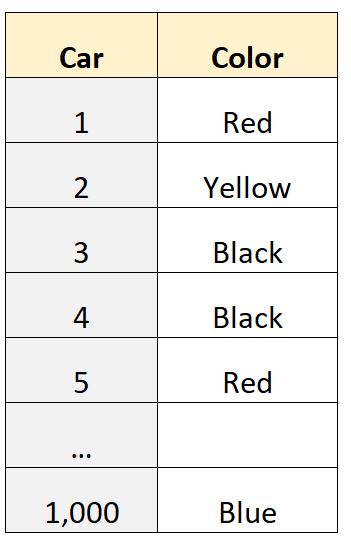
La variabile “colore” è una variabile categoriale , ciò significa che i valori appartengono a categorie (“rosso”, “giallo”, “nero”, ecc.) e quindi non possiamo calcolare un valore quantitativo come la media o la mediana .

Tuttavia, possiamo calcolare la moda perché rappresenta semplicemente il valore più comune nel set di dati.

Ad esempio, potremmo utilizzare un software statistico per determinare che la modalità di questo set di dati è “nera”, il che ci dice che il colore dell’auto più comune in questo set di dati è il nero.

Motivo 3: la modalità ci dà un’idea di dove si trova il centro di un set di dati

La moda è anche considerata una misura della tendenza centrale , nel senso che può darci un’idea di dove si trova il “centro” dell’insieme di dati.

Ad esempio, supponiamo di avere il seguente set di dati che mostra i punteggi degli esami di 20 studenti diversi in una classe:

La modalità risulta essere 82 : questo è il punteggio dell’esame più comune. Ciò risulta anche essere una buona indicazione di dove si trova il valore del punteggio di revisione “principale” in questo set di dati.

Tuttavia, supponiamo di avere invece il seguente set di dati dei risultati degli esami:

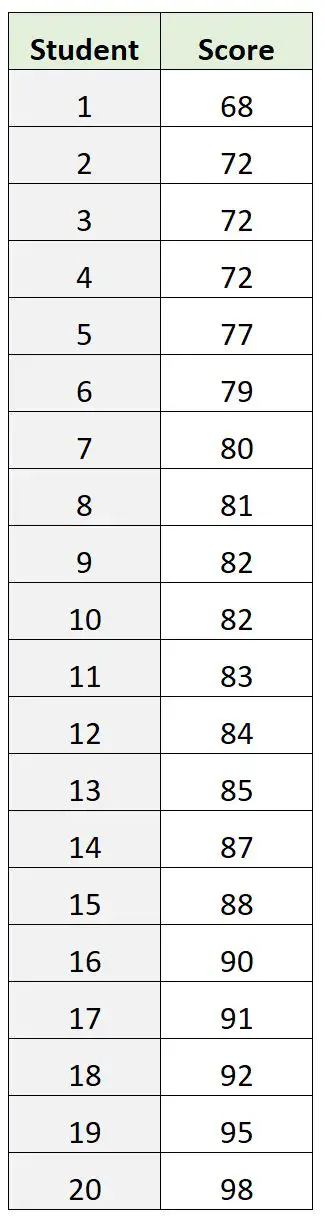
In questo set di dati, 72 è il punteggio dell’esame di moda. Tuttavia, ciò risulta essere una scarsa indicazione di dove si trova il punteggio “fondamentale” dell’esame.

Il punteggio medio dell’esame è 82,9 e il punteggio medio dell’esame è 82,5 , entrambi i quali ci danno un’idea migliore di dove si trova il valore “centrale” in relazione alla moda.

Riepilogo

Ecco un breve riassunto dei punti principali trattati in questo articolo:

• La modalità rappresenta i valori che appaiono più spesso in un set di dati.
• La moda ci indica il valore più comune nei dati categoriali quando la media e la mediana non possono essere utilizzate.
• La modalità ci dà un’idea di dove si trova il “centro” di un set di dati, ma può essere fuorviante se confrontata con la media o la mediana.

Risorse addizionali

Le seguenti esercitazioni forniscono informazioni aggiuntive su media, mediana e moda nelle statistiche:

Perché la media è importante nelle statistiche?
Perché la mediana è importante nelle statistiche?
Esempi concreti: utilizzo della media, della mediana e della moda
Quando utilizzare la media vs. Mediana: con esempi