Come interpretare i rapporti di probabilità

In statistica la probabilità si riferisce alla probabilità che un evento si verifichi. Viene calcolato come segue:

PROBABILITÀ:

P(evento) = (# risultati desiderabili) / (# risultati possibili)

Ad esempio, supponiamo di avere quattro palline rosse e una verde in un sacchetto. Se chiudi gli occhi e selezioni una pallina a caso, la probabilità che tu scelga una pallina verde viene calcolata come segue:

P(verde) = 1/5 = 0,2 .

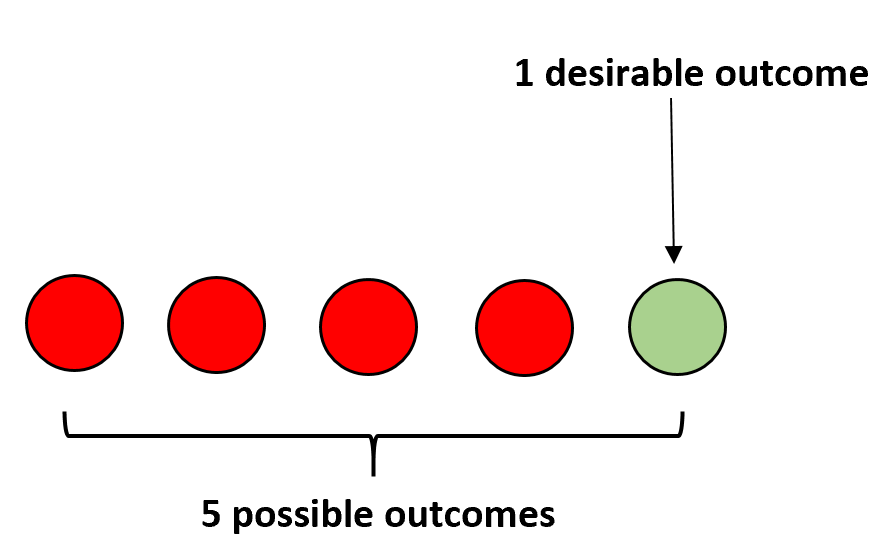
Le probabilità che un evento si verifichi possono essere calcolate come segue:

PROBABILITÀ:

Possibilità (evento) = P (l’evento si verifica) / 1-P (l’evento si verifica)

Ad esempio, le probabilità di tirare una pallina verde sono (0,2)/1-(0,2) = 0,2/0,8 = 0,25 .

L’ odds ratio è il rapporto tra due probabilità.

RAPPORTO FORTUNA:

Rapporto quote = Quote dell’evento A / Quote dell’evento B

Ad esempio, potremmo calcolare il rapporto di probabilità tra la scelta di una pallina rossa e di una pallina verde.

La probabilità di estrarre una pallina rossa è 4/5 = 0,8 .

Le probabilità di estrarre una pallina rossa sono (0,8) / 1-(0,8) = 0,8 / 0,2 = 4 .

Il rapporto di probabilità per la scelta di una pallina rossa rispetto a una pallina verde viene calcolato come segue:

Quota (rossa) / Quota (verde) = 4 / 0,25 = 16 .

Quindi le probabilità di tirare una palla rossa sono 16 volte maggiori di quelle di sparare una palla verde.

Quando vengono utilizzati i rapporti di probabilità nel mondo reale?

Nel mondo reale, i rapporti di probabilità vengono utilizzati in una varietà di contesti in cui i ricercatori desiderano confrontare le probabilità che si verifichino due eventi. Ecco alcuni esempi.

Esempio n. 1: interpretazione dei rapporti di probabilità

I ricercatori vogliono sapere se un nuovo trattamento migliora le possibilità che un paziente abbia un risultato positivo sulla salute rispetto a un trattamento esistente. La tabella seguente mostra il numero di pazienti che hanno avuto un esito positivo o negativo sulla salute, a seconda del trattamento.

Le probabilità che un paziente abbia un esito positivo con il nuovo trattamento possono essere calcolate come segue:

Probabilità = P(positivo) / 1 – P(positivo) = (50/90) / 1-(50/90) = (50/90) / (40/90) = 1,25

Le probabilità che un paziente abbia un esito positivo con il trattamento esistente possono essere calcolate come segue:

Probabilità = P(positivo) / 1 – P(positivo) = (42/90) / 1-(42/90) = (42/90) / (48/90) = 0,875

Pertanto, l’odds ratio di ottenere un risultato positivo con il nuovo trattamento rispetto al trattamento esistente può essere calcolato come segue:

Rapporto probabilità = 1,25 / 0,875 = 1,428 .

Interpretiamo questo nel senso che le probabilità che un paziente abbia un esito positivo utilizzando il nuovo trattamento sono 1,428 volte le probabilità che un paziente abbia un esito positivo utilizzando il trattamento esistente.

In altre parole, con il nuovo trattamento le possibilità di ottenere un risultato positivo aumentano del 42,8% .

Esempio n.2: interpretazione dei rapporti di probabilità

Gli esperti di marketing vogliono sapere se un annuncio induce i clienti ad acquistare un determinato articolo più spesso di un altro annuncio. Quindi mostrano ogni annuncio a 100 persone. La tabella seguente mostra il numero di persone che hanno acquistato l’articolo, in base all’annuncio visto:

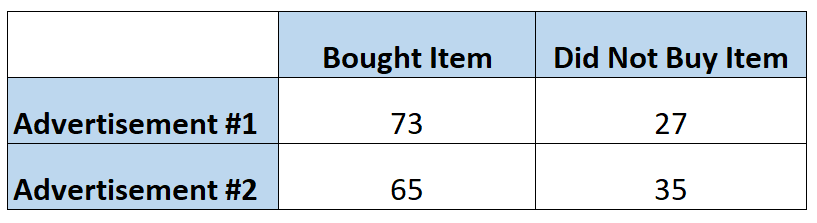
Le probabilità che un individuo acquisti l’articolo dopo aver visto il primo annuncio possono essere calcolate come segue:

Quote = P(comprato) / 1 – P(comprato) = (73/100) / 1-(73/100) = (73/100) / (27/100) = 2.704

Le probabilità che un individuo acquisti l’articolo dopo aver visto il secondo annuncio possono essere calcolate come segue:

Quote = P(comprato) / 1 – P(comprato) = (65/100) / 1-(65/10) = (65/100) / (35/100) = 1.857

Pertanto, il rapporto di probabilità tra un cliente che acquista l’articolo dopo aver visto il primo annuncio e un cliente che lo acquista dopo aver visto il secondo annuncio può essere calcolato come segue:

Rapporto probabilità = 2.704 / 1.857 = 1.456 .

Interpretiamo questo nel senso che le probabilità che un individuo acquisti l’articolo dopo aver visto il primo annuncio sono 1.456 volte le probabilità che un individuo acquisti l’articolo dopo aver visto il secondo annuncio.

In altre parole, grazie alla prima inserzione le possibilità di acquistare l’oggetto aumentano del 45,6% .

Risorse addizionali

Come calcolare il rapporto quote e il rischio relativo in Excel
Come interpretare un rapporto di probabilità inferiore a 1
Come interpretare il rischio relativo