Guida completa: come interpretare i risultati anova in sas

Un’ANOVA unidirezionale viene utilizzata per determinare se esiste o meno una differenza statisticamente significativa tra le medie di tre o più gruppi indipendenti.

L’esempio seguente mostra come interpretare i risultati di un’ANOVA unidirezionale in SAS.

Esempio: interpretare i risultati ANOVA in SAS

Supponiamo che un ricercatore recluti 30 studenti per partecipare a uno studio. Agli studenti viene assegnato in modo casuale uno dei tre metodi di studio per prepararsi a un esame.

Di seguito sono riportati i risultati degli esami per ciascuno studente:

Possiamo utilizzare il seguente codice per creare questo set di dati in SAS:

 /*create dataset*/
data my_data;
    input Method $Score;
    datalines ;
At 78
At 81
At 82
At 82
At 85
At 88
At 88
At 90
B 81
B 83
B 83
B85
B 86
B 88
B90
B91
C 84
C 88
C 88
C 89
C 90
C 93
C 95
C 98
;
run ;

Successivamente, utilizzeremo proc ANOVA per eseguire l’ANOVA unidirezionale:

 /*perform one-way ANOVA*/
proc ANOVA data =my_data;
    classMethod ;
    modelScore = Method;
    means Method / tukey cldiff ;
run ;

Nota : abbiamo utilizzato la dichiarazione di media insieme alle opzioni tukey e cldiff per specificare che un test post-hoc di Tukey dovrebbe essere eseguito (con intervalli di confidenza) se il valore p complessivo dell’ANOVA unidirezionale è statisticamente significativo.

Innanzitutto, esamineremo la tabella ANOVA nel risultato:

Ecco come interpretare ciascun valore nell’output:

Modello DF: i gradi di libertà per il metodo variabile. Questo viene calcolato come #gruppi -1. In questo caso c’erano 3 diversi metodi di studio, quindi questo valore è: 3-1 = 2 .

Errore DF: i gradi di libertà dei residui. Questo viene calcolato come #osservazioni totali – #gruppi. In questo caso c’erano 24 osservazioni e 3 gruppi, quindi questo valore è: 24-3 = 21 .

Totale corretto : la somma del modello DF e dell’errore DF. Questo valore è 2 + 21 = 23 .

Modello della somma dei quadrati: la somma dei quadrati associati al metodo della variabile. Questo valore è 175.583 .

Errore somma dei quadrati: somma dei quadrati associati ai residui o “errori”. Questo valore è 350,25 .

Totale della somma dei quadrati corretta : la somma del modello SS e dell’errore SS. Questo valore è 525.833 .

Modello dei quadrati medi: somma media dei quadrati associati al metodo . Questo viene calcolato come modello SS / modello DF, ovvero 175.583 / 2 = 87.79 .

Errore quadratico medio: somma media dei quadrati associati ai residui. Questo viene calcolato come Errore SS/Errore DF, ovvero 350,25 / 21 = 16,68 .

Valore F: la statistica F complessiva del modello ANOVA. Questo viene calcolato come errore quadratico medio/errore quadratico medio del modello o 87,79/16,68 = 5,26 .

Pr >F: il valore p associato alla statistica F con numeratore df = 2 e denominatore df = 21. In questo caso, il valore p è 0,0140 .

Il valore più importante nell’insieme dei risultati è il valore p, perché ci dice se c’è una differenza significativa nei valori medi tra i tre gruppi.

Ricordiamo che un’ANOVA unidirezionale utilizza le seguenti ipotesi nulle e alternative:

• H ₀ (ipotesi nulla): tutte le medie dei gruppi sono uguali.
• H _A (ipotesi alternativa): almeno una media del gruppo è diversa dalle altre.

Poiché il valore p nella nostra tabella ANOVA (0,0140) è inferiore a 0,05, rifiutiamo l’ipotesi nulla.

Ciò significa che abbiamo prove sufficienti per affermare che il punteggio medio dell’esame non è uguale nei tre metodi di studio.

Per determinare esattamente quali medie di gruppo sono diverse, dobbiamo fare riferimento alla tabella dei risultati finali che mostra i risultati dei test post-hoc di Tukey:

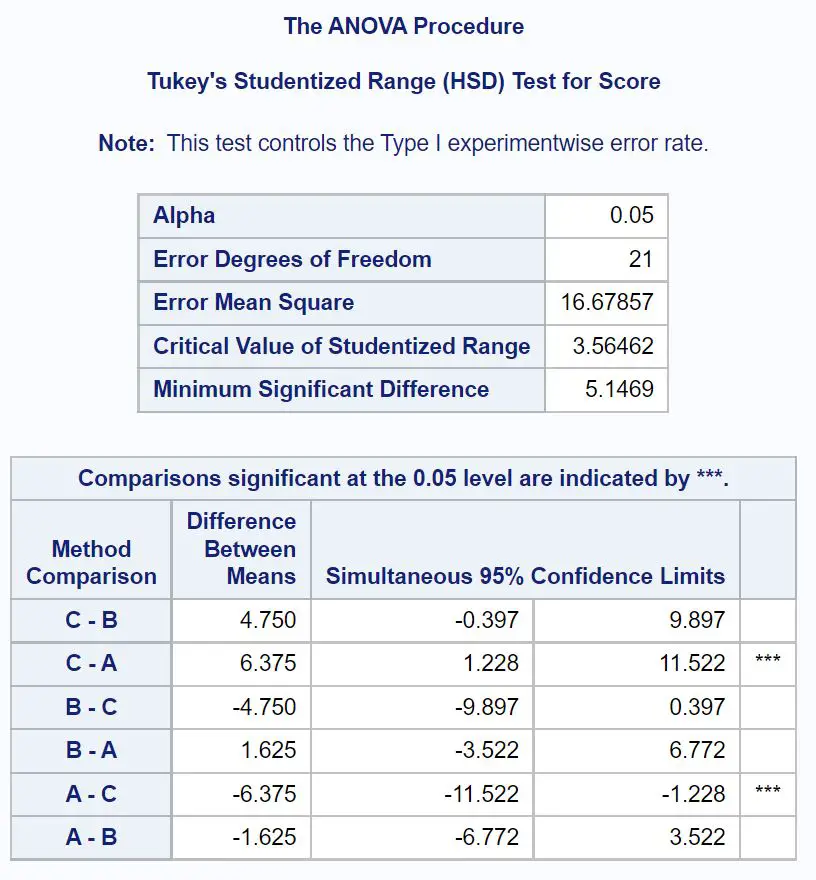
Per scoprire quali medie di gruppo sono diverse, dobbiamo vedere quali confronti a coppie hanno stelle ( *** ) accanto a loro.

La tabella mostra che esiste una differenza statisticamente significativa nei punteggi medi degli esami tra il Gruppo A e il Gruppo C.

Nello specifico, la differenza media nei punteggi degli esami tra il Gruppo C e il Gruppo A è 6.375 .

L’intervallo di confidenza al 95% per la differenza media è [1,228, 11,522] .

Non ci sono differenze statisticamente significative tra le medie degli altri gruppi.

Risorse addizionali

Le seguenti esercitazioni forniscono informazioni aggiuntive sui modelli ANOVA:

Una guida all’utilizzo dei test post-hoc con ANOVA
Come eseguire ANOVA unidirezionale in SAS
Come eseguire ANOVA bidirezionale in SAS