Guida completa: come interpretare i risultati anova in excel

Un’ANOVA unidirezionale viene utilizzata per determinare se esiste o meno una differenza statisticamente significativa tra le medie di tre o più gruppi indipendenti.

L’esempio seguente fornisce una guida completa su come interpretare i risultati di un’ANOVA unidirezionale in Excel.

Esempio: come interpretare i risultati ANOVA in Excel

Supponiamo che un insegnante chieda a caso a 30 studenti della sua classe di utilizzare uno dei tre metodi di studio per prepararsi a un esame.

Lo screenshot seguente mostra i punteggi degli studenti in base al metodo utilizzato:

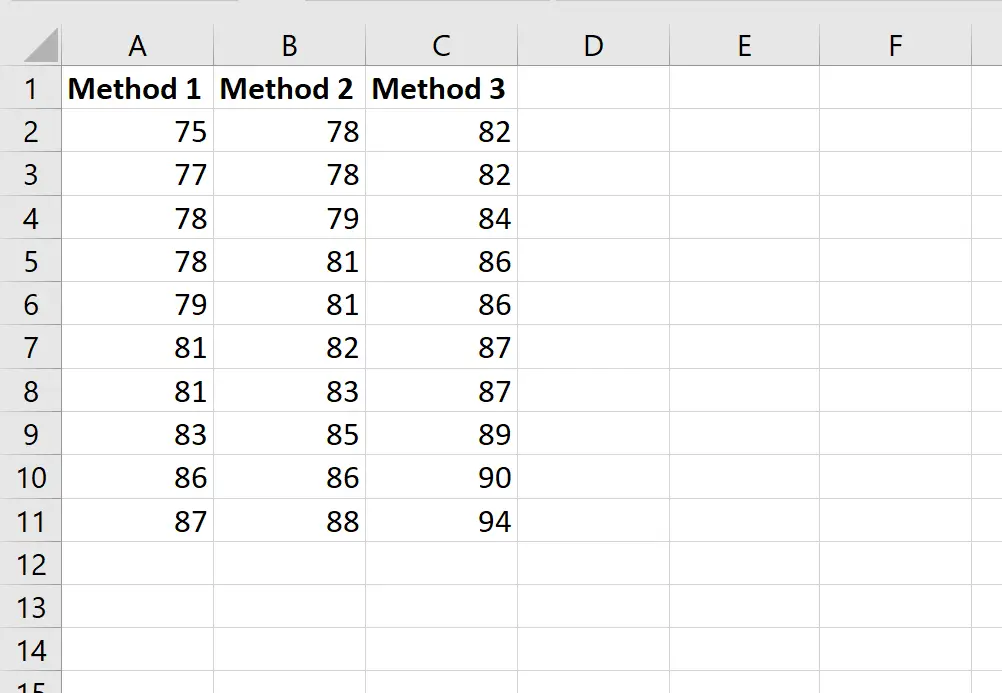
Supponiamo che l’insegnante voglia eseguire un’ANOVA unidirezionale per determinare se i punteggi medi sono gli stessi nei tre gruppi.

Per eseguire un’ANOVA unidirezionale in Excel, fare clic sulla scheda Dati lungo la barra multifunzione superiore, quindi su Analisi dati nel gruppo Analizza .

Se non vedi l’opzione Analisi dati , devi prima caricare il software gratuito Analysis ToolPak .

Dopo aver fatto clic su di esso, verrà visualizzata una nuova finestra. Selezionare Anova: Fattore singolo , quindi fare clic su OK .

Nella nuova finestra che appare, inserisci le seguenti informazioni:

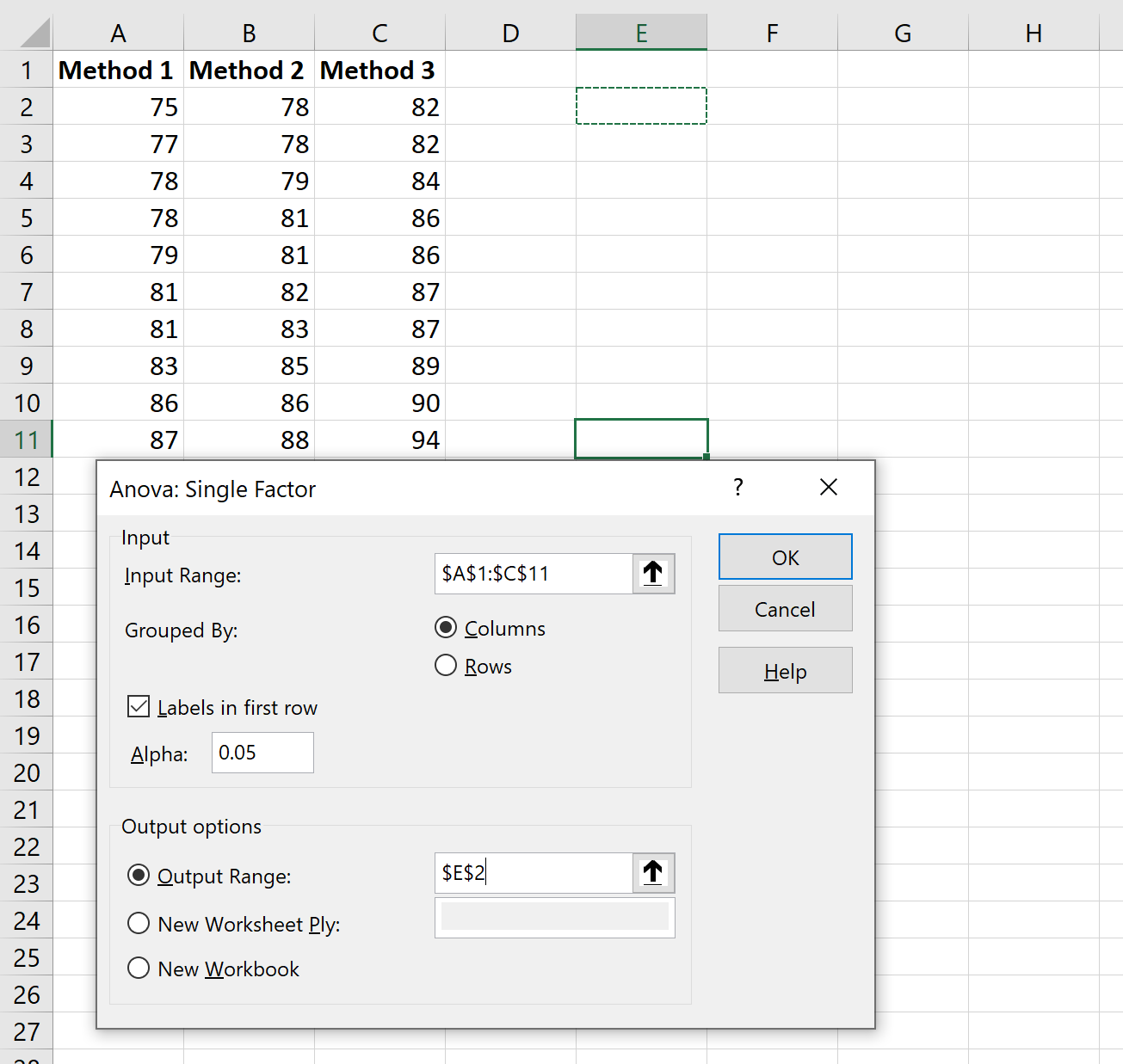
Dopo aver fatto clic su OK , verranno visualizzati i risultati ANOVA unidirezionali:

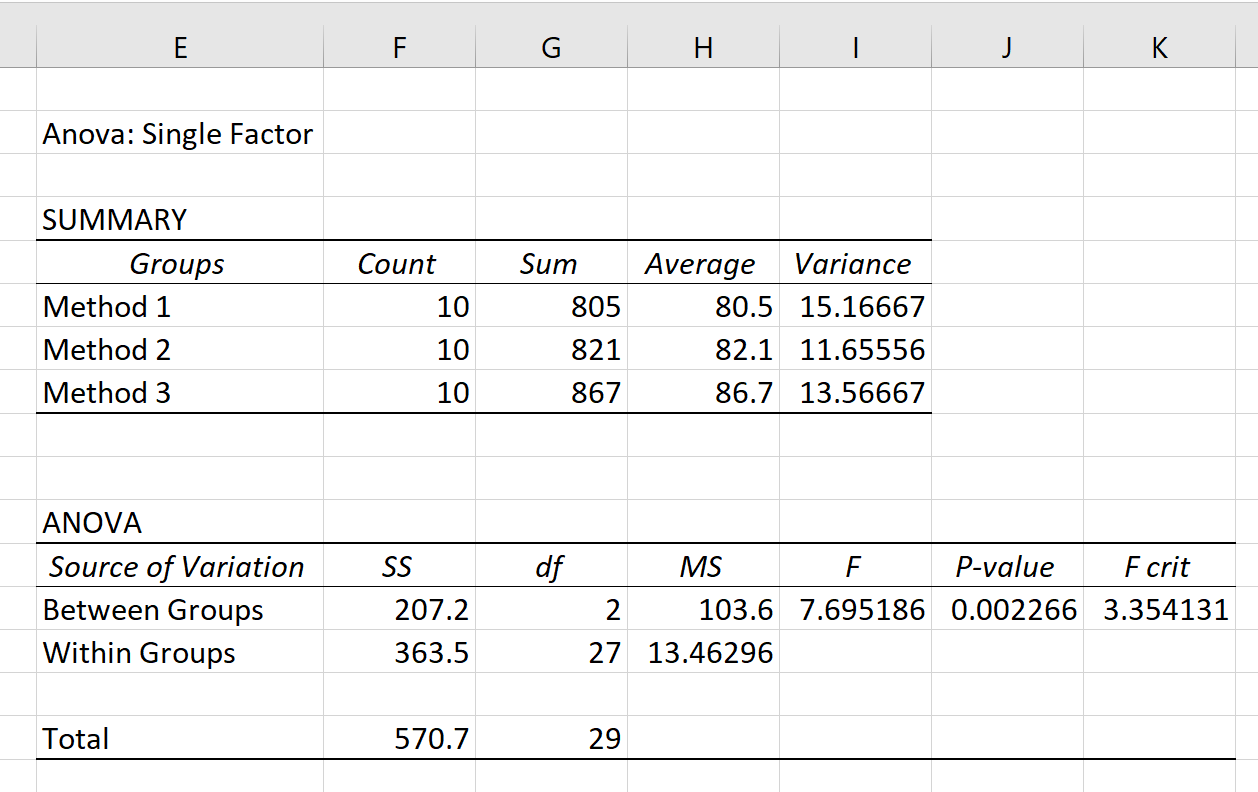
Nel risultato vengono visualizzate due tabelle: SUMMARY e ANOVA .

Ecco come interpretare i valori in ciascuna tabella:

Tabella RIASSUNTIVA :

• Gruppi : nomi dei gruppi
• Conteggio : il numero di osservazioni in ciascun gruppo
• Somma : la somma dei valori di ciascun gruppo
• Media : il valore medio in ciascun gruppo
• Varianza : la varianza dei valori in ciascun gruppo

Questa tabella ci fornisce diverse statistiche riassuntive utili per ciascun gruppo utilizzato nell’ANOVA.

Da questa tabella possiamo vedere che gli studenti che hanno utilizzato il Metodo 3 hanno ottenuto il punteggio medio più alto all’esame (86,7), ma hanno anche avuto la varianza più alta nei punteggi dei test. revisione (13.56667).

Per determinare se le differenze nelle medie dei gruppi sono statisticamente significative, dobbiamo fare riferimento alla tabella ANOVA.

Tabella ANOVA :

• Fonte della variazione : la variazione misurata (tra gruppi o all’interno dei gruppi)
• SS : La somma dei quadrati per ciascuna fonte di variazione
• df : I gradi di libertà, calcolati come #gruppi-1 per df Tra e #osservazioni – #gruppi per df Entro
• MS : la somma media dei quadrati, calcolata in SS/df
• F : il valore F complessivo, calcolato come MS Between / MS Within
• Valore P : il valore p corrispondente al valore F complessivo
• F crit : Il valore critico F che corrisponde a α = 0,05

Il valore più importante in questa tabella è il valore p , che risulta essere 0.002266 .

Ricordiamo che un’ANOVA unidirezionale utilizza le seguenti ipotesi nulle e alternative:

• H ₀ : tutte le medie dei gruppi sono uguali.
• H _A : Non tutte le medie dei gruppi sono uguali.

Poiché il valore p è inferiore a α = 0,05, rifiutiamo l’ipotesi nulla dell’ANOVA unidirezionale e concludiamo che abbiamo prove sufficienti per affermare che tutte le medie dei gruppi non sono uguali.

Ciò significa che non tutti e tre i metodi di studio portano agli stessi voti medi negli esami.

Nota : è anche possibile confrontare il valore F complessivo con il valore F critico per determinare se rifiutare o meno l’ipotesi nulla. In questo caso, poiché il valore complessivo di F è maggiore del valore critico di F, rifiuteremo l’ipotesi nulla. Si noti che l’approccio del valore p e l’approccio del valore F critico porteranno sempre alla stessa conclusione.

Risorse addizionali

I seguenti tutorial spiegano come eseguire diversi ANOVA in Excel:

Come eseguire ANOVA unidirezionale in Excel
Come eseguire un’ANOVA bidirezionale in Excel
Come eseguire ANOVA a misure ripetute in Excel
Come eseguire ANOVA nidificati in Excel