Come interpretare i valori di verosimiglianza (con esempi)

Il valore logaritmico di un modello di regressione è un modo per misurare la bontà di adattamento di un modello. Maggiore è il valore di verosimiglianza, migliore è il modello che si adatta a un set di dati.

Il valore della logaritmo per un dato modello può variare da infinito negativo a infinito positivo. Il valore effettivo della verosimiglianza logaritmica per un dato modello è generalmente privo di significato, ma è utile per confrontare due o più modelli .

In pratica, spesso adattiamo più modelli di regressione a un set di dati e scegliamo il modello con il valore di log-verosimiglianza più alto come modello che meglio si adatta ai dati.

L’esempio seguente mostra come interpretare nella pratica i valori di verosimiglianza per diversi modelli di regressione.

Esempio: interpretazione dei valori di verosimiglianza

Supponiamo di avere il seguente set di dati che mostra il numero di camere da letto, il numero di bagni e i prezzi di vendita di 20 case diverse in un particolare quartiere:

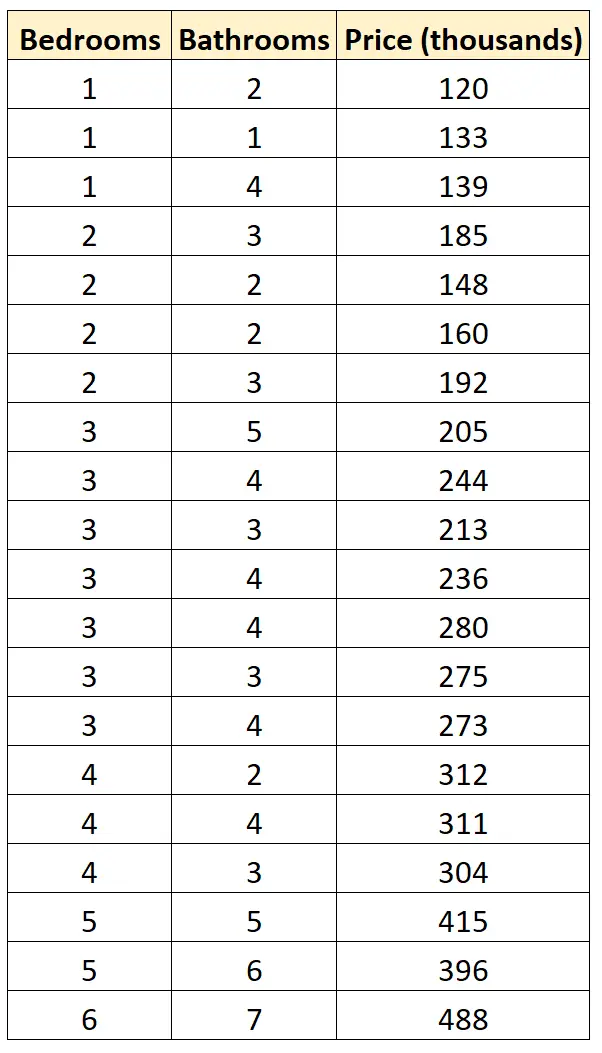
Supponiamo di voler adattare i seguenti due modelli di regressione e determinare quale fornisce l’adattamento migliore ai dati:

Modello 1 : Prezzo = β ₀ + β ₁ (numero di camere)

Modello 2 : Prezzo = β ₀ + β ₁ (numero di bagni)

Il codice seguente mostra come adattare ciascun modello di regressione e calcolare il valore di verosimiglianza di ciascun modello in R:

 #define data
df <- data. frame (beds=c(1, 1, 1, 2, 2, 2, 2, 3, 3, 3,
                        3, 3, 3, 3, 4, 4, 4, 5, 5, 6),
                 baths=c(2, 1, 4, 3, 2, 2, 3, 5, 4, 3,
                         4, 4, 3, 4, 2, 4, 3, 5, 6, 7),
                 price=c(120, 133, 139, 185, 148, 160, 192, 205, 244, 213,
                         236, 280, 275, 273, 312, 311, 304, 415, 396, 488))

#fitmodels
model1 <- lm(price~beds, data=df)
model2 <- lm(price~baths, data=df)

#calculate log-likelihood value of each model
logLik(model1)

'log Lik.' -91.04219 (df=3)

logLik(model2)

'log Lik.' -111.7511 (df=3)

Il primo modello ha un valore di verosimiglianza logaritmica più elevato ( -91.04 ) rispetto al secondo modello ( -111.75 ), il che significa che il primo modello fornisce un migliore adattamento ai dati.

Precauzioni per l’utilizzo dei valori di verosimiglianza

Quando si calcolano i valori di verosimiglianza logaritmica, è importante notare che l’aggiunta di ulteriori variabili predittive a un modello aumenterà quasi sempre il valore di verosimiglianza logaritmica, anche se le variabili predittive aggiuntive non sono statisticamente significative.

Ciò significa che dovresti confrontare i valori di verosimiglianza tra due modelli di regressione solo se ciascun modello ha lo stesso numero di variabili predittive.

Per confrontare modelli con numeri diversi di variabili predittive, è possibile eseguire un test del rapporto di verosimiglianza per confrontare la bontà dell’adattamento di due modelli di regressione nidificati.

Risorse addizionali

Come utilizzare la funzione lm() per adattare modelli lineari in R
Come eseguire un test del rapporto di verosimiglianza in R