Come calcolare un intervallo di confidenza per il rischio relativo

Il rischio relativo viene spesso calcolato quando si analizza una tabella 2×2, che assume il seguente formato:

Il rischio relativo ci dice la probabilità che un evento si verifichi in un gruppo di trattamento rispetto alla probabilità che un evento si verifichi in un gruppo di controllo.

Viene calcolato come segue:

• Rischio relativo = [A/(A+B)] / [C/(C+D)]

Possiamo quindi utilizzare la seguente formula per calcolare un intervallo di confidenza per il rischio relativo (RR):

• CI inferiore al 95% = e ^{ln(RR) – 1,96√ 1/a + 1/c – 1/(a+b) – 1/(c+d)}
• CI maggiore del 95% = e ^{ln(RR) + 1,96√ 1/a + 1/c – 1/(a+b) – 1/(c+d)}

L’esempio seguente mostra come calcolare nella pratica un rischio relativo e un corrispondente intervallo di confidenza.

Esempio: calcolo di un intervallo di confidenza per il rischio relativo

Supponiamo che un allenatore di basket utilizzi un nuovo programma di allenamento per vedere se aumenta il numero di giocatori che possono superare un determinato test di abilità, rispetto a un vecchio programma di allenamento.

L’allenatore recluta 50 giocatori per utilizzare ciascun programma. La tabella seguente mostra il numero di giocatori che hanno superato e fallito il test di abilità, in base al programma utilizzato:

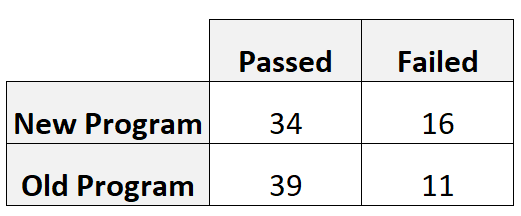
Possiamo calcolare il rischio relativo come segue:

• Rischio relativo = [A/(A+B)] / [C/(C+D)]
• Rischio relativo = [34/(34+16)] / [39/(39+11)]
• Rischio relativo = 0,8718

Interpretiamo questo nel senso che la probabilità che un giocatore superi il test utilizzando il nuovo programma è solo 0,8718 volte la probabilità che un giocatore superi il test utilizzando il vecchio programma.

In altre parole, la probabilità che un giocatore superi il test viene effettivamente ridotta grazie all’uso del nuovo programma.

Possiamo quindi utilizzare le seguenti formule per calcolare l’intervallo di confidenza al 95% per il rischio relativo:

• CI inferiore al 95% = e ^{ln(.8718) – 1,96√ (1/34 + 1/39 – 1/(34+16) – 1/(39+11)} = 0,686
• CI maggiore del 95% = e ^{ln(.8718) + 1,96√ (1/34 + 1/39 + 1/(34+16) – 1/(39+11)} = 1,109

Pertanto, l’intervallo di confidenza al 95% per il rischio relativo è [0,686, 1,109] .

Siamo sicuri al 95% che il vero rischio relativo tra il nuovo e il vecchio programma di allenamento sia contenuto entro questo intervallo.

Poiché questo intervallo di confidenza contiene il valore 1, non è statisticamente significativo.

Ciò dovrebbe avere senso se si considera quanto segue:

• Un rischio relativo maggiore di 1 significherebbe che la probabilità che un giocatore superi il test utilizzando il nuovo programma è maggiore della probabilità che un giocatore superi il test utilizzando il vecchio programma.
• Un rischio relativo inferiore a 1 significherebbe che la probabilità che un giocatore superi il test utilizzando il nuovo programma è inferiore alla probabilità che un giocatore superi il test utilizzando il vecchio programma.

Quindi, poiché il nostro intervallo di confidenza al 95% per il rischio relativo contiene il valore 1, ciò significa che la probabilità che un giocatore superi il test di abilità utilizzando il nuovo programma può o meno essere maggiore della probabilità che lo stesso giocatore superi il test utilizzando il nuovo programma. nuovo programma. vecchio programma.

Risorse addizionali

I seguenti tutorial forniscono ulteriori informazioni sui rapporti di probabilità e sul rischio relativo:

Come interpretare i rapporti di probabilità
Come interpretare il rischio relativo
Come calcolare il rapporto probabilità e il rischio relativo in Excel