Come calcolare un intervallo di confidenza di poisson (passo dopo passo)

La distribuzione di Poisson è una distribuzione di probabilità utilizzata per modellare la probabilità che un certo numero di eventi si verifichino durante un intervallo di tempo fisso quando è noto che gli eventi si verificano in modo indipendente e con un tasso medio costante.

Sebbene sia utile conoscere il numero medio di occorrenze di un processo di Poisson, può essere ancora più utile avere un intervallo di confidenza attorno al numero medio di occorrenze.

Ad esempio, supponiamo di raccogliere dati presso un call center in un giorno casuale e di vedere che il numero medio di chiamate all’ora è 15.

Poiché abbiamo raccolto i dati solo per un giorno, non possiamo essere sicuri che il call center riceva in media 15 chiamate all’ora durante tutto l’anno.

Tuttavia, possiamo utilizzare la seguente formula per calcolare un intervallo di confidenza per il numero medio di chiamate all’ora:

Formula dell’intervallo di confidenza di Poisson

Intervallo di confidenza = [0,5*X ² _{2N, α/2} , 0,5*X ² _{2(N+1), 1-α/2} ]

Oro:

• X ² : Valore critico del chi quadrato
• N: il numero di eventi osservati
• α: il livello di significatività

Il seguente esempio passo passo illustra come calcolare nella pratica un intervallo di confidenza di Poisson al 95%.

Passaggio 1: contare gli eventi osservati

Supponiamo di calcolare che il numero medio di chiamate all’ora in un call center sia 15. Quindi, N = 15 .

E poiché stiamo calcolando un intervallo di confidenza del 95%, utilizzeremo α = 0,05 nei calcoli seguenti.

Passaggio 2: trovare il limite inferiore dell’intervallo di confidenza

Il limite inferiore dell’intervallo di confidenza viene calcolato come segue:

• Limite inferiore = 0,5*X ² _{2N, α/2}
• Limite inferiore = 0,5*X ² _{2(15), 0,975}
• Limite inferiore = 0,5*X ² _{30, 0,975}
• Limite inferiore = 0,5*16,791
• Limite inferiore = 8,40

Nota: abbiamo utilizzato il calcolatore del valore critico del chi quadrato per calcolare X ² _{30, 0,975} .

Passaggio 3: trovare il limite superiore dell’intervallo di confidenza

Il limite superiore dell’intervallo di confidenza viene calcolato come segue:

• Limite superiore = 0,5*X ² _{2(N+1), 1-α/2}
• Limite superiore = 0,5*X ² _{2(15+1), 0,025}
• Limite superiore = 0,5*X ² _{32, 0,025}
• Limite superiore = 0,5*49,48
• Limite superiore = 24,74

Nota: abbiamo utilizzato il calcolatore del valore critico del chi quadrato per calcolare X ² _32.0.025 .

Passaggio 4: trovare l’intervallo di confidenza

Utilizzando i limiti inferiore e superiore calcolati in precedenza, il nostro intervallo di confidenza di Poisson al 95% risulta essere:

• IC al 95% = [8,40, 24,74]

Ciò significa che siamo sicuri al 95% che l’effettivo numero medio di chiamate orarie che il call center riceve è compreso tra 8,40 chiamate e 24,74 chiamate.

Bonus: calcolatore dell’intervallo di confidenza dei pesci

Sentiti libero di utilizzare questo calcolatore dell’intervallo di confidenza di Poisson per calcolare automaticamente un intervallo di confidenza di Poisson.

Ad esempio, ecco come utilizzare questa calcolatrice per trovare l’intervallo di confidenza di Poisson che abbiamo appena calcolato manualmente:

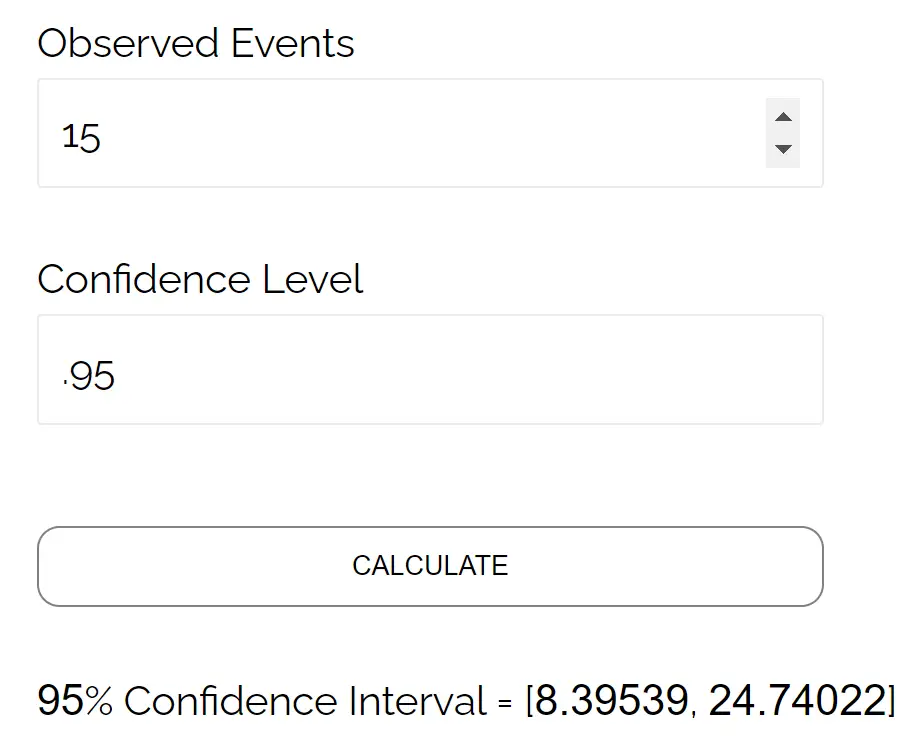
Tieni presente che i risultati corrispondono all’intervallo di confidenza che abbiamo calcolato manualmente.