Come costruire un intervallo di previsione in excel

In statistica, la regressione lineare semplice è una tecnica che possiamo utilizzare per quantificare la relazione tra una variabile predittrice, x, e una variabile di risposta, y.

Quando eseguiamo una regressione lineare semplice, otteniamo una “linea di miglior adattamento” che descrive la relazione tra x e y, che può essere scritta come:

ŷ = b ₀ + b ₁ x

Oro:

• ŷ è il valore previsto della variabile di risposta
• b ₀ è l’intercetta y
• b ₁ è il coefficiente di regressione
• x è il valore della variabile predittore

A volte vogliamo usare questa linea di miglior adattamento per costruire un intervallo di previsione per un dato valore di x ₀ , che è un intervallo attorno al valore previsto ŷ ₀ tale che ci sia una probabilità del 95% che il vero valore di y nella popolazione corrispondente a x ₀ è incluso in questo intervallo.

La formula per calcolare l’intervallo di previsione per un dato valore x ₀ è scritta:

ŷ ₀ +/- t _α/2,df=n-2 * se

Oro:

se = S _yx √(1 + 1/n + (x ₀ – x ) ² /SS _x )

La formula può sembrare un po’ intimidatoria, ma in realtà è semplice da calcolare in Excel. Successivamente vedremo un esempio dell’utilizzo di questa formula per calcolare un intervallo di previsione per un determinato valore in Excel.

Esempio: come costruire un intervallo di previsione in Excel

Il seguente set di dati mostra il numero di ore studiate e il punteggio dell’esame ottenuto da 15 studenti diversi:

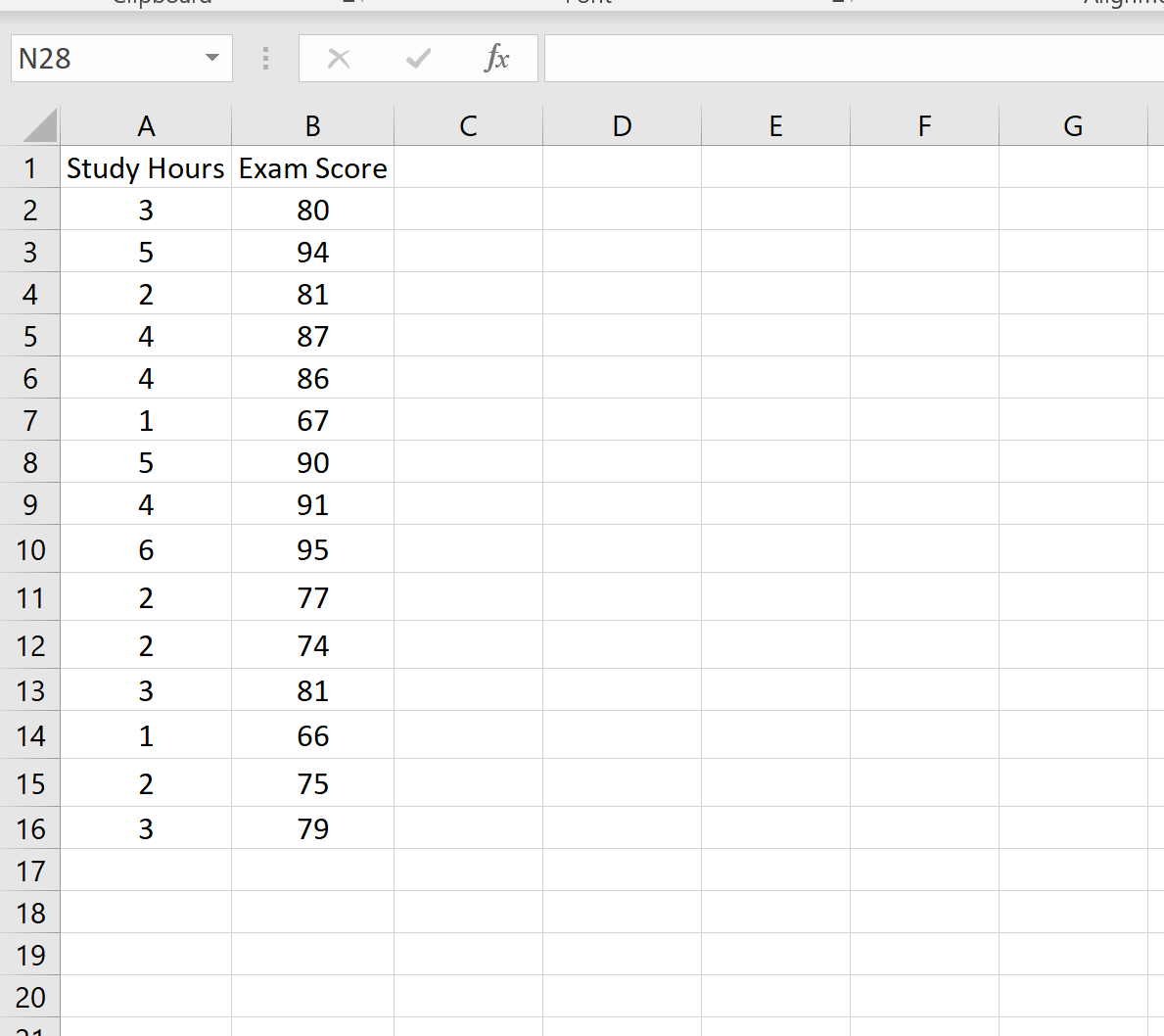
Supponiamo di voler creare un intervallo di previsione del 95% per il valore x ₀ = 3. Cioè, vogliamo creare un intervallo tale che ci sia una probabilità del 95% che il punteggio dell’esame rientri in questo intervallo per uno studente che studia per 3 ore.

Lo screenshot seguente mostra come calcolare tutti i valori necessari per ottenere questo intervallo di previsione.

Nota: le formule nella colonna F mostrano come sono stati calcolati i valori nella colonna E.

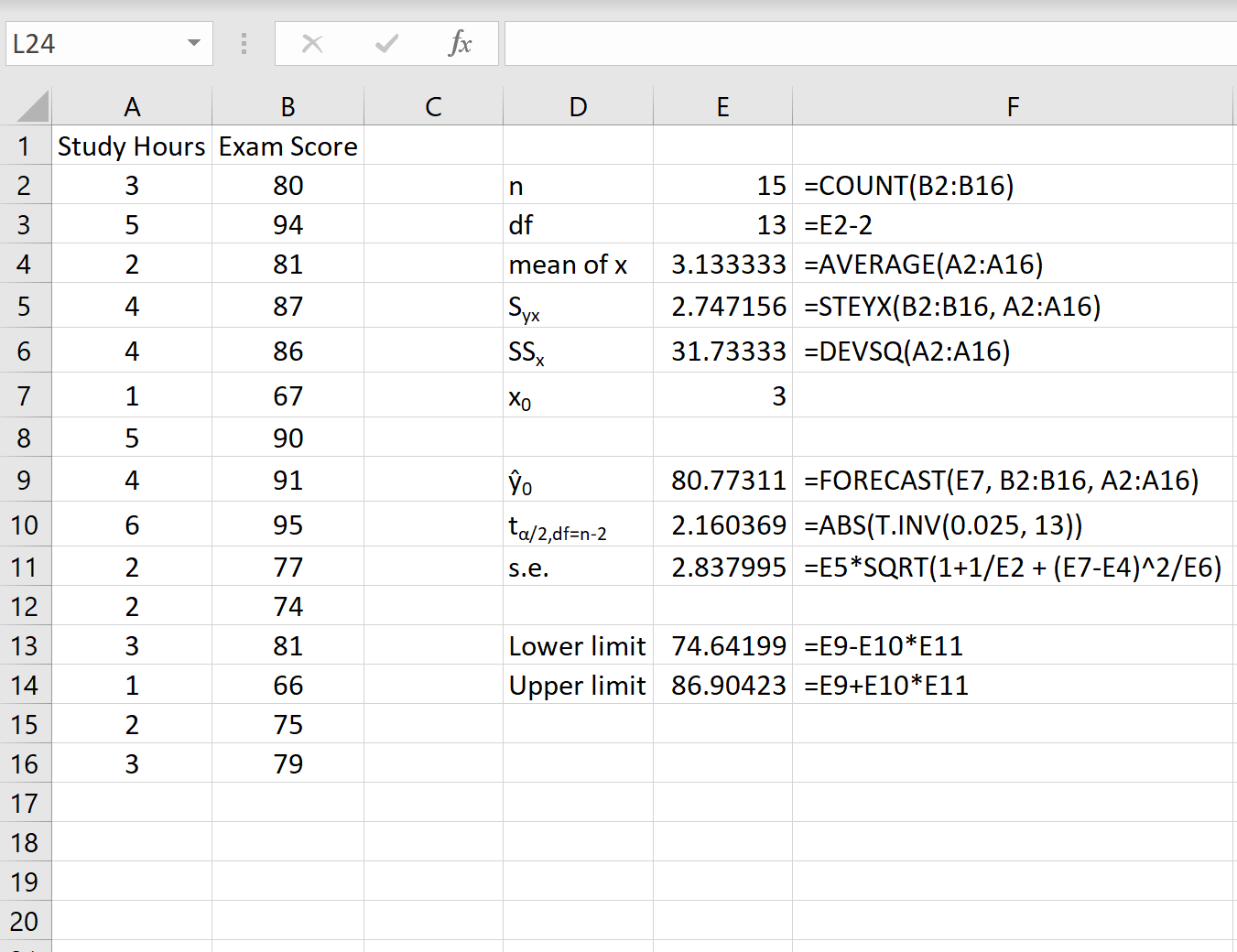
L’intervallo di previsione del 95% per un valore di x ₀ = 3 è (74,64, 86,90) . Cioè prevediamo con una probabilità del 95% che uno studente che studia per 3 ore otterrà un punteggio compreso tra 74,64 e 86,90.

Alcune note sui calcoli utilizzati:

• Per calcolare il valore t-critico di t _α/2,df=n-2, abbiamo utilizzato α/2 = 0,05/2 = 0,25 poiché volevamo un intervallo di previsione del 95%. Si noti che intervalli di previsione più elevati (ad esempio, intervallo di previsione del 99%) porteranno a intervalli più ampi. Al contrario, un intervallo di previsione più piccolo (ad esempio un intervallo di previsione del 90%) porterà ad un intervallo di previsione più ristretto.
• Abbiamo utilizzato la formula =PRECAST() per ottenere il valore previsto per ŷ ₀ ma la formula =FORECAST.LINEAR() restituirà esattamente lo stesso valore.