Classifica (statistica)

In questo articolo spieghiamo cos’è l’intervallo nelle statistiche e come viene calcolato. Troverai un esercizio risolto sulla portata di un dataset e, infine, ti mostreremo a cosa serve e quando va utilizzato.

Cos’è l’intervallo nelle statistiche?

In statistica, l’intervallo è una misura di dispersione che indica la differenza tra il valore massimo e il valore minimo dei dati di un campione. Pertanto, per calcolare l’entità di una popolazione o di un campione statistico, è necessario sottrarre il valore massimo dal valore minimo.

Ad esempio, se il valore massimo di un set di dati è 9 e il valore minimo è 2, l’intervallo di questo campione statistico è 7 (9-2=7).

L’intervallo statistico è anche chiamato estensione o intervallo di misurazione.

Pertanto, l’intervallo è una misura della dispersione con varianza, deviazione standard (o deviazione standard), deviazione media e coefficiente di variazione.

Come calcolare l’intervallo nelle statistiche

L’intervallo di un campione viene calcolato sottraendo i valori estremi dei dati statistici del campione, ovvero l’intervallo di un campione è uguale al valore massimo di tutti i dati meno il valore minimo .

Pertanto, la formula per calcolare l’intervallo statistico di un set di dati è:

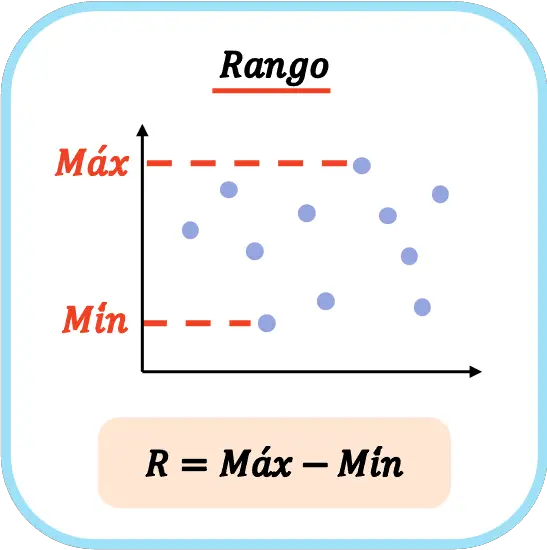
Nelle statistiche, il simbolo della R maiuscola viene spesso utilizzato per denotare l’estensione di una serie di dati.

Calcolare l’intervallo di un set di dati è quindi abbastanza semplice, poiché è sufficiente determinare la differenza tra i valori estremi. L’unica cosa a cui devi prestare attenzione è ottenere i dati massimi e minimi corretti e non dimenticare alcun numero.

Intervallo di esempio (statistica)

Dopo aver visto la definizione di intervallo nelle statistiche, di seguito è riportato un esempio pratico in cui puoi vedere come viene ottenuto l’intervallo di un set di dati.

• Un’azienda vuole analizzare statisticamente le vendite realizzate dal suo prodotto di punta negli ultimi vent’anni. Per fare ciò, ti chiedono di calcolare diverse misure statistiche, inclusa la classifica. Se le vendite del prodotto sono quelle mostrate nella tabella seguente, qual è l’intervallo di questo set di dati?

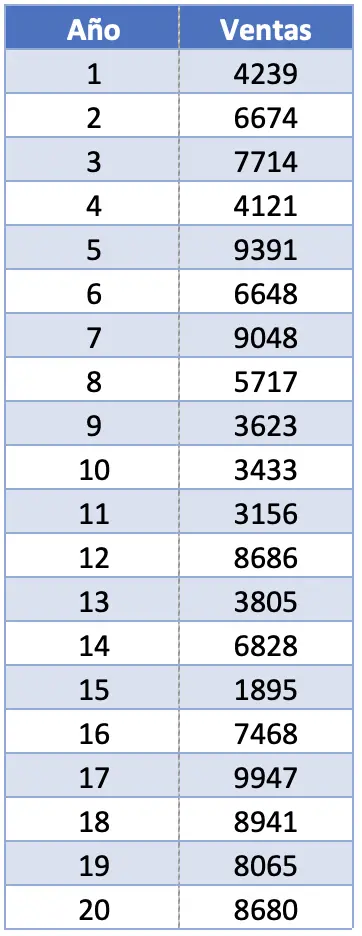
In questo esercizio abbiamo 20 osservazioni. In realtà, il numero totale di osservazioni non fa alcuna differenza nel calcolo dell’entità di un campione, perché a noi interessa solo il valore più grande e quello più piccolo.

Dobbiamo quindi utilizzare la formula vista sopra per trovare l’entità di questo campione statistico.

Il valore massimo dell’intervallo è 9947 unità vendute e il valore minimo è 1895. Pertanto, dobbiamo sottrarre questi due valori per trovare l’intervallo del set di dati:

Ciò significa che la variazione massima delle vendite negli ultimi anni è di 8.052 unità. Di seguito puoi vedere graficamente tutti i dati dell’esercizio insieme al suo range statistico, il grafico probabilmente ti aiuterà a capire il significato del range.

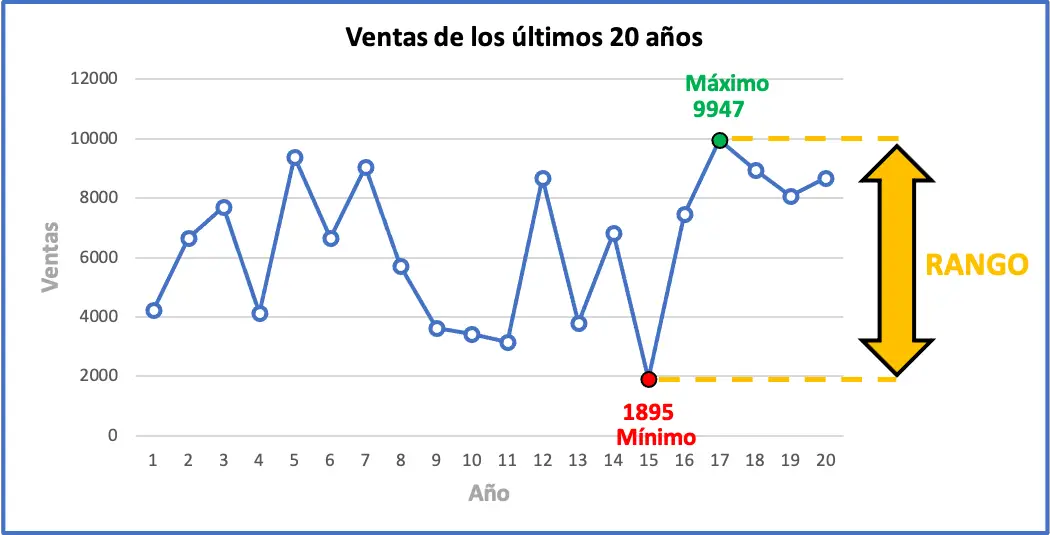
A cosa serve l’intervallo statistico?

Per finire di comprendere la nozione di estensione in statistica, vedremo a cosa serve e come interpretare questa misura di dispersione.

Nelle statistiche, l’intervallo mostra la differenza tra il valore massimo e il valore minimo di un set di dati. Pertanto, l’intervallo è una misura utilizzata per indicare la dispersione totale di un set di dati .

Quando conosci il valore dell’intervallo di un set di dati, conosci la differenza massima tra due osservazioni qualsiasi in quel set, quindi puoi avere un’idea se i dati sono sparsi o vicini tra loro. In generale è vantaggioso che il range sia il più minimo possibile, perché questo significa che c’è poca dispersione e quindi i calcoli saranno più accurati.

Ad esempio, il range può essere una misura che permette il confronto tra due campioni diversi, perché permette di farsi un’idea delle dispersioni dei campioni.

Tuttavia, occorre prestare cautela nell’interpretazione dell’intervallo statistico, poiché può essere fuorviante. È possibile che un set di dati abbia effettivamente una dispersione molto bassa, ma se è presente un valore anomalo all’interno del campione, l’intervallo sarà molto ampio e quindi non rifletterà adeguatamente la dispersione del campione.

Inoltre, non è la stessa cosa che un campione i cui valori sono dell’ordine delle decine abbia un rango pari a 5, come un campione i cui valori sono dell’ordine delle migliaia abbia lo stesso rango. Logicamente, anche se entrambi gli intervalli hanno lo stesso numero, il primo campione è molto più disperso del secondo.

In conclusione, il range è una misura statistica utile per analizzare la dispersione di un set di dati, ma per interpretare correttamente i dati è necessario calcolare anche altre metriche.