Le tre ipotesi formulate in un t test per dati appaiati

Un test t per campioni accoppiati viene utilizzato per confrontare le medie di due campioni quando ciascuna osservazione in un campione può essere associata a un’osservazione nell’altro campione.

Questo tipo di test fa le seguenti ipotesi sui dati:

1. Indipendenza: ogni osservazione deve essere indipendente da qualsiasi altra osservazione.

2. Normalità: le differenze tra le coppie dovrebbero essere distribuite approssimativamente normalmente.

3. Nessun valore anomalo estremo: non dovrebbero esserci valori anomali estremi nelle differenze.

Se uno o più di questi presupposti non vengono soddisfatti, i risultati del t-test per campioni accoppiati potrebbero essere inaffidabili o fuorvianti.

In questo tutorial forniamo una spiegazione di ciascun presupposto, come determinare se il presupposto è soddisfatto e cosa fare se viene violato.

Ipotesi 1: Indipendenza

Un test t per campioni accoppiati presuppone che ciascuna osservazione sia indipendente da tutte le altre osservazioni.

Come verificare questa ipotesi

Il modo più semplice per verificare questa ipotesi è verificare che ciascuna osservazione sia stata raccolta utilizzando un metodo di campionamento casuale .

Se è stato utilizzato un metodo di campionamento casuale (come il campionamento casuale semplice), allora possiamo supporre che ciascuna osservazione sia indipendente da tutte le altre osservazioni.

Cosa fare se questo presupposto non viene rispettato

Se questo presupposto non è soddisfatto, i risultati del t-test per campioni accoppiati sono completamente non validi.

In questo scenario, è meglio raccogliere nuove osservazioni utilizzando un metodo di campionamento casuale per garantire che ciascuna osservazione sia indipendente.

Ipotesi 2: normalità

Un t-test per campioni accoppiati presuppone che le differenze tra le coppie debbano essere distribuite approssimativamente normalmente.

Questo è un presupposto cruciale perché se le differenze tra le coppie non sono distribuite normalmente, non è valido utilizzare il valore p del test per trarre conclusioni.

Come verificare questa ipotesi

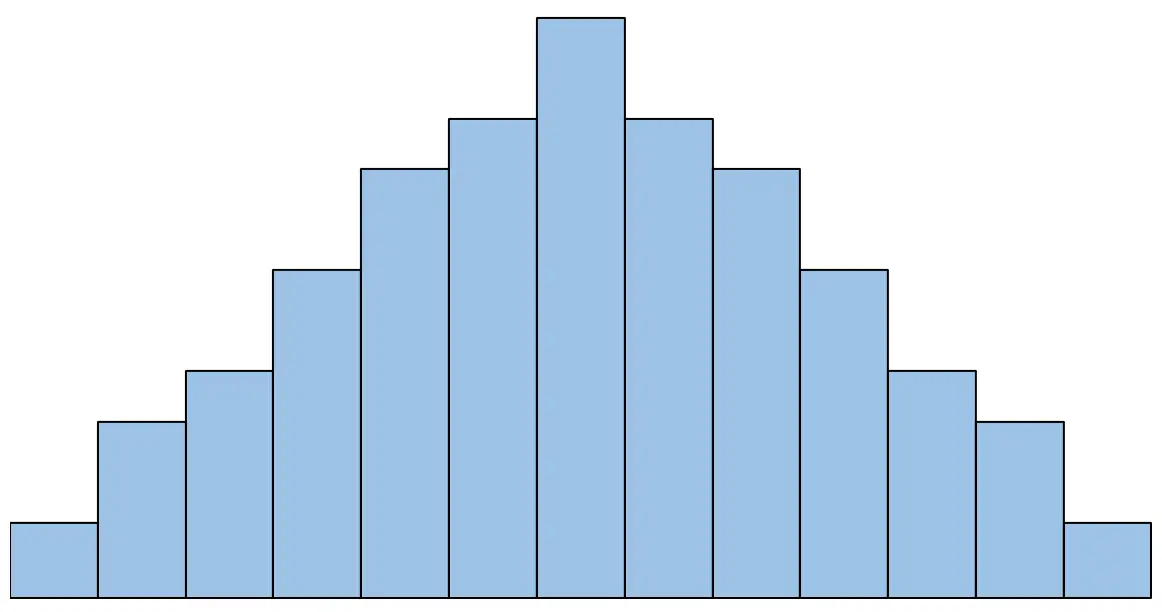
Il modo più semplice per verificare questa ipotesi è semplicemente creare un istogramma delle differenze accoppiate e verificare visivamente se l’istogramma ha o meno una forma a campana.

Ad esempio, se l’istogramma fosse simile a questo, diremmo che il presupposto di normalità è soddisfatto:

Tuttavia, se l’istogramma fosse simile a questo, diremmo che il presupposto di normalità non è soddisfatto:

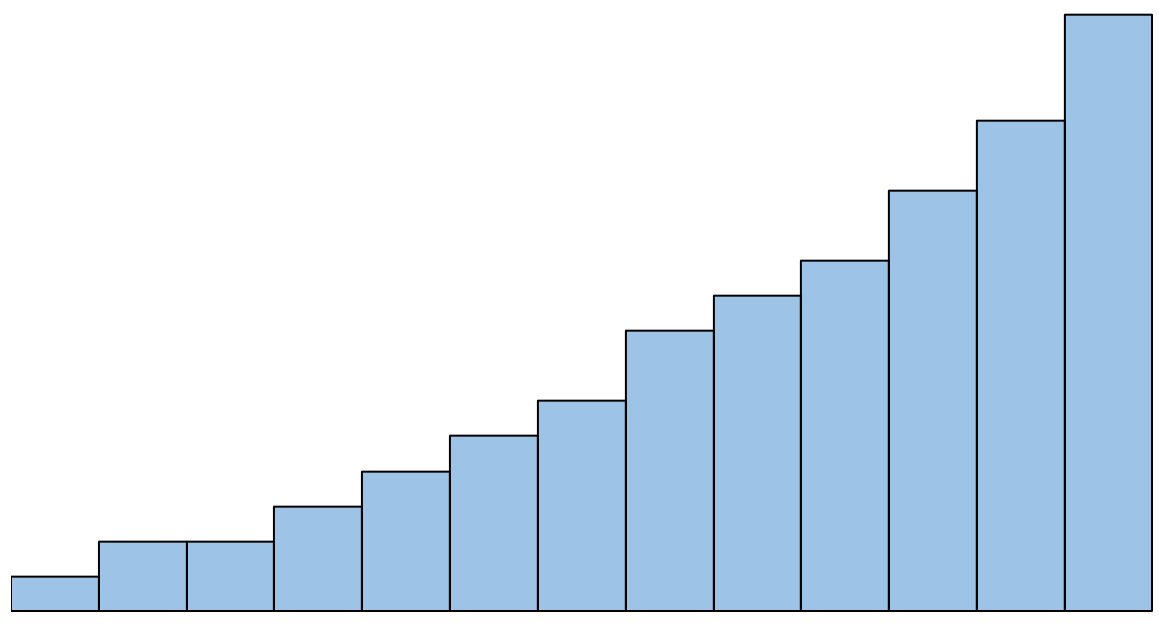
Cosa fare se questo presupposto non viene rispettato

Se questa ipotesi viene violata, possiamo eseguire un test dei ranghi con segno di Wilcoxon , che è considerato l’equivalente non parametrico del test t per campioni accoppiati e non presuppone che le differenze accoppiate siano normalmente distribuite.

Ipotesi 3: nessun valore anomalo estremo

Un t-test per campioni appaiati presuppone che non vi siano valori anomali estremi nei dati.

Come verificare questa ipotesi

Il modo più semplice per verificare questa ipotesi è creare un box plot di differenze accoppiate e verificare visivamente se sono presenti valori anomali.

Ad esempio, supponiamo che il box plot delle differenze accoppiate sia simile al seguente:

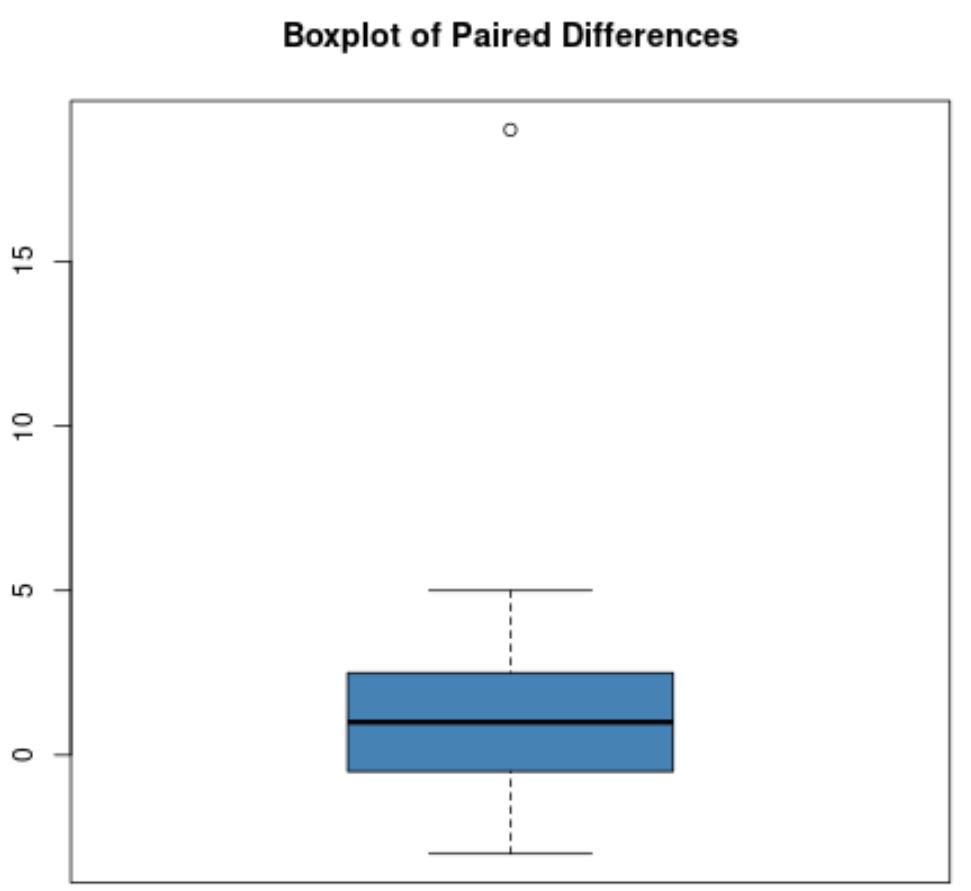
La maggior parte delle differenze tra coppie sono vicine allo zero, ma esiste una differenza pari a circa 19, che è chiaramente un valore anomalo.

Nota : in genere in un box plot viene utilizzato un cerchio per indicare un valore anomalo.

Tuttavia, supponiamo che il box plot delle differenze accoppiate sia simile al seguente:

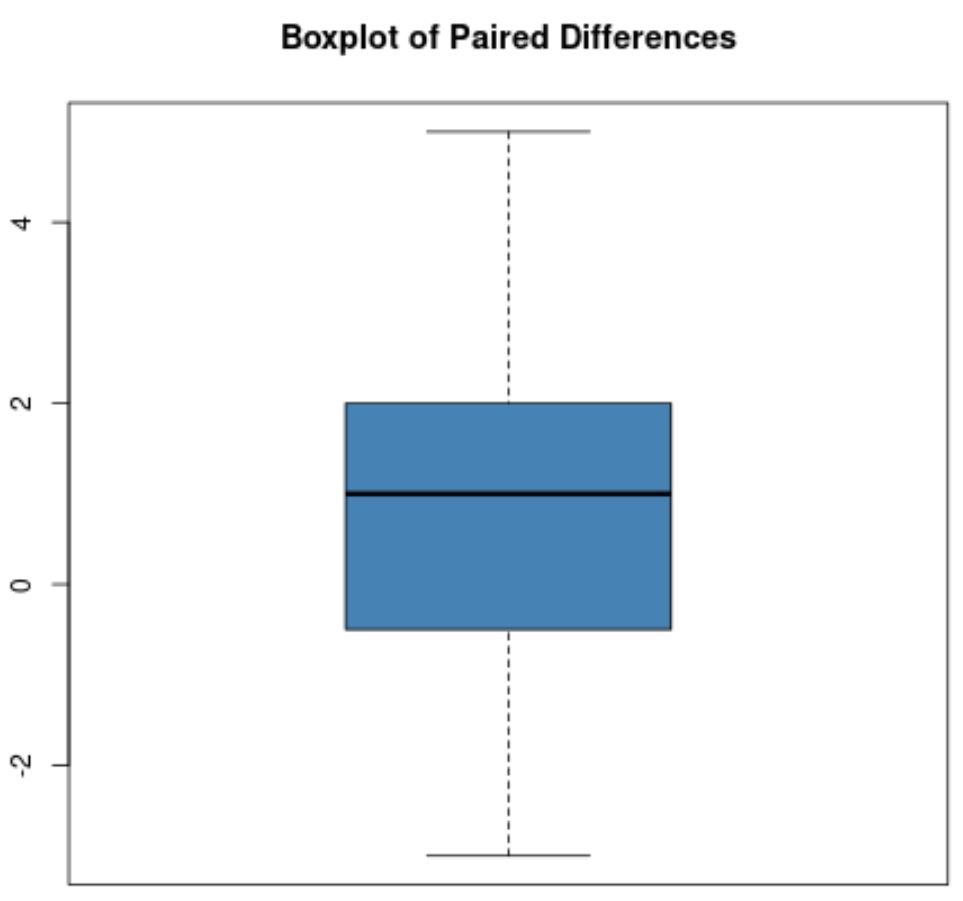
Non ci sono valori anomali chiari in questo boxplot, quindi assumeremo che non ci siano valori anomali estremi nei dati.

Cosa fare se questo presupposto non viene rispettato

Se questo presupposto viene violato, i risultati del t-test per campioni accoppiati potrebbero essere influenzati in modo anomalo dal valore anomalo.

In questo scenario, puoi rimuovere il valore anomalo se ritieni che rappresenti un punto dati errato o sia il risultato di un errore di immissione dei dati.

In alternativa, è possibile mantenere il valore anomalo e annotarlo semplicemente quando si riportano i risultati del t-test per campioni appaiati.

Risorse addizionali

I seguenti tutorial spiegano le ipotesi fatte in altri test statistici:

Le quattro ipotesi formulate in un t test
Le quattro ipotesi di un test del chi quadrato
Le quattro ipotesi dei test parametrici