Le cinque ipotesi della correlazione di pearson

Il coefficiente di correlazione di Pearson (noto anche come “coefficiente di correlazione prodotto-momento”) misura l’associazione lineare tra due variabili.

Assume sempre un valore compreso tra -1 e 1 dove:

• -1 indica una correlazione lineare perfettamente negativa tra due variabili
• 0 indica alcuna correlazione lineare tra due variabili
• 1 indica una correlazione lineare perfettamente positiva tra due variabili

Tuttavia, prima di calcolare il coefficiente di correlazione di Pearson tra due variabili, dobbiamo assicurarci che siano soddisfatte cinque ipotesi:

1. Livello di misurazione: entrambe le variabili dovrebbero essere misurate a livello di intervallo o rapporto .

2. Relazione lineare: deve esistere una relazione lineare tra le due variabili.

3. Normalità: entrambe le variabili dovrebbero avere una distribuzione approssimativamente normale.

4. Coppie correlate: ciascuna osservazione nel set di dati deve avere una coppia di valori.

5. Nessun valore anomalo: non dovrebbero esserci valori anomali estremi nel set di dati.

In questo articolo, forniamo una spiegazione di ciascun presupposto e come determinare se il presupposto è soddisfatto.

Ipotesi 1: Livello di misurazione

Per calcolare un coefficiente di correlazione di Pearson tra due variabili, entrambe le variabili devono essere misurate a livello di intervallo o rapporto .

Il grafico seguente fornisce una rapida spiegazione dei quattro livelli ai quali è possibile misurare le variabili:

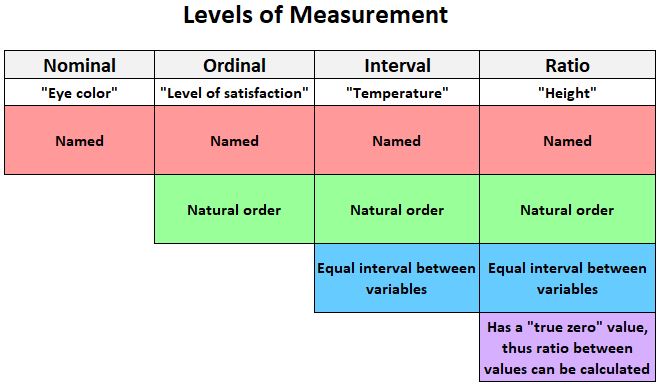
Ecco alcuni esempi di variabili che possono essere misurate su una scala a intervalli :

• Temperatura: misurata in Fahrenheit o Celsius
• Punteggi di credito: misurati da 300 a 850
• Punteggi SAT: misurati da 400 a 1.600

Ecco alcuni esempi di variabili che possono essere misurate su una scala di rapporti :

• Altezza: misurata in centimetri, pollici, piedi, ecc.
• Peso: misurato in chilogrammi, libbre, ecc.
• Lunghezza: misurata in centimetri, pollici, piedi, ecc.

Se le variabili vengono misurate a livello ordinale , è necessario calcolare il coefficiente di correlazione di Spearman tra di esse.

Correlato: Livelli di misurazione: nominale, ordinale, intervallo e rapporto

Ipotesi 2: relazione lineare

Per calcolare un coefficiente di correlazione di Pearson tra due variabili, deve esistere una relazione lineare tra le due variabili.

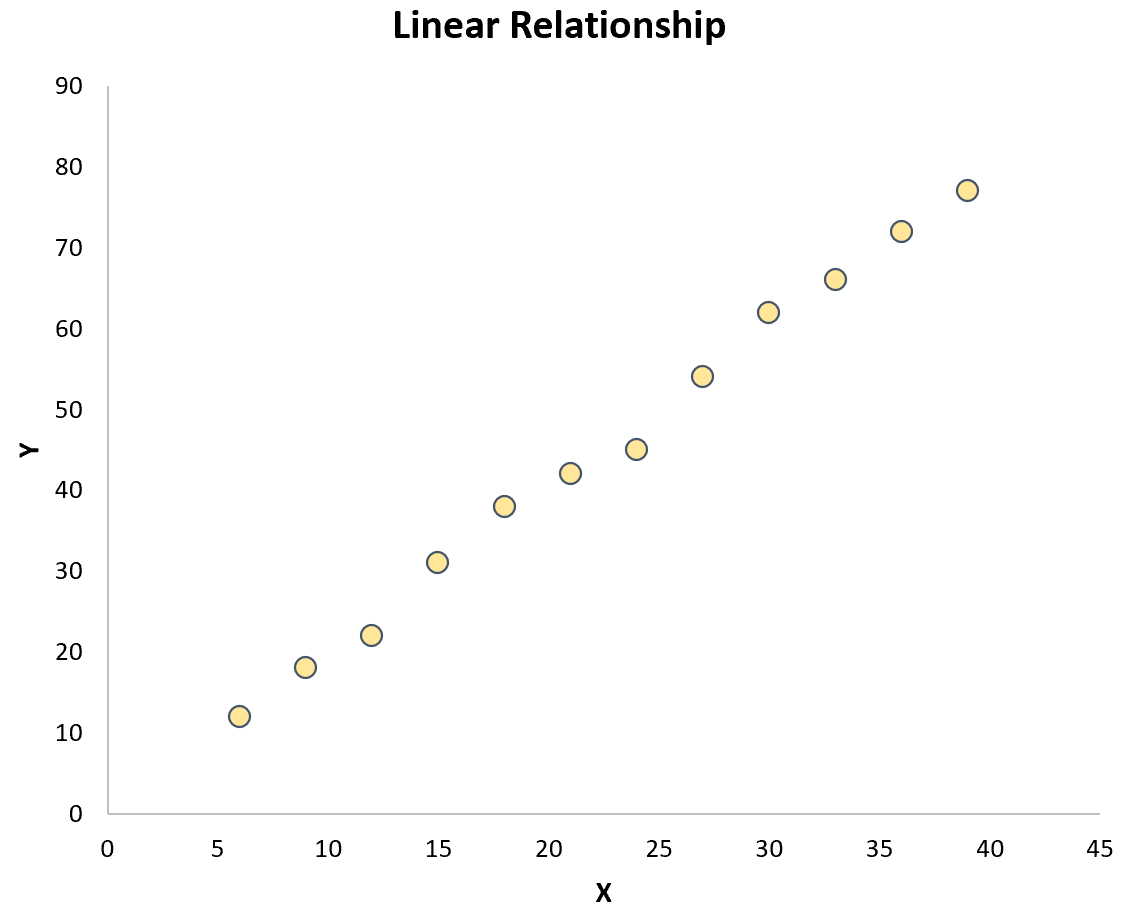
Il modo più semplice per verificare questa ipotesi è semplicemente creare un grafico a dispersione delle due variabili. Se i punti sul grafico seguono approssimativamente una linea retta, esiste una relazione lineare:

Tuttavia, se i punti sono sparsi in modo casuale nel grafico o hanno qualche altro tipo di relazione (come quella quadratica), allora non esiste una relazione lineare tra le variabili:

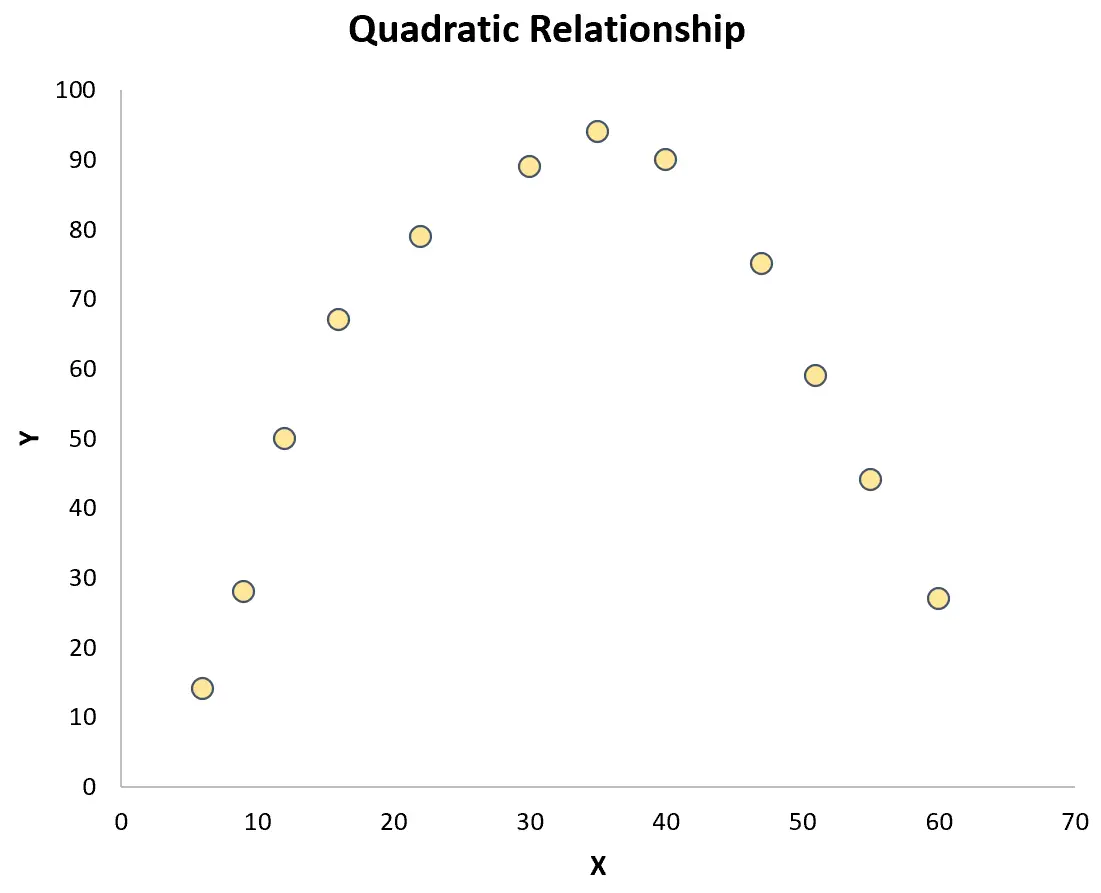
In questo caso, un coefficiente di correlazione di Pearson non catturerà adeguatamente la relazione tra le variabili.

Ipotesi 3: normalità

Un coefficiente di correlazione di Pearson presuppone inoltre che le due variabili siano distribuite approssimativamente normalmente .

È possibile verificare visivamente questo presupposto creando un istogramma o un grafico QQ per ciascuna variabile.

1. Istogramma

Se l’istogramma di un set di dati ha approssimativamente la forma di una campana, è probabile che i dati siano distribuiti normalmente.

2. QQLand

Un grafico QQ, abbreviazione di “quantile-quantile”, è un tipo di grafico che mostra i quantili teorici lungo l’asse x (ovvero dove si troverebbero i dati se seguissero una distribuzione normale) e i quantili dei campioni lungo l’asse y. (cioè dove risiedono effettivamente i tuoi dati).

Se i valori dei dati seguono una linea approssimativamente retta che forma un angolo di 45 gradi, si presuppone che i dati siano distribuiti normalmente.

È inoltre possibile eseguire un test statistico formale per determinare se una variabile è distribuita normalmente.

Se il valore p del test è inferiore a un certo livello di significatività (come α = 0,05), allora hai prove sufficienti per affermare che i dati non sono distribuiti normalmente.

Esistono tre test statistici comunemente utilizzati per testare la normalità:

1. Il test di Jarque-Bera

• Come eseguire un test Jarque-Bera in Excel
• Come eseguire un test Jarque-Bera in R
• Come eseguire un test Jarque-Bera in Python

2. Il test di Shapiro-Wilk

• Come eseguire un test di Shapiro-Wilk in R
• Come eseguire un test di Shapiro-Wilk in Python

3. Il test di Kolmogorov-Smirnov

• Come eseguire un test di Kolmogorov-Smirnov in R
• Come eseguire un test di Kolmogorov-Smirnov in Python

Ipotesi 4: coppie correlate

Un coefficiente di correlazione di Pearson presuppone inoltre che ciascuna osservazione nel set di dati debba avere una coppia di valori.

Questa ipotesi è facile da verificare. Ad esempio, se stai calcolando la correlazione tra peso e altezza, verifica semplicemente che ciascuna osservazione nel set di dati abbia una misura per il peso e una misura per l’altezza.

Ipotesi 5: Nessun valore anomalo

Un coefficiente di correlazione di Pearson presuppone inoltre che non vi siano valori anomali estremi nel set di dati, poiché i valori anomali influenzano fortemente il calcolo del coefficiente di correlazione.

Per illustrare ciò, si consideri il seguente set di dati:

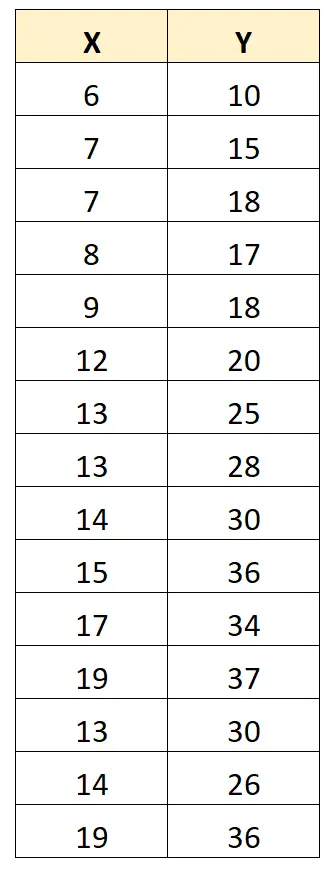
Il coefficiente di correlazione di Pearson tra X e Y è 0,949 .

Tuttavia, supponiamo di avere un valore anomalo nel set di dati:

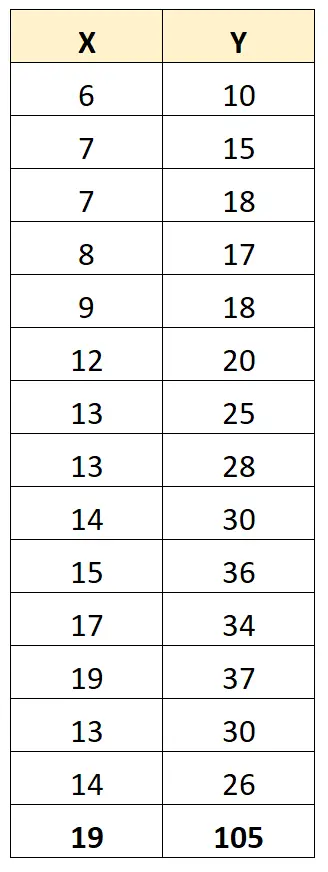
Il coefficiente di correlazione di Pearson tra X e Y è ora 0,711 .

Un valore anomalo modifica significativamente il coefficiente di correlazione di Pearson tra le due variabili. In questo caso, potrebbe avere senso rimuovere il valore anomalo dal set di dati.

Correlato: La guida completa: quando rimuovere i valori anomali nei dati

Risorse addizionali

Le seguenti esercitazioni forniscono ulteriori informazioni sulla correlazione di Pearson:

Introduzione al coefficiente di correlazione di Pearson
Come riportare la correlazione di Pearson in formato APA
Come calcolare manualmente un coefficiente di correlazione di Pearson