Come verificare le ipotesi anova

Un’ANOVA unidirezionale è un test statistico utilizzato per determinare se esiste o meno una differenza significativa tra le medie di tre o più gruppi indipendenti.

Ecco un esempio di quando potremmo utilizzare un’ANOVA unidirezionale:

Dividi casualmente una classe di 90 studenti in tre gruppi di 30. Ciascun gruppo utilizza una tecnica di studio diversa per un mese per prepararsi a un esame. Alla fine del mese tutti gli studenti sostengono lo stesso esame.

Vuoi sapere se la tecnica di studio ha o meno un impatto sui punteggi degli esami. Quindi esegui un’ANOVA unidirezionale per determinare se esiste una differenza statisticamente significativa tra i punteggi medi dei tre gruppi.

Prima di poter eseguire un’ANOVA unidirezionale, dobbiamo prima verificare che siano soddisfatte tre ipotesi.

1. Normalità – Ogni campione è stato estratto da una popolazione distribuita normalmente.

2. Varianze uguali – Le varianze delle popolazioni da cui vengono estratti i campioni sono uguali.

3. Indipendenza – Le osservazioni all’interno di ciascun gruppo sono indipendenti l’una dall’altra e le osservazioni all’interno dei gruppi sono state ottenute mediante campionamento casuale.

Se queste ipotesi non vengono soddisfatte, i risultati della nostra ANOVA unidirezionale potrebbero non essere affidabili.

In questo articolo spieghiamo come verificare questi presupposti e cosa fare se qualcuno di essi viene violato.

Presupposto n. 1: normalità

L’ANOVA presuppone che ciascun campione sia stato estratto da una popolazione distribuita normalmente.

Come verificare questa ipotesi in R:

Per verificare questa ipotesi possiamo utilizzare due approcci:

• Verificare visivamente l’ipotesi utilizzando istogrammi o grafici QQ .
• Verifica l’ipotesi utilizzando test statistici formali come Shapiro-Wilk, Kolmogorov-Smironov, Jarque-Barre o D’Agostino-Pearson.

Ad esempio, supponiamo di reclutare 90 persone per partecipare a un esperimento sulla perdita di peso in cui assegniamo casualmente 30 persone a seguire il Programma A, il Programma B o il Programma C per un mese. Per vedere se il programma ha un impatto sulla perdita di peso, vogliamo eseguire un’ANOVA unidirezionale. Il codice seguente illustra come verificare il presupposto di normalità utilizzando istogrammi, grafici QQ e un test di Shapiro-Wilk.

1. Montare il modello ANOVA.

 #make this example reproducible
set.seed(0)

#create data frame
data <- data. frame (program = rep(c(" A ", " B ", " C "), each = 30 ),
                   weight_loss = c(runif(30, 0, 3),
                                   runif(30, 0, 5),
                                   runif(30, 1, 7)))

#fit the one-way ANOVA model
model <- aov(weight_loss ~ program, data = data)

2. Creare un istogramma dei valori di risposta.

 #create histogram
hist(data$weight_loss)

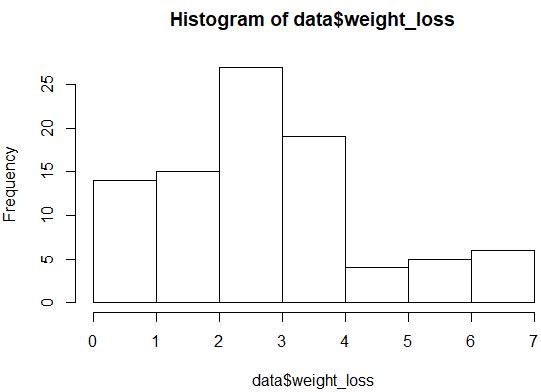
La distribuzione non sembra distribuita in modo molto normale (ad esempio non è a forma di “campana”), ma possiamo anche creare un grafico QQ per dare un’altra occhiata alla distribuzione.

3. Creare un grafico QQ dei residui

 #create QQ plot to compare this dataset to a theoretical normal distribution
qqnorm(model$residuals)

#add straight diagonal line to plot
qqline(model$residuals) 

In generale, se i punti dati si trovano lungo una linea diagonale retta in un grafico QQ, è probabile che il set di dati segua una distribuzione normale. In questo caso possiamo vedere che c’è una notevole deviazione dalla linea lungo le estremità, il che potrebbe indicare che i dati non sono distribuiti normalmente.

4. Eseguire il test di Shapiro-Wilk per verificare la normalità.

 #Conduct Shapiro-Wilk Test for normality
shapiro. test (data$weight_loss)

#Shapiro-Wilk normality test
#
#data: data$weight_loss
#W = 0.9587, p-value = 0.005999

Il test di Shapiro-Wilk verifica l’ipotesi nulla che i campioni provengano da una distribuzione normale rispetto all’ipotesi alternativa che i campioni non provengano da una distribuzione normale. In questo caso, il valore p del test è 0,005999 , che è inferiore al livello alfa di 0,05. Ciò suggerisce che i campioni non seguono una distribuzione normale.

Cosa fare se questo presupposto non viene rispettato:

In generale, un’ANOVA unidirezionale è considerata abbastanza robusta contro le violazioni del presupposto di normalità purché le dimensioni del campione siano sufficientemente grandi.

Inoltre, se disponi di campioni estremamente grandi, test statistici come il test di Shapiro-Wilk ti diranno quasi sempre che i tuoi dati non sono normali. Per questo motivo, spesso è meglio ispezionare visivamente i dati utilizzando grafici come istogrammi e grafici QQ. Basta osservare i grafici per capire se i dati sono distribuiti normalmente oppure no.

Se il presupposto della normalità è gravemente violato o vuoi semplicemente essere molto conservatore, hai due scelte:

(1) Trasforma i valori di risposta dei tuoi dati in modo che le distribuzioni siano distribuite più normalmente.

(2) Eseguire un test non parametrico equivalente come un test di Kruskal-Wallis che non richiede l’assunzione di normalità.

Presupposto n. 2: varianza uguale

L’ANOVA presuppone che le varianze delle popolazioni da cui vengono estratti i campioni siano uguali.

Come verificare questa ipotesi in R:

Possiamo verificare questa ipotesi in R utilizzando due approcci:

• Verificare visivamente l’ipotesi utilizzando boxplot.
• Verifica l’ipotesi utilizzando test statistici formali come il test di Bartlett.

Il codice seguente mostra come eseguire questa operazione, utilizzando lo stesso set di dati sulla perdita di peso falso creato in precedenza.

1. Crea box plot.

 #Create box plots that show distribution of weight loss for each group
boxplot(weight_loss ~ program, xlab=' Program ', ylab=' Weight Loss ', data=data)

La varianza nella perdita di peso in ciascun gruppo può essere osservata dalla lunghezza di ciascun boxplot. Più lunga è la scatola, maggiore è la varianza. Ad esempio, possiamo vedere che la varianza è leggermente superiore per i partecipanti al Programma C rispetto al Programma A e al Programma B.

2. Eseguire il test Bartlett.

 #Create box plots that show distribution of weight loss for each group
bartlett. test (weight_loss ~ program, data=data)

#Bartlett test of homogeneity of variances
#
#data: weight_loss by program
#Bartlett's K-squared = 8.2713, df = 2, p-value = 0.01599

Il test di Bartlett verifica l’ipotesi nulla che i campioni abbiano varianze uguali rispetto all’ipotesi alternativa che i campioni non abbiano varianze uguali. In questo caso, il valore p del test è 0,01599 , che è inferiore al livello alfa di 0,05. Ciò suggerisce che i campioni non presentano tutti la stessa varianza.

Cosa fare se questo presupposto non viene rispettato:

In generale, un’ANOVA unidirezionale è considerata abbastanza robusta rispetto alle violazioni del presupposto di uguaglianza delle varianze purché ciascun gruppo abbia la stessa dimensione campionaria.

Tuttavia, se le dimensioni del campione non sono le stesse e questo presupposto viene gravemente violato, è possibile eseguire invece un test Kruskal-Wallis , che è la versione non parametrica dell’ANOVA unidirezionale.

Presupposto n. 3: indipendenza

L’ANOVA presuppone:

• Le osservazioni di ciascun gruppo sono indipendenti dalle osservazioni di tutti gli altri gruppi.
• Le osservazioni all’interno di ciascun gruppo sono state ottenute da un campione casuale.

Come verificare questa ipotesi:

Non esiste un test formale da utilizzare per verificare che le osservazioni in ciascun gruppo siano indipendenti e che siano state ottenute da un campione casuale. L’unico modo per soddisfare questo presupposto è utilizzare un disegno randomizzato.

Cosa fare se questo presupposto non viene rispettato:

Sfortunatamente, non c’è molto che puoi fare se questo presupposto non viene soddisfatto. In parole povere, se i dati fossero raccolti in modo tale che le osservazioni in ciascun gruppo non fossero indipendenti dalle osservazioni in altri gruppi, o se le osservazioni all’interno di ciascun gruppo non fossero ottenute mediante un processo randomizzato, i risultati ANOVA non sarebbero affidabili .

Se questo presupposto non è soddisfatto, la cosa migliore da fare è ricreare l’esperimento utilizzando un disegno randomizzato.

Ulteriori letture:

Come eseguire l’ANOVA unidirezionale in R
Come eseguire ANOVA unidirezionale in Excel