Le quattro ipotesi della regressione lineare

La regressione lineare è un metodo statistico utile che possiamo utilizzare per comprendere la relazione tra due variabili, x e y. Tuttavia, prima di eseguire una regressione lineare, dobbiamo prima assicurarci che siano soddisfatte quattro ipotesi:

1. Relazione lineare: esiste una relazione lineare tra la variabile indipendente, x, e la variabile dipendente, y.

2. Indipendenza: i residui sono indipendenti. In particolare, non esiste alcuna correlazione tra i residui consecutivi nei dati delle serie temporali.

3. Omoschedasticità: i residui hanno una varianza costante ad ogni livello di x.

4. Normalità: i residui del modello sono distribuiti normalmente.

Se uno o più di questi presupposti non vengono soddisfatti, i risultati della nostra regressione lineare potrebbero essere inaffidabili o addirittura fuorvianti.

In questo articolo forniamo una spiegazione per ciascun presupposto, come determinare se il presupposto è soddisfatto e cosa fare se il presupposto non è soddisfatto.

Ipotesi 1: relazione lineare

Spiegazione

Il primo presupposto della regressione lineare è che esista una relazione lineare tra la variabile indipendente x e la variabile indipendente y.

Come determinare se questo presupposto è soddisfatto

Il modo più semplice per verificare se questo presupposto è soddisfatto è creare un grafico a dispersione di x rispetto a y. Ciò consente di vedere visivamente se esiste una relazione lineare tra le due variabili. Se sembra che i punti sul grafico possano giacere lungo una linea retta, allora esiste un qualche tipo di relazione lineare tra le due variabili e questo presupposto è soddisfatto.

Ad esempio, i punti nel grafico seguente sembrano cadere su una linea retta, indicando che esiste una relazione lineare tra x e y:

Tuttavia, non sembra esserci una relazione lineare tra x e y nel grafico seguente:

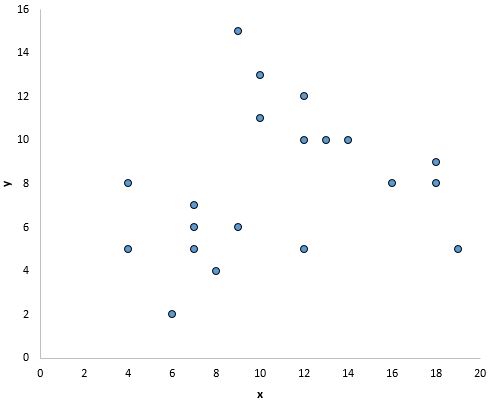
E in questo grafico sembra esserci una chiara relazione tra x e y, ma non una relazione lineare :

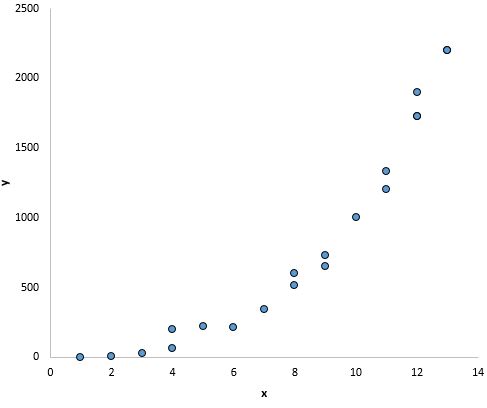
Cosa fare se questo presupposto non viene rispettato

Se crei un grafico a dispersione di valori per xey e scopri che non esiste una relazione lineare tra le due variabili, hai diverse opzioni:

1. Applicare una trasformazione non lineare alla variabile indipendente e/o dipendente. Esempi comuni includono il logaritmo, la radice quadrata o il reciproco della variabile indipendente e/o dipendente.

2. Aggiungi un’altra variabile indipendente al modello. Ad esempio, se il grafico di x rispetto a y ha una forma parabolica, potrebbe avere senso aggiungere X ² come variabile indipendente aggiuntiva nel modello.

Ipotesi 2: Indipendenza

Spiegazione

Il successivo presupposto della regressione lineare è che i residui siano indipendenti. Ciò è particolarmente rilevante quando si lavora con dati di serie temporali. Idealmente, non vogliamo che ci sia una tendenza tra residui consecutivi. Ad esempio, i residui non dovrebbero aumentare continuamente nel tempo.

Come determinare se questo presupposto è soddisfatto

Il modo più semplice per verificare se questa ipotesi è valida è osservare un grafico dei residui della serie temporale, che è un grafico dei residui rispetto al tempo. Idealmente, la maggior parte delle autocorrelazioni residue dovrebbe rientrare nelle bande di confidenza del 95% attorno allo zero, che si trovano a circa +/- 2 sulla radice quadrata di n , dove n è la dimensione del campione. Puoi anche verificare formalmente se questo presupposto è soddisfatto utilizzando il test di Durbin-Watson .

Cosa fare se questo presupposto non viene rispettato

A seconda di come viene violato questo presupposto, hai diverse opzioni:

• Per una correlazione seriale positiva, prendere in considerazione l’aggiunta di ritardi della variabile dipendente e/o indipendente al modello.
• Per la correlazione seriale negativa, assicurati che nessuna delle variabili abbia un ritardo eccessivo .
• Per la correlazione stagionale, prendere in considerazione l’aggiunta di dummy stagionali al modello.

Ipotesi 3: Omoschedasticità

Spiegazione

Il successivo presupposto della regressione lineare è che i residui abbiano varianza costante a ciascun livello di x. Questa si chiama omoschedasticità . Quando questo non è il caso, i residui soffrono di eteroschedasticità .

Quando l’eteroschedasticità è presente in un’analisi di regressione, i risultati dell’analisi diventano difficili da credere. Nello specifico, l’eteroschedasticità aumenta la varianza delle stime dei coefficienti di regressione, ma il modello di regressione non ne tiene conto. Ciò rende molto più probabile che un modello di regressione affermi che un termine nel modello è statisticamente significativo, quando in realtà non lo è.

Come determinare se questo presupposto è soddisfatto

Il modo più semplice per rilevare l’eteroschedasticità è creare un grafico valore/residuo adattato .

Una volta adattata una linea di regressione a un set di dati, è possibile creare un grafico a dispersione che mostra i valori adattati del modello rispetto ai residui di tali valori adattati. Il grafico a dispersione seguente mostra un grafico tipico del valore adattato rispetto al residuo in cui è presente l’eteroschedasticità.

Notare come i residui si diffondono sempre di più all’aumentare dei valori adattati. Questa forma a “cono” è un classico segno di eteroschedasticità:

Cosa fare se questo presupposto non viene rispettato

Esistono tre modi comuni per correggere l’eteroschedasticità:

1. Trasforma la variabile dipendente. Una trasformazione comune consiste semplicemente nel prendere il logaritmo della variabile dipendente. Ad esempio, se utilizziamo la dimensione della popolazione (variabile indipendente) per prevedere il numero di fioristi in una città (variabile dipendente), possiamo invece provare a utilizzare la dimensione della popolazione per prevedere il logaritmo del numero di fioristi in una città. L’utilizzo del logaritmo della variabile dipendente, anziché della variabile dipendente originale, spesso comporta la scomparsa dell’eteroschedasticità.

2. Ridefinire la variabile dipendente. Un modo comune per ridefinire la variabile dipendente è utilizzare un tasso anziché il valore grezzo. Ad esempio, invece di utilizzare la dimensione della popolazione per prevedere il numero di fioristi in una città, possiamo utilizzare la dimensione della popolazione per prevedere il numero di fioristi pro capite. Nella maggior parte dei casi, ciò riduce la variabilità che si verifica naturalmente all’interno di popolazioni più grandi poiché misuriamo il numero di fioristi per persona, piuttosto che il numero di fioristi stessi.

3. Utilizzare la regressione ponderata. Un altro modo per correggere l’eteroschedasticità è utilizzare la regressione ponderata. Questo tipo di regressione assegna un peso a ciascun punto dati in base alla varianza del relativo valore adattato. In sostanza, ciò attribuisce pesi bassi ai punti dati che presentano varianze più elevate, riducendo i loro quadrati residui. Quando vengono utilizzati i pesi appropriati, ciò può eliminare il problema dell’eteroschedasticità.

Ipotesi 4: normalità

Spiegazione

Il successivo presupposto della regressione lineare è che i residui siano distribuiti normalmente.

Come determinare se questo presupposto è soddisfatto

Esistono due modi comuni per verificare se questa ipotesi è soddisfatta:

1. Verificare visivamente l’ipotesi utilizzando i grafici QQ .

Un grafico QQ, abbreviazione di grafico quantile-quantile, è un tipo di grafico che possiamo utilizzare per determinare se i residui di un modello seguono o meno una distribuzione normale. Se i punti sul grafico formano approssimativamente una linea diagonale retta, il presupposto di normalità è soddisfatto.

Il seguente grafico QQ mostra un esempio di residui che seguono approssimativamente una distribuzione normale:

Tuttavia, il grafico QQ riportato di seguito mostra un esempio di un caso in cui i residui deviano chiaramente da una linea diagonale retta, indicando che non seguono la distribuzione normale:

2. Puoi anche verificare l’ipotesi di normalità utilizzando test statistici formali come Shapiro-Wilk, Kolmogorov-Smironov, Jarque-Barre o D’Agostino-Pearson. Tuttavia, tieni presente che questi test sono sensibili alle dimensioni del campione di grandi dimensioni, ovvero spesso concludono che i residui non sono normali quando la dimensione del campione è ampia. Questo è il motivo per cui spesso è più semplice utilizzare semplicemente metodi grafici come un grafico QQ per verificare questa ipotesi.

Cosa fare se questo presupposto non viene rispettato

Se il presupposto di normalità non viene soddisfatto, hai diverse opzioni:

• Innanzitutto, controlla che i valori anomali non abbiano un impatto enorme sulla distribuzione. Se sono presenti valori anomali, assicurarsi che siano valori reali e non errori di immissione dei dati.
• Quindi è possibile applicare una trasformazione non lineare alla variabile indipendente e/o dipendente. Esempi comuni includono il logaritmo, la radice quadrata o il reciproco della variabile indipendente e/o dipendente.

Ulteriori letture:

Introduzione alla regressione lineare semplice
Comprendere l’eteroschedasticità nell’analisi di regressione
Come creare e interpretare un grafico QQ in R