L'ipotesi della varianza costante: definizione ed esempio

La regressione lineare è una tecnica che utilizziamo per quantificare la relazione tra una o più variabili predittive e una variabile di risposta .

Uno dei presupposti chiave della regressione lineare è che i residui abbiano una varianza costante a ciascun livello delle variabili predittive.

Se questa assunzione non fosse verificata, i residui soffrirebbero di eteroschedasticità . Quando ciò accade, le stime dei coefficienti del modello diventano inaffidabili.

Come valutare la varianza costante

Il modo più comune per determinare se i residui di un modello di regressione hanno una varianza costante è creare un grafico dei valori adattati rispetto ai residui .

Questo è un tipo di grafico che mostra i valori adattati del modello di regressione lungo l’asse x e i residui di tali valori adattati lungo l’asse y.

Se la distribuzione dei residui è approssimativamente uguale a ciascun livello dei valori adattati, diciamo che l’ipotesi di varianza costante è soddisfatta.

Altrimenti, se la dispersione dei residui aumenta o diminuisce sistematicamente, questa assunzione è probabilmente violata.

Nota : questo tipo di grafico può essere creato solo dopo aver adattato un modello di regressione al set di dati.

Il grafico seguente mostra un esempio di un grafico di valori adattati rispetto ai residui che mostra una varianza costante :

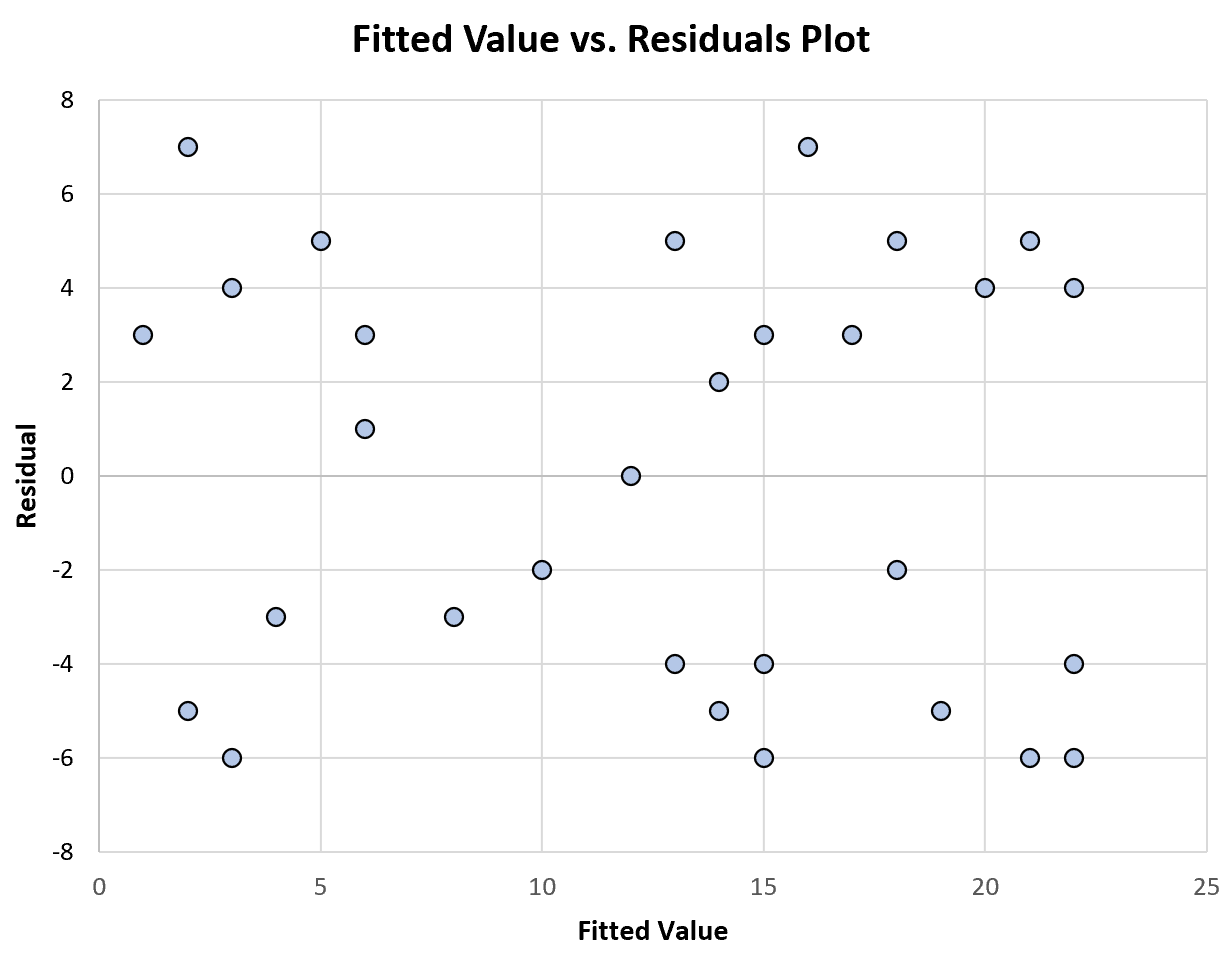
Si noti come i residui siano sparsi in modo casuale attorno allo zero, senza uno schema particolare, con una varianza approssimativamente costante a ciascun livello dei valori adattati.

Il grafico seguente mostra un esempio di un grafico di valori adattati rispetto ai residui che mostra una varianza non costante :

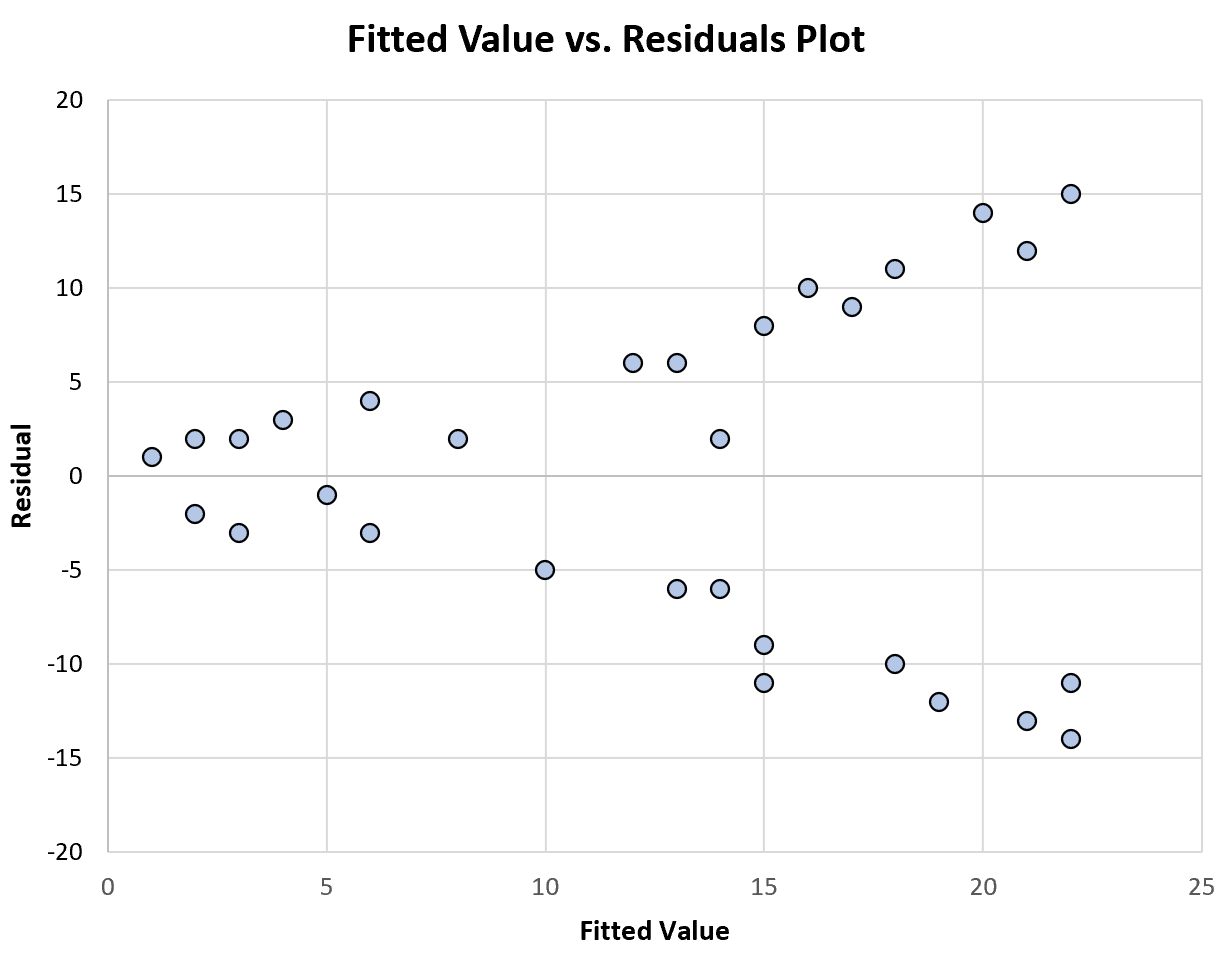
Si noti che la distribuzione dei residui diventa maggiore all’aumentare dei valori adattati. Questo è un tipico segno di varianza non costante.

Questo ci dice che il nostro modello di regressione soffre di una varianza non costante nei residui e che le stime dei coefficienti del modello sono quindi inaffidabili.

Come correggere una violazione della varianza costante

Se il presupposto della varianza costante viene violato, il modo più comune per risolvere questo problema è trasformare la variabile di risposta utilizzando una delle tre trasformazioni:

1. Trasformazione del log: trasforma la variabile di risposta da y a log(y)

2. Trasformazione della radice quadrata: trasforma la variabile di risposta da y a √y

3. Trasformazione della radice del cubo: trasforma la variabile di risposta da y a y ^1/3

Eseguendo queste trasformazioni il problema della varianza non costante generalmente scompare.

Risorse addizionali

Le seguenti esercitazioni forniscono informazioni aggiuntive sulla regressione lineare e sull’analisi dei residui:

Introduzione alla regressione lineare semplice
Introduzione alla regressione lineare multipla
Le quattro ipotesi della regressione lineare
Cosa sono i residui in statistica?