La guida completa: come verificare le ipotesi manova

Una MANOVA (analisi multivariata della varianza) viene utilizzata per analizzare come una o più variabili fattore influenzano le variabili a risposta multipla.

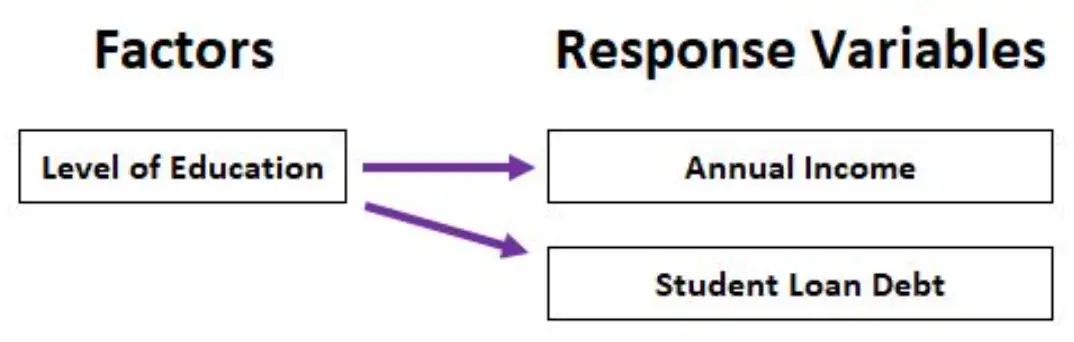
Ad esempio, potremmo utilizzare una MANOVA per analizzare in che modo il livello di istruzione (diploma di scuola superiore, laurea, laurea triennale, laurea magistrale) influisce sia sul reddito annuale che sul debito totale del prestito studentesco.

Correlati: Le differenze tra ANOVA, ANCOVA, MANOVA e MANCOVA

Ogni volta che eseguiamo una MANOVA, dobbiamo verificare che siano soddisfatte le seguenti ipotesi:

1. Normalità multivariata – Le variabili di risposta sono multivariate normalmente distribuite all’interno di ciascun gruppo di variabili fattore.

2. Indipendenza – Ogni osservazione viene campionata in modo casuale e indipendente dalla popolazione.

3. Varianza uguale – Le matrici di covarianza della popolazione di ciascun gruppo sono uguali.

4. Nessun valore anomalo multivariato : non sono presenti valori anomali multivariati estremi.

In questo articolo, forniamo una spiegazione di ciascun presupposto e come determinare se il presupposto è soddisfatto.

Presupposto 1: normalità multivariata

Una MANOVA presuppone che le variabili di risposta siano multivariate normalmente distribuite all’interno di ciascun gruppo della variabile fattore.

Se ci sono almeno 20 osservazioni per ciascuna combinazione fattore * variabile di risposta, allora possiamo supporre che l’ipotesi di normalità multivariata sia soddisfatta.

Se ci sono meno di 20 osservazioni per ciascuna combinazione fattore*variabile di risposta, possiamo creare una matrice di grafico a dispersione per visualizzare i residui e verificare visivamente se questo presupposto è soddisfatto.

Fortunatamente, è noto che MANOVA è resistente alle deviazioni dalla normalità multivariata, quindi deviazioni da piccole a moderate generalmente non sono un problema.

Ipotesi 2: Indipendenza

Una MANOVA presuppone che ogni osservazione sia campionata in modo casuale e indipendente dalla popolazione.

Finché per raccogliere i dati viene utilizzato un metodo di campionamento probabilistico (ogni membro di una popolazione ha la stessa probabilità di essere selezionato per far parte del campione), possiamo supporre che ciascuna osservazione sia stata campionata in modo casuale e indipendente.

Esempi di metodi di campionamento probabilistico includono:

• Campionamento casuale semplice
• Campionamento casuale stratificato
• Campionamento casuale di cluster
• Campionamento casuale sistematico

Ipotesi 3: varianza uguale

Una MANOVA presuppone che le matrici di covarianza della popolazione di ciascun gruppo siano uguali.

Il modo più comune per verificare questa ipotesi è utilizzare il test M di Box. Questo test è noto per essere piuttosto rigoroso, motivo per cui generalmente utilizziamo un livello di significatività pari a 0,001 per determinare se le matrici di covarianza della popolazione sono uguali o meno.

Se il valore p del test M di Box è maggiore di 0,001, possiamo supporre che questa ipotesi sia soddisfatta.

Fortunatamente, anche se il valore p del test è inferiore a 0,001, una MANOVA tende ad essere robusta rispetto alle deviazioni da questa ipotesi.

Affinché le matrici di covarianza non uguali costituiscano un problema, le differenze tra le matrici di covarianza devono essere piuttosto estreme.

Ipotesi 4: nessun valore anomalo multivariato

Una MANOVA presuppone che nei dati non siano presenti valori anomali multivariati estremi che potrebbero influenzare in modo significativo i risultati.

Il modo più comune per verificare questa ipotesi è calcolare la distanza di Mahalanobis per ciascuna osservazione, che rappresenta la distanza tra due punti in uno spazio multivariato.

Se il valore p corrispondente per una distanza Mahalanobis di un’osservazione è inferiore a 0,001, generalmente dichiariamo che l’osservazione è un valore anomalo estremo.

Fare riferimento ai seguenti tutorial per vedere come calcolare la distanza Mahalanobis in vari software statistici:

• Come calcolare la distanza di Mahalanobis in R
• Come calcolare la distanza di Mahalanobis in SPSS
• Come calcolare la distanza di Mahalanobis in Python

Risorse addizionali

I seguenti tutorial spiegano come eseguire una MANOVA in vari software statistici:

Come eseguire una MANOVA in R
Come eseguire una MANOVA in SPSS
Come eseguire una MANOVA in Stata