Comprensione dell'ipotesi nulla per i modelli anova

Un’ANOVA unidirezionale viene utilizzata per determinare se esiste una differenza statisticamente significativa tra le medie di tre o più gruppi indipendenti.

Un’ANOVA unidirezionale utilizza le seguenti ipotesi nulle e alternative:

• H ₀ : μ ₁ = μ ₂ = μ ₃ = … = μ _k (tutte le medie dei gruppi sono uguali)
• H _A : Almeno una media del gruppo è diversa   riposo

Per decidere se rifiutare o meno l’ipotesi nulla, dobbiamo fare riferimento al valore p nel risultato della tabella ANOVA.

Se il valore p è inferiore a un certo livello di significatività (ad esempio 0,05), allora possiamo rifiutare l’ipotesi nulla e concludere che non tutte le medie dei gruppi sono uguali.

Un’ANOVA a due vie viene utilizzata per determinare se esiste o meno una differenza statisticamente significativa tra le medie di tre o più gruppi indipendenti assegnati a due variabili (a volte chiamate “fattori”).

Un’ANOVA a due vie verifica tre ipotesi nulle contemporaneamente:

• Tutte le medie dei gruppi sono uguali a ciascun livello della prima variabile
• Tutte le medie dei gruppi sono uguali a ciascun livello della seconda variabile
• Non vi è alcun effetto di interazione tra le due variabili

Per decidere se rifiutare o meno ogni ipotesi nulla, dobbiamo fare riferimento ai valori p nel risultato della tabella ANOVA a due vie.

Gli esempi seguenti mostrano come decidere se rifiutare o meno l’ipotesi nulla in un’ANOVA a una via e in un’ANOVA a due vie.

Esempio 1: ANOVA unidirezionale

Supponiamo di voler sapere se tre diversi programmi di preparazione al test portano o meno a punteggi medi diversi in un dato esame. Per testarlo, reclutiamo 30 studenti per partecipare a uno studio e li dividiamo in tre gruppi.

Gli studenti di ciascun gruppo vengono assegnati in modo casuale a utilizzare uno dei tre programmi di preparazione al test per le tre settimane successive per prepararsi a un esame. Alla fine delle tre settimane, tutti gli studenti sostengono lo stesso esame.

Di seguito sono riportati i risultati degli esami per ciascun gruppo:

Quando inseriamo questi valori nel calcolatore ANOVA unidirezionale , riceviamo come output la seguente tabella ANOVA:

Si noti che il valore p è 0,11385 .

Per questo esempio particolare, utilizzeremmo le seguenti ipotesi nulle e alternative:

• H ₀ : μ ₁ = μ ₂ = μ ₃ (il punteggio medio dell’esame per ciascun gruppo è uguale)
• H _A : Almeno una media del gruppo è diversa   riposo

Poiché il valore p della tabella ANOVA non è inferiore a 0,05, non riusciamo a rifiutare l’ipotesi nulla.

Ciò significa che non abbiamo prove sufficienti per affermare che esiste una differenza statisticamente significativa tra i punteggi medi degli esami dei tre gruppi.

Esempio 2: ANOVA bidirezionale

Supponiamo che un botanico voglia sapere se la crescita delle piante è influenzata dall’esposizione alla luce solare e dalla frequenza dell’irrigazione.

Pianta 40 semi e li lascia crescere per due mesi in diverse condizioni di esposizione al sole e frequenza di irrigazione. Dopo due mesi registra l’altezza di ogni pianta. I risultati sono mostrati sotto:

Nella tabella sopra vediamo che sono state coltivate cinque piante in ciascuna combinazione di condizioni.

Ad esempio, cinque piante sono state coltivate con irrigazione quotidiana e senza luce solare e la loro altezza dopo due mesi era di 4,8 pollici, 4,4 pollici, 3,2 pollici, 3,9 pollici e 4,4 pollici:

Esegue un’ANOVA bidirezionale in Excel e ottiene il seguente risultato:

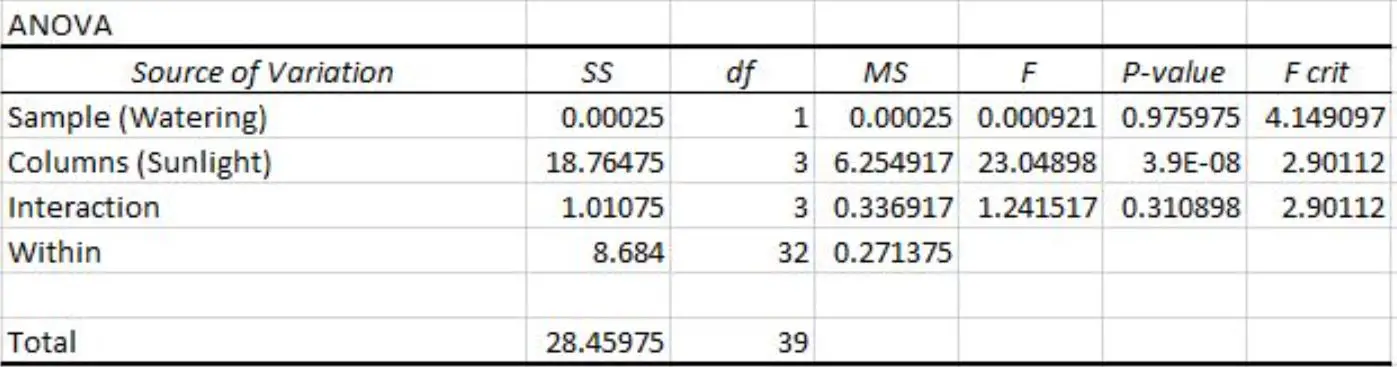
Possiamo vedere i seguenti valori p nel risultato della tabella ANOVA a due vie:

• Il valore p per la frequenza di irrigazione è 0,975975 . Questo non è statisticamente significativo al livello di significatività 0,05.
• Il valore p per l’esposizione al sole è 3,9E-8 (0,000000039) . Ciò è statisticamente significativo al livello di significatività 0,05.
• Il valore p per l’interazione tra la frequenza di irrigazione e l’esposizione al sole è 0,310898 . Questo non è statisticamente significativo al livello di significatività 0,05.

Questi risultati indicano che l’esposizione al sole è l’unico fattore con un effetto statisticamente significativo sull’altezza delle piante.

E poiché non vi è alcun effetto di interazione, l’effetto dell’esposizione al sole è coerente a ciascun livello di frequenza di irrigazione.

In poche parole, il fatto che una pianta venga annaffiata quotidianamente o settimanalmente non ha alcun impatto sul modo in cui l’esposizione al sole influisce sulla pianta.

Risorse addizionali

Le seguenti esercitazioni forniscono informazioni aggiuntive sui modelli ANOVA:

Come interpretare il valore F e il valore P in ANOVA
Come calcolare la somma dei quadrati in ANOVA
Cosa significa un valore F elevato in ANOVA?